課堂教學中“一題多變”的訓練策略研究
侯俊玲
摘 要 數學教學不但要教給學生數學知識,還應當培養學生多方面的素質能力。針對數學知識抽象、復雜的特點,通過引導學生進行數學知識的分析、理解,十分有助于發展學生的思維能力。在數學課堂教學中,進行“一題多變”訓練,能夠讓學生從多方面、多角度、多層次去理解數學概念,解決數學問題,發展數學思維。
關鍵詞 課堂教學;一題多變;訓練策略
中圖分類號:G424.21?? 文獻標識碼:A?????? 文章編號:1002-7661(2019)09-0148-01
數學教學主要依托于教材,其中有很多典型的習題、例子可以讓學生進行知識的理解、探索。教師在實際的教學過程中,應當對教材中的這些習題、例子加以重視,進行引申、拓展,使它們能夠充分為課堂教學服務。同時數學習題形式的多變也有助于吸引學生的好奇心以及學習興趣,培養起學生探索精神、創新思維、觀察能力、分析及解決數學問題的能力。根據數學知識形式多變的特點,教學中教師如果能夠有效的利用起“一題多變”教學法,將會極大提升數學教學質量。本文對“一題多變”訓練策略進行總結。
一、循序漸進,由淺入深
人們對客觀事物的認識都要經歷由簡單到復雜、由直觀到抽象的過程,通過表象逐漸看到本質。在數學課堂教學中,教師也應當遵循學生的知識認識規律,在評估學生知識理解能力、接受能力的基礎上,循序漸進進行誘導,讓學生通過自己的一步步努力能夠不斷實現新的突破,體驗成功的喜悅,從而越學越有動力。“一題多變”教學法則能實現激發學生數學興趣的目的。
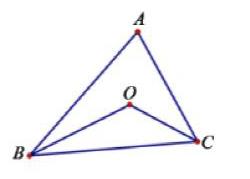
比如:我們在學習了與三角形有關的角的內容之后常會碰到這樣一個習題。
例如:在△ABC中,∠ACB=60°,∠ABC=50°,BO,CO分別平分∠ABC和∠ACB
求:∠BOC的度數
在處理這個習題時,同學們首先想到的就是在△BOC中利用內角和定理來求∠BOC,即:要求∠BOC,就要先求出∠OBC和∠OCB的度數,或求出∠OBC和∠OCB的度數和。學生在解決此問題后之后拋出變式一:將條件改為:∠ABC=45°,∠ACB=65°其它條件不變,求:∠BOC的度數。同樣方法學生可以結出結果,然后引導學生猜想猜想得出∠BOC的度數和三角形ABC的哪一個內角有關,有何關系?進而拋出變式二:探究∠BOC和∠A的度數關系。在處理該習題時采用的方法就是循序漸進,由表及里,符合學生認知規律。
二、由此及彼、類比思想
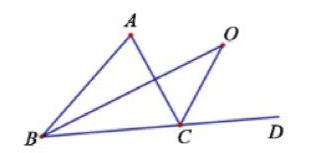
在解決了剛才的那個問題后,可以類比剛才的方法拋出變式進而拋出變式三:在△ABC中,∠ACB=60°,∠ABC=50°,BO,CO分別平分∠ABC和外角∠ACD。
求:∠BOC的度數
教師引導學生運用類比的思想解決該變式后,讓學生類比前面的自己給出組變式題目并嘗試解決總結規律。然后水到渠成的出現變式四、五。
變式四:將變式三條件中的∠ABC改為45°,∠ACB=65°其它條件不變。
求:∠BOC的度數
變式五:∠O和∠A的度數關系。解決此問題時,一直類比前面的變式題目進行。
三、變換圖形,總結歸納
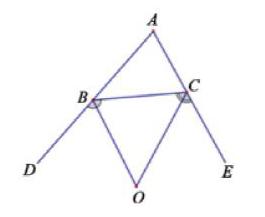
在解決了問題及幾個變式后,分析發現該變式題的問題是在例題的基礎上將兩個內角的平分線所形成的夾角角變為一內角及一外角的平分線所形成的夾角。那么:如果該為兩個外角的平分線的夾角會出現什么情況呢?讓學生畫出圖形來,結合圖形給出下面的幾個變式。
變式六:在△ABC中,∠ACB=60°,∠ABC=50°,BO,CO分別平分外角∠CBD和外角∠BCE。
求:∠BOC的度數
變式七:將變式六條件中的∠ABC改為45°,∠ACB=65°其它條件不變。
求:∠BOC的度數
變式八:探究變式六、七中∠BOC和∠A的度數關系
這樣本來一個題目,通過由表及里,由特殊到一般,舉一反三、類比運用,得出三個結論即∠O分別等于90°+∠A,∠A和90°—∠A。
總之,“一題多變”教學法能夠調動學生思維的靈活性、深入性,從改變圖形入手,只要能夠抓住圖形特點,便能由表及里、舉一反三,引導學生更深入的思考數學問題。
參考文獻:
[1]章美瓊.課堂教學中的“一題多變”策略研究[J].亞太教育,2016(18):43.

