讓圖形“說話”，給數(shù)學(xué)建模助力

雷清蘭

學(xué)生獲得知識(shí)的過程是一個(gè)漸悟與頓悟相結(jié)合的過程，在這個(gè)過程中，教師要適時(shí)地給予指導(dǎo)，在關(guān)鍵處為學(xué)生架梯、搭橋，使學(xué)生能夠有所感悟，能夠觸發(fā)思維的節(jié)點(diǎn)。小學(xué)生的抽象思維能力比較弱，在解決一些較為抽象的問題時(shí)離不開形象直觀的輔助性工具，如圖形、可視化多媒體課件等，教師在教學(xué)中需優(yōu)化教學(xué)手段并提供一些“媒介”來幫助學(xué)生解決難題。

一、重組圖形，助思維飛躍，構(gòu)建“歸一”模型

數(shù)學(xué)教學(xué)中，如果能夠引導(dǎo)學(xué)生在思考問題時(shí)思維“向前一步”，稍微“改變”一點(diǎn)點(diǎn)，往往能夠起到事半功倍的作用。而這“向前一步”，恰好為學(xué)生抽象思維的發(fā)展搭橋鋪路，為學(xué)生成功建模助力。

北師大版三年級(jí)《數(shù)學(xué)》下冊(cè)第17頁(yè)，教學(xué)內(nèi)容“買新書”（用“歸一法”解決問題），其情景問題是“200本書放在兩個(gè)書架上（每個(gè)書架有4層），平均每個(gè)書架每層放多少本書？”

淘氣的方法是先求每個(gè)書架放多少本書，列式200÷2=100（本），再求每層放多少本書，列式100÷4=25（本）。

笑笑的方法是先求兩個(gè)書架一共有幾層，列式2×4=8（層），再求每層放多少本書，列式200÷8=25（本）。對(duì)三年級(jí)的學(xué)生來說，要理解笑笑的方法，僅有教材的情景圖是不夠的，還需要教師對(duì)圖形稍作優(yōu)化。

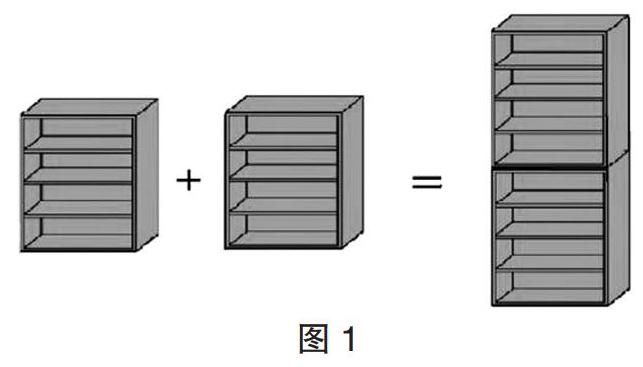
可在課本情景圖的基礎(chǔ)上，把圖形稍作改變，讓兩個(gè)書架疊放起來，如圖1所示。既出示課本的情景圖，又出示疊加的書架圖，這樣對(duì)學(xué)生理解笑笑的解答方法200÷（2×4），會(huì)有很大的幫助。為什么要先把2×4算出來？看到圖1中兩個(gè)疊起來的柜子，學(xué)生一下子就“恍然大悟”。柜子疊起來后，直觀的圖形告訴學(xué)生，兩個(gè)書架一共有（2×4）層書柜，所以要求每層能夠放多少本書，可以直接列式：200÷（2×4）。

我們不要小看這會(huì)“說話”的書架圖，實(shí)際上是讓學(xué)生的思維邁了一大步，對(duì)“歸一”問題的另類解法進(jìn)行了恰如其分的數(shù)學(xué)建模。毫不夸張地說，學(xué)生理解好了這一環(huán)節(jié)，以后解決這類“歸一”問題時(shí)便能得心應(yīng)手了。

在教學(xué)中，教師要善于把握這樣的契機(jī)，運(yùn)用數(shù)形結(jié)合思想優(yōu)化圖形，促成學(xué)生思維的飛躍。

二、添加“方塊”，助數(shù)感建立，構(gòu)建豎式模型

一年級(jí)學(xué)生的數(shù)學(xué)學(xué)習(xí)，很大程度上需借助肢體動(dòng)作。他們?cè)趯W(xué)習(xí)簡(jiǎn)單計(jì)數(shù)和加減法的時(shí)候，往往借助數(shù)手指、擺小棒、擺小方塊等操作來建立形象思維。

在數(shù)的學(xué)習(xí)中，主要通過數(shù)數(shù)、計(jì)數(shù)、計(jì)算讓學(xué)生逐步建立數(shù)感，從而能夠理解現(xiàn)實(shí)生活中數(shù)的意義，表述具體情境中的數(shù)量關(guān)系。對(duì)于低年級(jí)的學(xué)生來說，建立數(shù)感的方法主要是依靠教師去引導(dǎo)的動(dòng)手操作，如畫圖、用實(shí)物模擬數(shù)的場(chǎng)景等，并運(yùn)用數(shù)形結(jié)合思想來進(jìn)行數(shù)的學(xué)習(xí)，促進(jìn)數(shù)感的建立。

如在教授北師大版一年級(jí)《數(shù)學(xué)》下冊(cè)“百以內(nèi)的進(jìn)位加法”時(shí)，可以借助圖2幫助學(xué)生理解。在圖2中，如果只有上邊的小方塊，學(xué)生的學(xué)習(xí)意識(shí)往往停留在“動(dòng)作”上，難以上升為“思維”;如果只有下邊的豎式，學(xué)生看到的是“單調(diào)”的數(shù)和抽象的豎式，也難以形成自己的“數(shù)感”，難以發(fā)展數(shù)形結(jié)合的思想和口算能力。可以說，圖2上邊的小方塊與下邊的豎式是相輔相成的，對(duì)學(xué)生認(rèn)知能力的提升、思維發(fā)展等，都有較大的幫助（圖2借鑒了臺(tái)灣地區(qū)教材“小學(xué)課本100學(xué)年第3冊(cè)”第19頁(yè)的部分內(nèi)容）。

對(duì)于一年級(jí)的學(xué)生而言，豎式是“新鮮事物”，在學(xué)習(xí)豎式的時(shí)候，可以借助常用的計(jì)數(shù)工具——小棒或者小方塊。只有找到了學(xué)生的認(rèn)知起點(diǎn)，有了形象的圖形做參照物，學(xué)生對(duì)豎式的領(lǐng)會(huì)與把握才會(huì)水到渠成。同時(shí)，也有助于數(shù)感的建立、直觀思維向抽象思維的發(fā)展，以及由直觀圖形到豎式計(jì)算的建模。

三、漸變圖形，行轉(zhuǎn)化之妙，構(gòu)建“柱體”模型

圖形面積、體積的計(jì)算，一方面是用面積單位或體積單位去度量物體的面積或體積，從而得出物體面積或者體積的大小;另一方面，是通過轉(zhuǎn)化的數(shù)學(xué)思想去推導(dǎo)幾何形體的面積或者體積的計(jì)算方法。“度量”只是認(rèn)知思維的第一步，真正要讓學(xué)生理解領(lǐng)會(huì)的是，通過轉(zhuǎn)化的數(shù)學(xué)思想、運(yùn)用等積變形的數(shù)學(xué)規(guī)律，掌握一種解決問題的思路、方法與策略。

我們的教材，在推導(dǎo)圓柱體體積的計(jì)算公式時(shí)，普遍是把圓柱沿高切割成若干等份后，拼成一個(gè)近似的長(zhǎng)方體，然后由近似長(zhǎng)方體的體積推導(dǎo)出圓柱體體積。這樣的推導(dǎo)運(yùn)用了知識(shí)的遷移思維：圓面積的計(jì)算公式是把圓變成近似長(zhǎng)方形進(jìn)行推導(dǎo)的;同理，圓柱體體積計(jì)算公式則把它變成近似的長(zhǎng)方體進(jìn)行推導(dǎo)。

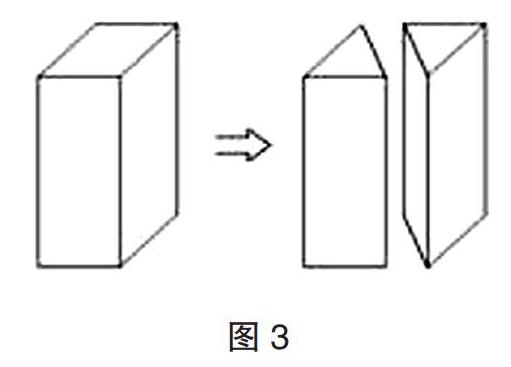
其實(shí)，推導(dǎo)圓柱體體積計(jì)算公式，我們還可以運(yùn)用“漸變”的極限思想。五年級(jí)的學(xué)生已經(jīng)學(xué)習(xí)了長(zhǎng)方體體積計(jì)算公式，知道長(zhǎng)方體體積=底面積×高，以此類推，圖3中的一個(gè)三棱柱的體積=1/2長(zhǎng)方體體積=1/2×長(zhǎng)方體底面積×高=三棱柱底面積×高。

在學(xué)生觀察圖4 的過程中，教師要注意引導(dǎo)學(xué)生去思考：三棱柱的體積=底面積×高，長(zhǎng)方體（四棱柱）體積=底面積×高，通過底面的虛線可以看出，五棱柱能夠分割成三個(gè)三棱柱，故可以推出其體積也是等于底面積×高。接著再讓學(xué)生展開想象，當(dāng)柱體的底面邊數(shù)無限多的時(shí)候，多棱柱也會(huì)漸漸變成圓柱體。從這個(gè)角度就可以較容易地引導(dǎo)學(xué)生推導(dǎo)出圓柱體體積的計(jì)算公式為底面積乘以高。

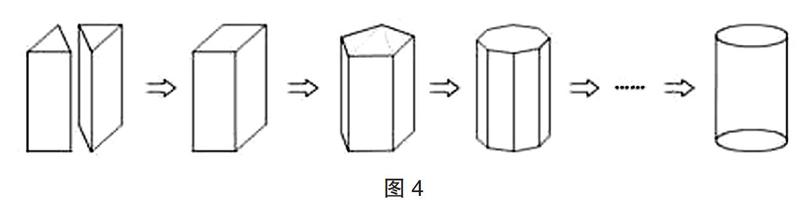
圖4的系列組圖，可以“悄悄”地“告訴”學(xué)生圓柱是怎樣“成長(zhǎng)”的，圓柱的體積經(jīng)歷了怎樣的“變化過程”。這樣，教師借助直觀圖形，在學(xué)生的頭腦中滲透了漸變、極限、轉(zhuǎn)化等數(shù)學(xué)思想方法，并教會(huì)他們運(yùn)用這些方法構(gòu)建圓柱體體積計(jì)算方法的數(shù)學(xué)模型。

總之，數(shù)學(xué)學(xué)習(xí)主要是發(fā)展學(xué)生的數(shù)學(xué)思維，為學(xué)生提供解決問題的方法，為學(xué)生的建模提供思路和參考。數(shù)學(xué)知識(shí)的學(xué)習(xí)，其實(shí)就是建模的學(xué)習(xí)。因此，無論是為了學(xué)生抽象思維的形成與發(fā)展，還是指導(dǎo)學(xué)生進(jìn)行數(shù)學(xué)建模，都需要教師優(yōu)化教學(xué)“媒介”，為他們發(fā)展數(shù)學(xué)核心素養(yǎng)搭橋鋪路。

責(zé)任編輯 羅 峰

實(shí)習(xí)編輯 蔡李鈺