基于數(shù)學基本活動經(jīng)驗積累的教學研究

顧君

[摘? 要] 文章以“三角尺拼角”一課為例，進行了有效積累數(shù)學基本活動經(jīng)驗途徑的教學研究. 筆者基于數(shù)學基本活動經(jīng)驗積累的課堂教學實踐與思考，從四個層面來探究數(shù)學實驗在初中數(shù)學課堂教學中的活動經(jīng)驗積累.

[關(guān)鍵詞] 數(shù)學基本活動經(jīng)驗;數(shù)學實驗;三角尺拼角

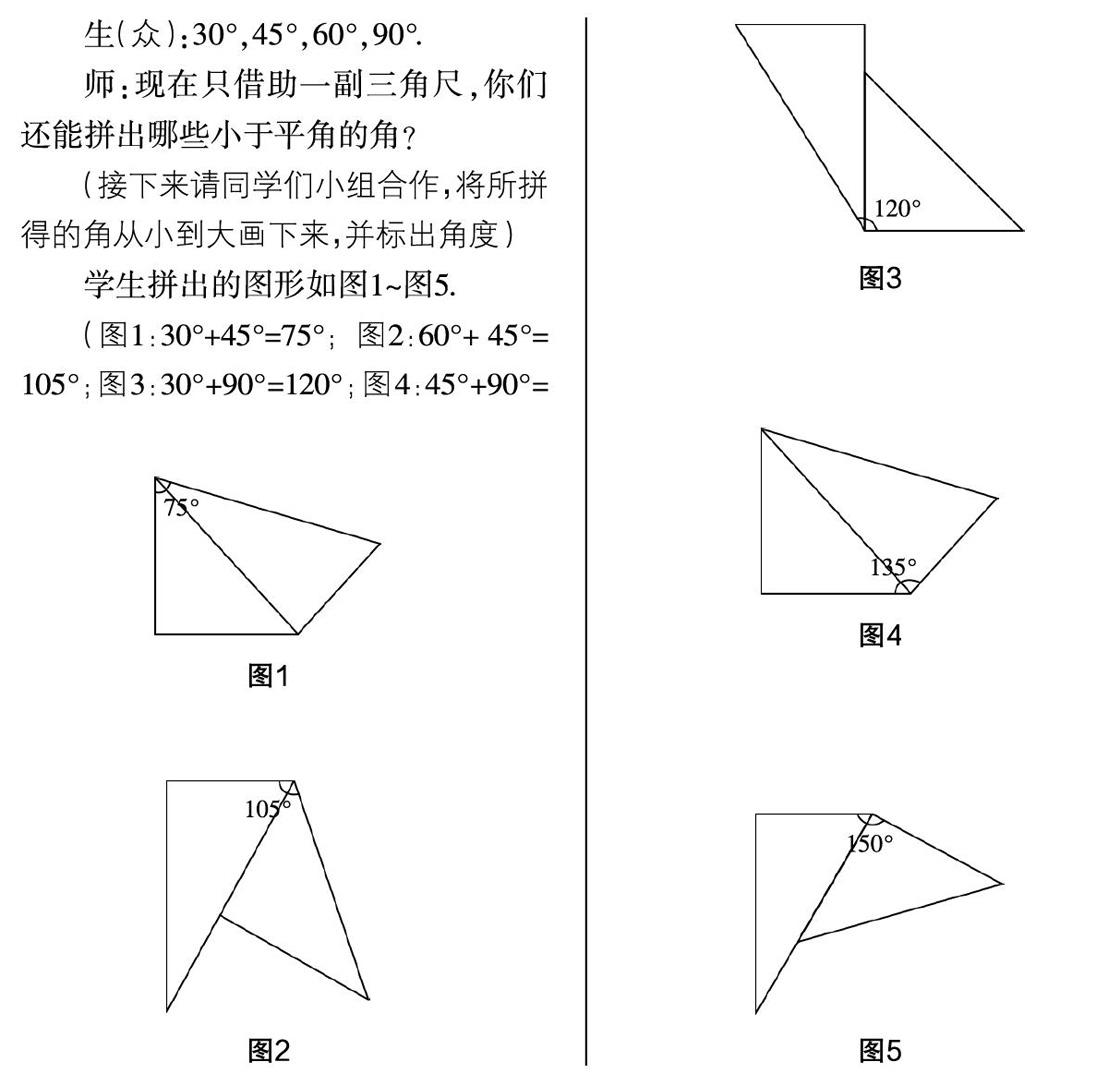
數(shù)學基本活動經(jīng)驗既是學生在數(shù)學活動中直接獲得的經(jīng)驗，也是學生在不斷思考和反復探究之后提煉的個人認知，其最高層次為形成數(shù)學的直觀能力. 因此，幫助學生積累數(shù)學基本活動經(jīng)驗是教師進行教學的重要目標之一. 而數(shù)學實驗作為積累數(shù)學基本活動經(jīng)驗的有效載體，近年來已成為一個熱門的研究話題. 筆者以七上《初中數(shù)學實驗手冊》中的“三角尺拼角”一課為例，從經(jīng)驗激活、經(jīng)驗積累、經(jīng)驗遷移和經(jīng)驗升華四個層面來探究數(shù)學實驗在初中數(shù)學課堂教學中活動經(jīng)驗積累的設(shè)計與思考.

師：這位同學講得非常好. 用三角尺拼角包含兩種方法，一種是“拼”，另一種是“疊”. 這里的“拼”就是數(shù)學上的“補”，“疊”就是“割”，合起來就是“割補”. 那我們?nèi)绾纹矗拍苁菇Y(jié)果既不重復又不遺漏呢？

生3：可以先固定一塊三角板的一個角，然后用另一塊三角板的角去拼.

師：這位同學是從拼三角尺——“形”的角度來分析的. 那還有其他的方法嗎？

生4：可以將兩塊三角板的角度進行“加”或者“減”.

設(shè)計意圖對于活動1，學生通過對三角尺已有角的認識，激活了已有知識經(jīng)驗，為積累更高層次的活動經(jīng)驗做準備. 此階段學生對角的認識是直觀的、未經(jīng)提煉的、與操作緊密相關(guān)的淺層次活動經(jīng)驗. 此時，教師可引導學生對已有經(jīng)驗進行觀察、猜想、歸納和內(nèi)化，形成較有條理的數(shù)學活動經(jīng)驗：①割補思想：“拼”與“疊”對應幾何中的“補”與“割”. ②數(shù)形結(jié)合思想：“拼”與“疊”的過程對應著角度之間的“加”與“減”. ③拼角有兩種方法：一種是從圖形上來研究;另一種是從角度上來研究. “拼角”的本質(zhì)是“拼角度”.

2. 兩副三角尺拼角：積累活動經(jīng)驗

活動2的教學片段如下.

師：接下來，用兩副三角尺，我們還能拼得哪些角呢？

生1：如圖7.

師：如果用三副三角尺，還能得到其他的角嗎？

生（眾）：不能.

師：觀察三角尺所拼得的這些角，它們之間有何共同特點？

生（眾）：角度都是15°的整數(shù)倍.

師：如果將15°作為一個模板，那么0°～180°之間15°的整數(shù)倍角都可以由此模板畫出.

設(shè)計意圖學生在活動2中進行了思考、總結(jié)和內(nèi)化，積累了相關(guān)的活動經(jīng)驗，但是系統(tǒng)的經(jīng)驗很難在一次操作過程中獲得. 假如經(jīng)歷多次反復操作、探究過程，學生會對已有的活動經(jīng)驗進行再積累和完善，從而逐漸形成概括性的經(jīng)驗：①用兩副三角尺拼角，還可以拼出一個新的角度——165°，但用三副或多副三角尺進行拼角，并不能拼得其他角度;②從結(jié)果上分析，發(fā)現(xiàn)拼得的角都具備共同的特征——均為15°的整數(shù)倍角，因此將15°作為模板能畫出15°的整數(shù)倍角.

3. 借助模板畫角：遷移活動經(jīng)驗

活動3的教學片段如下.

數(shù)學活動經(jīng)驗的遷移能力是學生的一種創(chuàng)新能力，即在原有活動經(jīng)驗的基礎(chǔ)上再次遇到類似的情景，將已有數(shù)學活動經(jīng)驗遷移應用于類似情景，產(chǎn)生新的認識經(jīng)驗，按照這種模式，重復使用這種經(jīng)驗，形成系統(tǒng)的經(jīng)驗. 活動3用含17°和19°的模板，通過活動經(jīng)驗的遷移，發(fā)現(xiàn)不僅能畫出偶數(shù)角，還能畫出奇數(shù)角. 此時，教師引導學生思考畫出的角度和給定模板之間的關(guān)系，歸納出“15是30和45的最大公因數(shù)，1是17和19的最大公因數(shù)”. 由特殊情況推廣到一般，即給定兩個角的模板，求兩個角的度數(shù)的最大公因數(shù)，以這個最大公因數(shù)的角度作為新的模板，可以畫出其任意整數(shù)倍角，這個過程就是“經(jīng)驗遷移”的過程.

4. 畫角方案設(shè)計：升華活動經(jīng)驗

活動4的教學片段如下.

設(shè)計意圖經(jīng)歷前面活動經(jīng)驗的激活、積累和遷移，活動4是對此前積累的活動經(jīng)驗的應用和升華. 如果給定m°和n°的模板，本質(zhì)上是求這兩個度數(shù)（m和n）的最大公因數(shù)，所畫出的角就是這兩個度數(shù)的最大公因數(shù)的整數(shù)倍角. 由此，如果給定3個角、4個角乃至多個角的模板，通過角度之間的加減與倍數(shù)關(guān)系，所能畫得的角就是這些角的最大公因數(shù)的整數(shù)倍角. 教師通過引導，將學生已有的數(shù)學活動經(jīng)驗進行升華，長此以往，形成數(shù)學直觀.

1. 經(jīng)歷經(jīng)驗激活到經(jīng)驗升華，積累實踐活動經(jīng)驗

實踐經(jīng)驗主要是從客觀世界中抽象出來的，是通過動手操作從數(shù)學活動中獲得經(jīng)驗，并將所獲的相關(guān)經(jīng)驗應用于解決實際問題. 在整個活動過程中，學生根據(jù)已有對角的認知，激活了原有的經(jīng)驗. 學生還在反復操作活動過程中歸納、思考和內(nèi)化，形成了概括性的經(jīng)驗，發(fā)現(xiàn)了三角尺拼角的一般規(guī)律. 教師則通過引導學生將已有活動經(jīng)驗遷移到類似的問題中，以解決模板畫角問題，并對之前所獲得的一般性規(guī)律進行推廣和總結(jié). 這種學習方式，不是讓學生被動接受教科書上的現(xiàn)成結(jié)論，而是鼓勵學生從自己已有的“數(shù)學經(jīng)驗”出發(fā)，變“聽數(shù)學”為“做數(shù)學”，變“看演示”為“動手操作”，變“機械接受”為“主動探究”，培養(yǎng)學生的動手操作能力、解決問題的能力和創(chuàng)新精神，積累實踐活動經(jīng)驗.

2. 經(jīng)歷無序認識到有序認知，積累思維活動經(jīng)驗

思維活動經(jīng)驗是將實際問題進行數(shù)學化和符號化，并在符號化的過程中積累活動經(jīng)驗. 從認識的過程來說，直觀感受是在事物的作用下，學生在頭腦中形成的感性知識. 盡管直觀感受只能形成感性知識，但它卻是思維的起點，是感性知識轉(zhuǎn)化為理性認知的開端. 學生在本實驗中已有的認識是三角尺本身具備的一些特征，此類經(jīng)驗很大一部分是數(shù)學活動現(xiàn)象或者直觀結(jié)果，是比較粗糙、模糊和無序的認識，受個人的主觀意識和活動情景影響比較大. 學生在思維層面通過思考，發(fā)現(xiàn)其實“拼角”就是在“拼角度”，“拼角”是操作層面的認識，而“拼角度”已經(jīng)上升到了思維層面，角度的加減或者倍數(shù)關(guān)系是拼角的符號化表達. 因此，在用模板畫角的過程中，從操作層面理解已經(jīng)有所局限，此時需要從思維層面進行再認識，通過歸納總結(jié)得到結(jié)論. 學生在探究活動過程中從無序的結(jié)果入手，經(jīng)過探究、思考、歸納和內(nèi)化，形成思維上的有序認知，并積累思維活動經(jīng)驗.

本節(jié)課從特殊入手，嘗試探索、歸納一般規(guī)律或結(jié)論，借助演繹推理驗證一般規(guī)律. 這個過程能讓學生感悟數(shù)學基本活動經(jīng)驗積累的思維模式，長此以往，能形成數(shù)學直觀，達到數(shù)學基本活動經(jīng)驗積累的最高層次.