分層走班是一道靚麗的風景線

丁同軍

[摘? 要] 分層走班教學符合新課改的發展要求，體現了因材施教、以人為本的教學原則. 分層教學充分認識差異、尊重差異、研究差異，并針對不同層次的學生進行分層備課、分層教學、分層命題、分層作業、分層輔導……能真正提高課堂效率.

[關鍵詞] 目標分層;教學分層;作業分層;輔導分層

古人云“孔子教人，各因其材”，指的是教學應從學生的個性特點出發，有的放矢地進行差異化教學，以使每個學生都能得到最佳發展[1]. 隨著數學的難度逐漸增大，優生吃不飽、差生吃不了的問題日益突出，于是我們進行了分層走班教學初探.

基礎扎實，學習能力突出的尖子生劃為A班;基礎一般，學習能力不突出的中等生劃為B班;基礎欠缺，學習能力較差的后進生劃為C班. 對目標進行分層：A班除了完成“課標”規定的教學任務之外，還需在深度上挖掘，在廣度上拓展，加強能力培養;B班要立足課本，夯實基礎，注重知識、技能的訓練;對于C班的教學，則要強化學法指導，培養學生的興趣，樹立學生的信心.

案例1? ? ?九年級數學“垂徑定理”的目標分層設計.

從知識、技能、能力和思想方法等方面提出分層要求：A班學生在充分理解、掌握垂徑定理的基礎上，會靈活應用定理解決問題，讓學生經歷“實驗—觀察—猜想—驗證—歸納”的研究過程，培養學生動手實踐、觀察分析、歸納問題和解決問題的能力，灌輸勇于探索的精神;B班學生在理解、掌握垂徑定理的基礎上，靈活運用定理解決問題，通過圓的軸對稱性探究圓的相關性質，進一步體會和理解研究幾何圖形的方法，培養學生實事求是的科學態度和積極主動的參與精神;C班學生理解勾股定理并基本掌握垂徑定理，能應用垂徑定理解決簡單的問題，讓學生動手、動口、動眼、動腦，培養學生的能力，激發學生的求知欲，讓學生感受數學與生活的緊密聯系.

課堂教學是分層教學的主陣地，是決定分層成敗的關鍵. 教師應深入研究教材教法、學生學情，精心設計不同層次的課堂. A班的教學要少干涉多放手，讓學生在獨立探究和合作交流中學習;B班的教學則要緊扣基礎，強化能力訓練，培養良好的學習習慣;C班的教學需低起點、低要求，不違背規律，不揠苗助長.

案例2八年級數學“全等三角形的判定”教學分層設計.

C班按照“課標”要求分5個課時按部就班地教學. A班則把四個定理放在同一課時中呈現，利用問題“一塊三角形玻璃摔成兩塊，帶哪一塊去配和原來一樣的三角形玻璃”引出新課，誘導學生分析判斷兩個三角形全等的條件. 從三邊三角的元素中選3個，其中有4種情況可以判定兩個三角形全等，進而歸納出全等三角形的4個判定定理. 還要求A班學生能辨別“AAA”和“SSA”不一定能證明兩個三角形全等. 最后通過2節習題課鞏固、提高. 這樣的設計，3節課就完成了5節課的任務，既提高了課堂效率，又增強了知識之間的聯系. B班學生的水平介于A班和C班之間，教師可以根據需要把A班或C班的成功經驗推廣到B班教學中.

為了鞏固和延續課堂教學效果，作業也要分層：基礎性作業主要針對的是后進生，考查基本概念、公式、性質等，以鞏固基礎、培養習慣為目的;提高性作業主要針對的是中等生，以能力發展、拓展延伸類試題為主，訓練解題素質;創新性作業主要針對的是優生，以中上難度題為主，培養綜合思維能力.

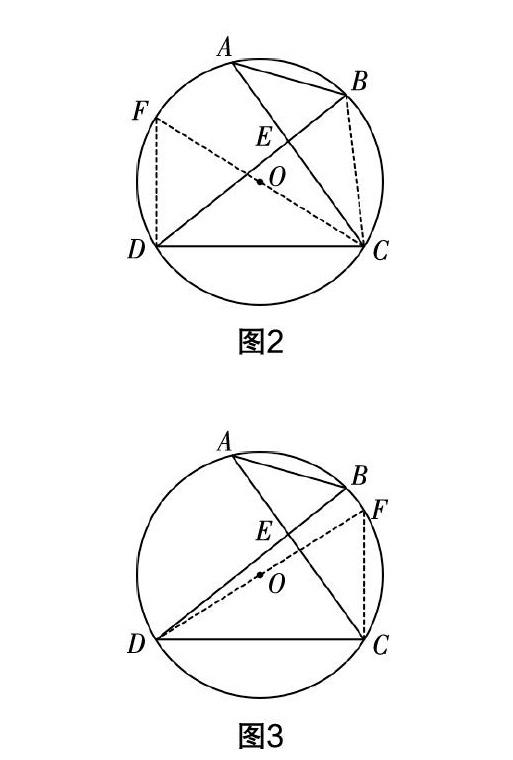
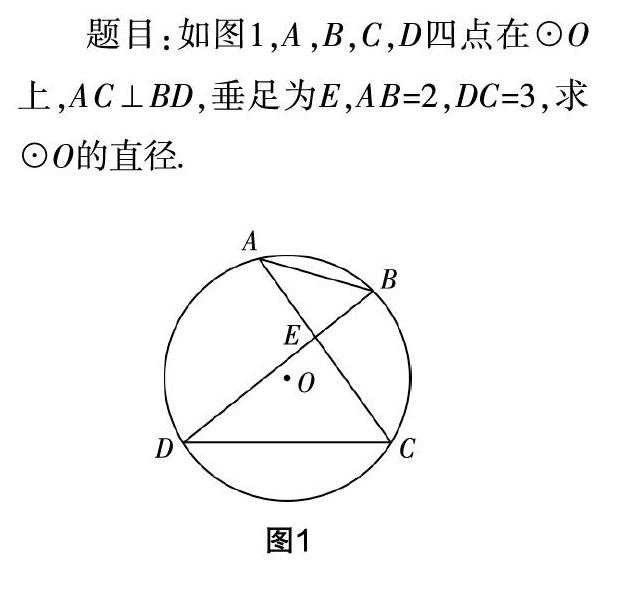
分析題目：本題主要考查圓周角定理、勾股定理等知識.

分層輔導：（1）對A班學生的輔導：A班學生的解題能力強，教師應放手讓學生自主學習，并適當提示. 本題由問題引出，讓學生探索輔助線的作法——如圖2的CF或圖3的DF，構造Rt△CDF. 圖2由圓周角定理知∠F=∠DBC，再利用等角的余角相等得∠FCD =∠BCA，從而推出DF=AB=2. 同理，可得圖3中的弦FC=AB=2，最后可用勾股定理求出直徑.（2）對B班學生的輔導：對于B班的學生，教師應給予更多的幫助，應預設解題鋪墊，讓學生拾階而上. 可運用分析法引導學生添加直徑，如圖2中的CF或圖3中的DF，構造出Rt△CDF，再利用圓周角定理推出DF=AB=2（圖2），最后用勾股定理算出直徑. 如果時間允許，可讓B班學生和A班學生一樣，嘗試添加圖3中的輔助線來求解. （3）對C班學生的輔導：C班學生解這道題難度較大，需做到以下幾點：①由易到難，先預先鋪墊好本題相關的知識點，增設過渡學習的緩沖區;②循循善誘，切勿急于求成，可從添加輔助線的方法到圓周角定理推出弦長，最后通過勾股定理求出直徑;③及時鼓勵，要善于發現學生的閃光點并及時給予表揚;④題后小結，解題后要及時歸納方法，形成經驗.

今后，我們將繼續開展分層走班研究，不斷地改進分層走班教學，讓分層走班成為校園中一道靚麗的風景線.

參考文獻：

[1]李庾南. 自學·議論·引導教學論[M]. 北京：人民教育出版社，2013（7）.

[2]李庾南，陳育彬. 中學數學新課程教學設計30例——學力是這樣發展的[M]. 北京：人民教育出版社，2007.