論初中數學文本閱讀的方法與策略

黃萍萍

[摘? 要] 數學文本閱讀是學生依據自身已有知識經驗，通過閱讀建構數學意義以及數學方法的一種學習活動. 文章認為可以通過以下方式培養初中學生數學文本閱讀能力：精讀“連續文本”“非連續文本”;在“主干”指引中整合，促進精讀;在轉化中建構關聯，促進深度閱讀.

[關鍵詞] 連續文本;非連續文本;文本閱讀

閱讀指導在數學教學中發揮著極其重要的作用. 教師的閱讀指導越充分，學生的閱讀能力就越強，進而理解數學問題就越高效，思維能力就越強. 因此，數學教師應注重對學生閱讀數學文本能力的培養.

數學是遵循一定的規則去表達數學思想和數學意義的學科，其中符號、圖形以及圖表在數學學科中占據著主導地位. 那么，教師應采用哪些方式去指導學生進行數學文本閱讀呢？筆者結合教學與實踐，從以下幾點談談自身的一些思考.

精讀“連續文本”

所謂的“連續文本”，就是指句子和段落結合組成的完整的數學文本. 由于它具有完整性，學生在查找數學信息時需對句子中的基本元素進行分析篩選，進而獲取自己需要的數學信息. 比如數學中的定義、定理等，皆是通過“連續文本”的形式表現出來的.

1. 或添或刪，變通句式

數學文本中存在著一些專用的名詞或不連續句式，由于其本身的特點，學生在學習時往往會比較吃力. 此時若是能變通句式，或添或刪，使句式完善易懂，那閱讀過程自然就暢通無阻了，數學思路自然也就形成了.

案例1以“角平分線性質的逆定理”為例.

教材中的命題是這樣的：“到角兩邊距離相等的點在這個角的平分線上.” 我們可以進行如下的轉換：“假如有一個點，它到一個角兩邊的距離相等，那就是說這個點在這個角的平分線上.” 經過這樣的轉換，變成了條件和結論明確的句式，學生在理解時就順暢多了. 倘若再以圖形配之，用符號語言來替代文字表述的形式，理解起來就更為容易了.

借助這種方法，在彰顯數學定理嚴密、精煉的同時，還可使數學語言更具魅力. 教師可以適當鼓勵學生借助簡潔精確的語言來理解數學內容.

2. 斟酌推敲，理解句式

學生需斟酌推敲，才能透徹理解數學用詞的深刻含義，進而形成準確的解題思路. 語文課堂中，可以借助“反義詞”引導學生透徹理解一些事物，數學教學中，也可以巧妙運用這些方法，提升教學效果.

筆者在進行作業批改時，發現一些學生將0.27，填入了下一個集合中. 他們認為“非負整數”即為不是“負整數”. 基于此，筆者引導學生進行如下的操作：①先將“的”字加在“非負整數集合”中，而后思考現在集合中該怎么填;②請思考“非負整數”與“正整數”兩個概念的異同點. 在“非負整數”加上“的”之后可以有以下兩種說法：一種為“非負的整數”，另一種為“非的負整數”. 如果“正整數”中的“正”是用來修飾“整數”的，那么“非負整數”中的“非負”也一樣是用來修飾“整數”的. 因此，“非負整數”就可以轉變為“非負的整數”. 據此理解，很容易就得出了答案.

3. 刨根問底，完善句式

數學中，一些概念通過符號的形式進行描述. 由于這些符號較為抽象，學生頓感生疏，學起來容易產生畏難心理;還有一些學生無法透徹理解概念括號內條件的內涵，造成理解的偏差.

案例3以“一元二次方程的概念”為例.

精讀“非連續文本”

所謂“非連續文本”，就是將數學內容借助數據表格、圖表和曲線圖等方法進行表述. 在數學課堂中，滲透“非連續文本”可以讓教學內容更為清晰，提升學生思維能力.

1. 追根溯源，依次對號

掌握簡潔的數學符號可以方便書寫、運算以及推理. 筆者引導學生實現符號語言到數學文本的轉化，從而加深對他們符號文本的理解，進而探究問題的本質，更好地解決問題.

分析? 借助文字語言分別表述等號兩邊的字母符號，串聯成句子：“某個數的絕對值就等于這個數”，這樣一來，學生就可以清楚找出問題的答案，并進行解答.

2. 或涂或畫，剖析圖形

“圖形文本”具有直觀性，方便觀察和賦予想象. 因此，教師需引導學生“破解”圖形文本，進而形成思維策略. 筆者認為，可以從以下幾個方面進行引導：

（1）借助“標識”. 如圖1所示，相等的角可以用相同的“標識”表現，相等的線段可以用一樣的“標識”體現，這樣學生觀察起來就便捷多了，分析起來也更為透徹.

（2）借助“填色”. 在復雜圖形中，我們可以借助“填色”，標出所需探究的部分，這樣有助于學生觀察，避免其他部分的干擾.

案例5以“判斷平行四邊形”為例.

在“主干”指引中整合，促進?精讀

學生在解決數學問題時，通常會遇到一些以文字、符號、圖表共同表述的題型. 解決此類問題，教師應引導學生注重主體要素，分整相結合，透徹理解閱讀.

案例6以“分類討論建立函數解析式”為例.

分析? 此案例中，牽涉到諸多變量之間的關聯，筆者要求學生從以下五個部分著手：“運動的狀態”“運動之后的圖形變化”“需求面積”“面積的函數關系式”“函數的圖像”，根據這些進行填表，并解答. 盡管此題中沒有要求用函數圖像的方法進行解答，但是借助圖形可以清晰表述各變量之間的內在關聯. 從圖中可看出，點P和點Q在圖形邊上的運動狀態，可以映射出三種函數關系式，從中可以感悟分類思想. 將圖像合并，展現點P和點Q在運動之后△BPQ面積的變化. 這個過程中經過不斷整合讀題，單一知識分析，借助圖表，先分后合，整體推進，進而獲取解題途徑.

在轉化中建構關聯，促進深度閱讀

在數學學習中，教師可以轉化各類文本，借助比較建構內部關聯，能夠有效而快速地促進學生理解，引導學生正確運用. 在教學“函數概念”這一內容時，基于學生對其的初步認識，筆者引導學生探究表述函數的各類數學文本之間的關聯，讓其對函數形成更深層次的理解和認知，進而不斷優化思維，提升分析問題和解決問題的能力.

案例7以“數學文本形式的轉化”為例.

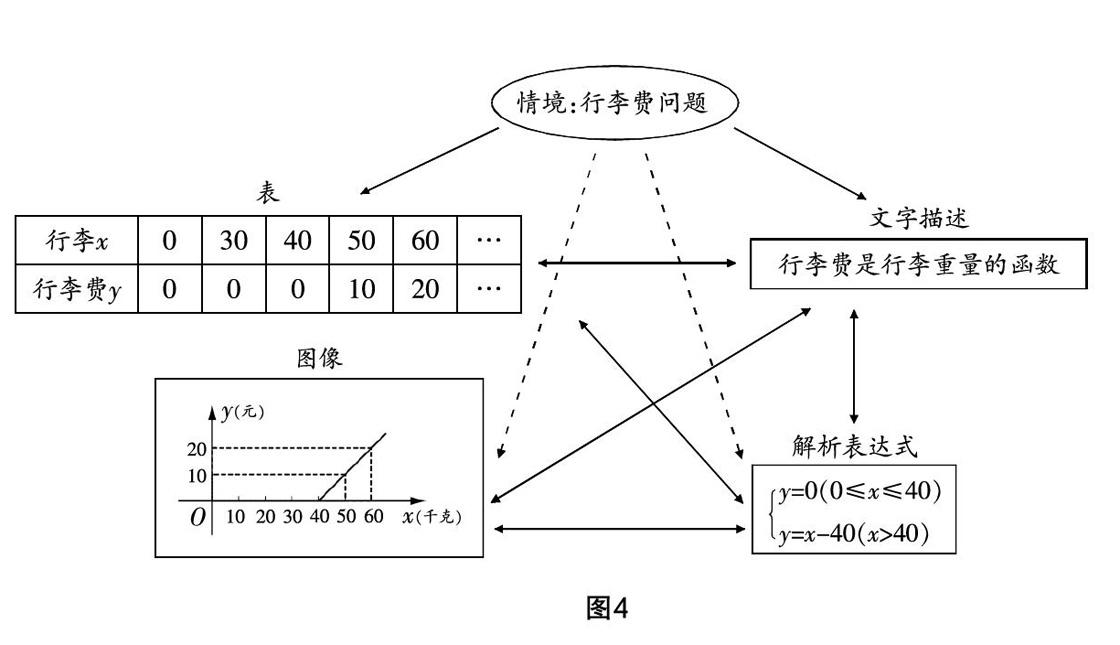
如圖4，關于行李費問題.

此情境中的函數，采用了4種數學文本的形式進行表述. 借助“表”，簡潔明了地把兩集合中的元素依次對應;借助“文字描述”，表述兩個量之間的關聯;借助“圖像”，合理轉化元素為直角坐標系中的點;借助“解析表達式”，運用數字符號表述每對數對的法則. 這四種形式從多個角度探究函數，各自具有不同的優勢. 學生可根據自身的喜好和需求進行選擇，體現了閱讀方式的廣闊性. 在進行函數學習的過程中，多采用這種方式滲透閱讀，能幫助學生從多角度、以多種方式分析和解決問題.

總之，閱讀能力的高低，直接影響著學生的學習效率[2]. 筆者經過嘗試，借助閱讀這一工具，不斷引導學生積累閱讀經驗，培養其數學學習能力，提升學生的數學思維水平，進而提升學生的數學核心素養.

參考文獻：

[1]李祎，曹益華.概念的本質與定義方式探究[J].數學教育學報，2013，22（6）：5-8.

[2]田麗霞.用文化浸潤心靈，讓閱讀伴隨成長[J].班主任，2015（1）：64-67.