集合易錯題歸類剖析

■河南省太康縣第一高級中學

集合是高考的必考知識點,往往在第一題的位置,從內容上看,主要以考查概念和計算為主,考查集合的交、并、補運算;從題型上看,往往以選擇題、填空題的形式出現,常與不等式、函數等知識交匯考查,解決此類問題時首先要明確集合中的元素,理解基本概念、基本運算,可以借助數軸或者V e n n圖直觀理解。

關于該部分知識,同學們的易錯點主要有:①容易忽視空集的情況;②集合的表示方法,如不等式的解集必須用集合或者區間表示,不能用不等式比表示。

例1 設集合A={x|a x2-a x+1＜0},若A=?,則實數a的取值集合是( )。

易錯分析：此題容易忽視a=0的情況,題目中并沒有說是一元二次不等式。

解：當a=0時,A=?;

綜上所述,a的取值范圍為[0,4]。故選D。

例2 已知集合M=,則( )。

易錯分析：不會化簡,感覺無從下手,找不到兩個集合之間的聯系與區別導致出錯。

解：集合

因為k+2(k∈Z)為整數,而2k+1(k∈Z)為奇數,所以集合M、N的關系為N?M。故選C。

例3 已知集合A={x|log2x＞1},B={x|x2-4x-5≤0},則B∩?RA=( )。

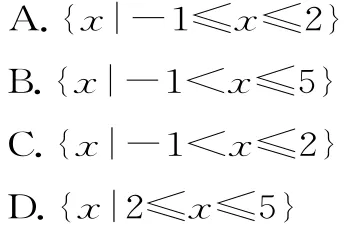
易錯分析：在解決不等式與集合的交、并、補集運算的時候,區間的開閉是學生最容易出錯的地方,一定要注意端點值的取舍。

解：A={x|log2x＞1}={x|x＞2},B={x|x2-4x-5≤0}={x|-1≤x≤5},則?RA={x|x≤2},B∩?RA={x|-1≤x≤2}。故選A。

例4 設集合A={x2-3x+2=0},B={x2-a x+2=0},若A∪B=A,求由a的值組成的集合。

易錯分析：解答本題的常見錯誤是:①未能通過檢驗剔除a=±2 2;②遺漏B=?的情況,應注意解題時空集優先的原則。

解：由A∪B=A,可知B?A,而A={1,2},故B可為{1,2},{1},{2},?。

當B={1,2}=A時,顯然有a=3。

當B={1},{2},或者?時,方程x2-a x+2=0有等根,或者無實根,故Δ≤0,即a2-8≤0。解得

故所求a值的集合為