先猜后證的數(shù)學(xué)思想及其應(yīng)用

朱懷靜

摘 要：先猜后證數(shù)學(xué)思想是數(shù)學(xué)思想的重要組成部分，它將猜想與證明相結(jié)合，是一種創(chuàng)新。沒有先猜后證，許多定理的證明將十分困難。文章先介紹了先猜后證數(shù)學(xué)思想的概念以及重要性，而后說明了先猜后證數(shù)學(xué)思想的在定理、引理證明以及解題時的應(yīng)用，有助于高校學(xué)生在數(shù)學(xué)學(xué)習(xí)的過程中注重先猜后證思想的學(xué)習(xí)與理解，從而促進(jìn)其對數(shù)學(xué)的學(xué)習(xí)。

關(guān)鍵詞：先猜后證 數(shù)學(xué) 合情推理

引言

數(shù)學(xué)思想是千百年來人們對數(shù)學(xué)事實(shí)與理論經(jīng)過概括總結(jié)后得出的對數(shù)學(xué)本質(zhì)的認(rèn)識。只有通過數(shù)學(xué)思想的培養(yǎng)，人們的數(shù)學(xué)能力才能有大幅度的提高。有人曾說過，掌握了數(shù)學(xué)思想，就是掌握了數(shù)學(xué)的精髓。先猜后證是數(shù)學(xué)思想里的重要組成部分。許多定理、引理的證明都離不開這一思想。因此，了解與掌握先猜后證這一數(shù)學(xué)思想不僅有助于中小學(xué)生掌握數(shù)學(xué)知識，對高校學(xué)生數(shù)學(xué)的學(xué)習(xí)也有極大的幫助。^[1]

一、先猜后證數(shù)學(xué)思想的介紹

先猜后證數(shù)學(xué)思想是一種重要的數(shù)學(xué)思想，這里筆者主要介紹其概念及在數(shù)學(xué)發(fā)展歷程中的重要作用。

1.先猜后證的概念

在數(shù)學(xué)領(lǐng)域中先猜后證是一種重要的數(shù)學(xué)思想，既能夠進(jìn)行猜想運(yùn)動，又能夠?qū)Σ拍軇?chuàng)新進(jìn)行證明，從一定程度上來說先猜后證思想對于數(shù)學(xué)學(xué)習(xí)過程中常規(guī)打破、標(biāo)新立異，并對傳統(tǒng)習(xí)慣性思維進(jìn)行超越具有一定的促進(jìn)作用，是一種能夠通過現(xiàn)象看本質(zhì)的更高層次的思維。創(chuàng)造性的思之所以稱之為是創(chuàng)造性思維必須有創(chuàng)造性的想象，愛因斯坦曾說過：想象力是科學(xué)研究中的一個實(shí)在因素。相較于知識來說想象力其實(shí)更為重要，想象力是無限的，而知識是有限的，通過想象力能夠?qū)κ澜缟系囊磺惺挛镞M(jìn)行概括，推動知識的發(fā)展進(jìn)步。想象力對于知識來說其進(jìn)化的源泉。^[2]

2.先猜后證的重要性

在整個人類數(shù)學(xué)史發(fā)展過程中，我們可以發(fā)現(xiàn)其中很多歷史性突破和重要的發(fā)現(xiàn)中都有先猜后證的身影在其中發(fā)揮作用，在一個理論證明之前首先需要通過猜想發(fā)現(xiàn)一個命題的內(nèi)容之后，還需要不斷地對其進(jìn)行檢驗(yàn)以及修改，幫助猜想和理論能夠不斷地完善最終實(shí)現(xiàn)完全證明，實(shí)現(xiàn)對證明進(jìn)行推測。在對觀察到的結(jié)果加以綜合類比的一整個系列過程中先猜后證都起到非常重要的作用，從發(fā)現(xiàn)——猜想這就是整個先猜后證數(shù)學(xué)思想的實(shí)質(zhì)所在，而牛頓曾說過，沒有大膽的猜想，就做不出偉大的發(fā)現(xiàn)。從種種角度足以看出整個數(shù)學(xué)發(fā)展過程中先猜后證所起到的重要作用。

在數(shù)學(xué)的發(fā)展過程中其中絕大多數(shù)數(shù)學(xué)方法、法則、定理規(guī)律等發(fā)現(xiàn)和發(fā)展過程中先猜后證都是其中一個非常重要的方法，并且在對各種數(shù)學(xué)問題發(fā)現(xiàn)并解決的過程中不能夠僅僅的按照邏輯程序?qū)栴}進(jìn)行思考，還需要將自己的經(jīng)驗(yàn)和邏輯推理方法兩者之間進(jìn)行結(jié)合，從而將跳躍式思維更多地表現(xiàn)出來。在高校數(shù)學(xué)教學(xué)的過程中，老師們不僅僅需要對思維的嚴(yán)密性以及結(jié)果的正確性進(jìn)行強(qiáng)調(diào)，同時也需要提高對思維的直覺探索性以及發(fā)現(xiàn)性進(jìn)行提升，這對于學(xué)生創(chuàng)新以及綜合能力的提升和培養(yǎng)有非常重要的作用。總的來說要加強(qiáng)對學(xué)生先猜后證思維的培養(yǎng)和重視，可以從一定程度上對學(xué)生的數(shù)學(xué)素質(zhì)以及開放型的思維這些提升。首先在問題解決的基礎(chǔ)上，更多的將學(xué)生已有的數(shù)學(xué)活動經(jīng)驗(yàn)作為其基礎(chǔ)之后，再通過先猜后證的方式對整個問題的條件進(jìn)行分析，將已知的條件和位置的結(jié)構(gòu)之間通過先猜后證的方式進(jìn)行聯(lián)系，進(jìn)一步地對問題解決的效率進(jìn)行提升。

二、先猜后證數(shù)學(xué)思想的應(yīng)用

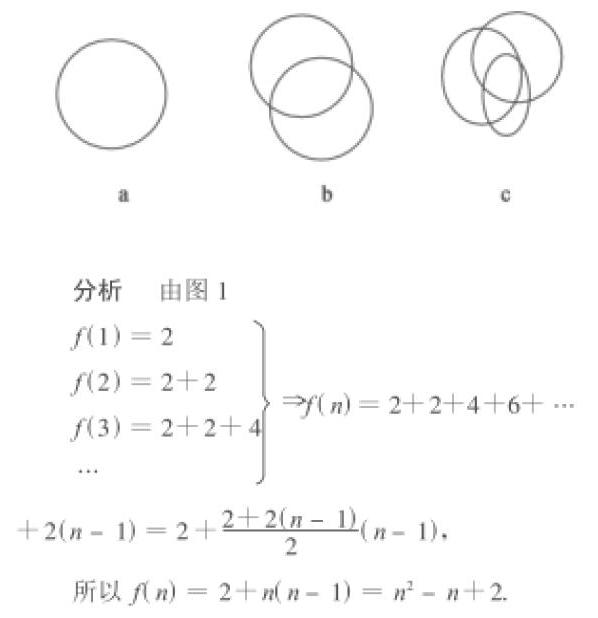
比如說在進(jìn)行虛數(shù)的教學(xué)過程中。可以讓學(xué)生們對自然系數(shù)逐步擴(kuò)充到實(shí)數(shù)系的整個過程進(jìn)行回顧，并從中體會到在整個數(shù)系擴(kuò)充所存在的緊密聯(lián)系。在敘述運(yùn)算進(jìn)行學(xué)習(xí)過程中，可以通過類比實(shí)數(shù)運(yùn)算的法則對其需進(jìn)行探究，在得出運(yùn)算結(jié)果的同時還可以對運(yùn)算過程中所蘊(yùn)含道理進(jìn)行充分了解。比如說是在對虛數(shù)加法法則進(jìn)行學(xué)習(xí)的過程可以通過不完全歸納的方法、類比物理中力的分解及相加或者是向量加法的方法對學(xué)生有實(shí)際經(jīng)驗(yàn)的方向問題進(jìn)行推理得出，對于同一個問題可以從多角度進(jìn)行分析并得出相應(yīng)的結(jié)論。不完全歸納推理的方式和形式不僅僅能夠?qū)μ摂?shù)的加法法則進(jìn)行學(xué)習(xí)過程中可以使用，還能夠在虛數(shù)的加乘法各運(yùn)算律的計(jì)算和推理過程中進(jìn)行使用。例如：平面內(nèi)的 n 個圓 ，最多可將平面分割多少個互不重疊部分區(qū)域這個實(shí)際問題可轉(zhuǎn)化為數(shù)學(xué)問題 ：f（1） =2 ;f（2） =2 +2 ;f（3） =2 +2 +4 ;f（n） =2 +2 +4 +6 +… +2（n - 1），求 f（n）的表達(dá)式，其所闡述的實(shí)際問題是有n個圓，其中任意兩個圓都相交于兩個不同的點(diǎn)，并且第三個園都不會在此點(diǎn)相交，問這n個圓將平面分成多少個不連通的部分，并加以論證。

結(jié)語

綜上所述，作者在本文之中對其進(jìn)行了深入的探究，希望能夠給予大家一些啟發(fā)。布魯納曾靜說過探索是數(shù)學(xué)教學(xué)的生命線。意味著探索真理的方法是在數(shù)學(xué)教學(xué)之中非常關(guān)鍵的一步，其中歸納猜想和類比猜想都是其中相對比較重要的兩個板塊。在本文之中首先以先猜后想為基礎(chǔ)，對于學(xué)生在學(xué)習(xí)過程之中要先學(xué)會這樣的方法，其余在教會學(xué)生要獨(dú)立自主的主動學(xué)習(xí)的方式進(jìn)行學(xué)習(xí)。希望高校學(xué)生能夠在文章的基礎(chǔ)上更深入地了解先猜后證這一數(shù)學(xué)思想，在今后的數(shù)學(xué)學(xué)習(xí)中積極運(yùn)用這一思想解決問題。

參考文獻(xiàn)

[1]余德治.先猜后證的數(shù)學(xué)思想及其應(yīng)用[J].中學(xué)數(shù)學(xué)雜志，2016（6）：19-22.

[2]黃坪.先猜后證，讓思維活起來[J].數(shù)學(xué)教學(xué)，2014（5）：7-8.