基于QR-GED-EGARCH模型的上證180指數(shù)風險度量分析

卞 蕾 王慧龍 胡夢婕

（安徽大學 ，安徽 合肥 230601）

一、引言

近年來，隨著金融創(chuàng)新的深化和經(jīng)濟金融全球化趨勢的加強，使金融市場更加動蕩，金融機構面臨的風險加大。“2017中國金融風險管理高峰論壇”提出要將金融風險管理從日常管理提升為戰(zhàn)略管理，逐漸成為整個金融體系運行和管理的核心。VaR方法，作為一種金融風險管理工具，它利用統(tǒng)計思想對風險進行估值，該方法在風險測量、監(jiān)督等領域被廣泛應用，成為市場風險測量的主流方法。

VaR是金融頭寸在給定一個時間段內(nèi)一定置信水平下的最大損失。對VaR值的計算實質(zhì)上就是研究序列的波動率，針對收益率序列呈現(xiàn)的尖峰厚尾、波動集聚性及不對稱性特征，利用GARCH族模型來擬合。國內(nèi)外許多學者做了很多關于金融時間序列風險度量的研究，ARCH模型最開始由Engle[1]提出，隨后Bollerslev[2]在此基礎上，將過去的條件方差引入條件方差模型得到了GARCH模型；由于杠桿效應的存在，Nelson[3]提出了EGARCH模型，該模型能準確地描述金融序列呈現(xiàn)的非對稱性特征。GARCH模型族都是假定收益率序列服從某一分布下進行VaR度量，研究表明，基于正態(tài)分布下VaR參數(shù)法在一定置信水平下計量VaR時會嚴重低估風險，在對正態(tài)分布提出質(zhì)疑后，研究人員進行了大量的探索，陸續(xù)提出偏 t分布[4]、廣義誤差分布[5]、Pareto 分布[6]、穩(wěn)定分布[7]、g-h分布[8]等，并將其應用到風險度量中。以上研究在一定程度上解釋了收益率序列存在的尖峰厚尾以及波性集聚特征，卻不能全面度量收益率序列的風險。Engle和Manganelli[9]提出了基于分位數(shù)理論進行度量VaR的CAViaR模型,無須對尾部分布等進行假設，直接對VaR本身進行建模。Chen和Kang[10]將CAViaR模型用于對股市風險度量研究中，陳耀輝和朱盼盼[11]將其應用到匯率風險研究中,將GARCH模型與分位數(shù)回歸模型相結合進行比較分析。劉亭和趙月旭[12]利用QR-t-GARCH模型對滬深指數(shù)收益率進行了風險度量研究，結果發(fā)現(xiàn)加入分位數(shù)回歸的GARCH（1，1）模型較 GARCH（1，1）對收益率風險度量效果更好。簡志宏等采用了CAViaR-EVT模型對極端隔夜風險進行預測，實證結果表明其預測效果比EVT和GARCH-EVT模型更合理[13]。曾裕峰和張涵[14]分別采用CAViaR模型和GARCH模型對VaR進行風險建模，結果發(fā)現(xiàn)CAViaR模型在股指期貨風險預測方面具有明顯優(yōu)勢。分位數(shù)回歸理論應用于VaR計算可以比較全面地度量收益率序列的風險，也無需假定服從任何分布，是一種半?yún)?shù)估計方法。有關GARCH族模型和分位數(shù)回歸模型相結合的研究較少，大量研究還是集中在兩種方法的孤立應用上。

而針對存在杠桿效應所提出的EGARCH模型，它在與分位數(shù)回歸結合后，其度量風險的精確度是否高于EGARCH模型？本文利用GARCH模型和EGARCH模型并將分位數(shù)回歸結合構造的QRGARCH、QR-EGARCH模型，在考慮上證180指數(shù)收益率序列服從正態(tài)分布、t分布、偏t分布、GED分布、偏GED分布的情況下，選取1%和5%兩個不同的置信水平，以求找到最優(yōu)的擬合模型。

二、模型與VaR方法

（一）GED-EGARCH 模型

GARCH模型在處理金融時間序列時存在一些弱點，如要求無條件方差必須非負以及它對正負擾動的反應是對稱的。為了克服這些弱點，Nelson提出了EGARCH模型，該模型既放松了對GARCH模型參數(shù)的非負性約束，又反映了杠桿效應，GED分布是一種更為靈活的分布形式，通過對其參數(shù)的調(diào)整，GED分布的尾部厚薄也會有所變化，能更好地處理收益率的厚尾現(xiàn)象。

（二）QR-GED-EGARCH（1,1）模型

分位數(shù)回歸 （QR）描述的是當給定回歸變量X時，響應變量Y在不同分位數(shù)下的變化趨勢，該思想最早是由Koenker和Bassett[15]提出來的，它是將響應變量看作是其他變量的線性函數(shù)，從而推導出回歸系數(shù)的漸近分布，Taylor[16]將分位數(shù)回歸應用到VaR的計算上，其表達式為：

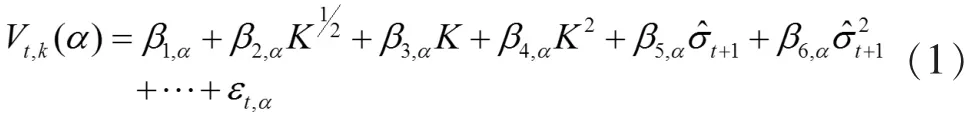
Chen[17]利用上述思想，對日經(jīng)225股票指數(shù)進行具體分析，利用分位數(shù)回歸方法，將收益率作為響應變量，K和作為回歸變量對收益率序列進行相關風險度量。

借鑒上述研究，本文采用模型如下：

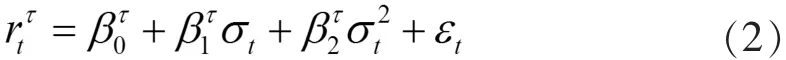
其中，σt的估計值的值由GED-EGARCH（1,1）模型得到，βτ的估計值由分位數(shù)回歸法通過求解以下公式得到：

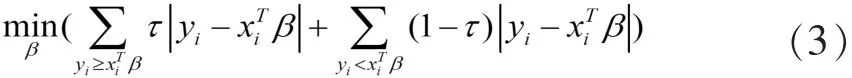
（三）VaR的計算原理

VaR又稱風險價值，它可以定義為金融頭寸在給定一個時間段內(nèi)一定的置信水平下發(fā)生的最大損失。即，假設 F（x）為的積累分布函數(shù)，且該金融頭寸的收益率分布下側分位數(shù)為，那么VaR在置信水平1-下的計算公式為：

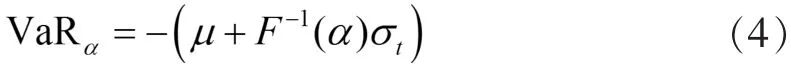
三、上證180指數(shù)收益率的實證分析

（一）數(shù)據(jù)選取與處理

本文選取上證180指數(shù)日收盤價作為研究對象，時間區(qū)間為2010年6月1日到2018年4月27日，本文把股票日收益率定義為

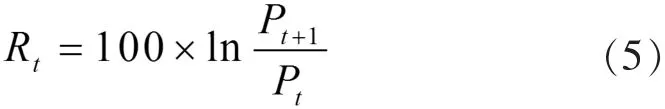
其中Pt表示股票指數(shù)日收盤價格，Rt表示日股票指數(shù)收益率序列，數(shù)據(jù)來源于同花順軟件，研究采用的軟件有Eveiws9和R語言。

（二）上證180指數(shù)日對數(shù)收益率特征的檢驗

1.正態(tài)性檢驗

上證180指數(shù)日對數(shù)收益率的基本統(tǒng)計特征分析如表1所示：

表1 收益率的描述性統(tǒng)計量

由表1可知，上證180指數(shù)對數(shù)收益率序列偏度為-0.721,23，小于0，說明序列分布有長的左拖尾。峰度為8.813,84，遠高于正態(tài)分布的峰度值3，說明收益率序列具有尖峰和厚尾的特征。Jarque－Bera統(tǒng)計量為2,872.005，值近似為零，拒絕該對數(shù)收益率序列服從正態(tài)分布的假設。為了更直觀地看出序列的尖峰厚尾和不服從正態(tài)分布的特征。下面做出上證180指數(shù)日對數(shù)收益率的Q-Q圖和分布擬合圖。

圖1顯示，QQ圖偏離直線的程度較高，可以認為樣本數(shù)據(jù)不服從正態(tài)分布。且從圖2可以看出，收益率分布對比正態(tài)分布具有很明顯的尖峰厚尾特征，故不能用正態(tài)分布來擬合數(shù)據(jù)分布，而需要用其他的分布去估計GARCH模型的參數(shù)。

2.序列自相關性檢驗與平穩(wěn)性檢驗

對收益率的自相關性進行分析，發(fā)現(xiàn)大部分樣本自相關系數(shù)和偏自相關系數(shù)都在零值附近波動，且由Q統(tǒng)計量及其伴隨概率可知，在5%的顯著性水平下，接受原假設，即收益率序列不具有自相關性。接下來，對該序列進行ADF單位根檢驗，檢驗結果如表2所示：

圖1 上證180指數(shù)正態(tài)Q-Q圖

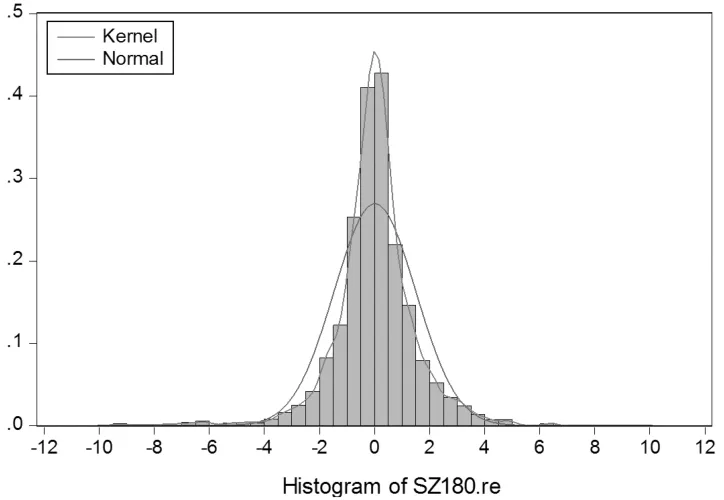
圖2 上證180指數(shù)收益率分布擬合圖

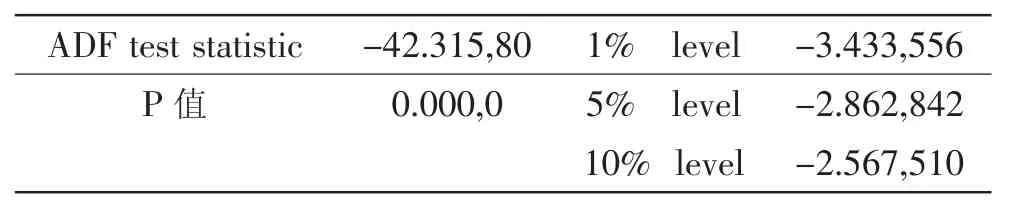
表2 數(shù)據(jù)的單位根檢驗結果

其中，t統(tǒng)計量的值為-42.315,80，對應P值接近0，表明序列平穩(wěn)。在1%、5%、10%的顯著性水平下，上證180收益率序列均拒絕隨機游走的假設，說明該序列是平穩(wěn)的。

3.ARCH效應檢驗

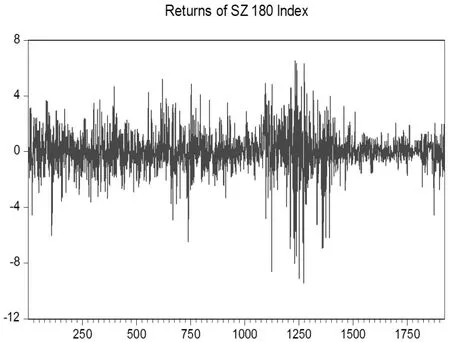
圖3 上證180日對數(shù)收益率

由圖3可以看出股指收益序列呈現(xiàn)出一種波動的聚集性，從直觀上看序列可能存在異方差性以及杠桿效應。對序列進行LM檢驗異方差性，結果如下表3所示：

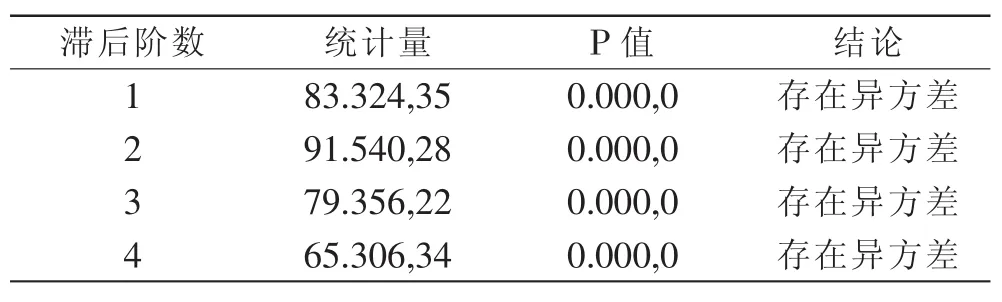
表3 LM異方差檢驗

（三）模型的建立與估計

1.GED-GARCH（1,1）模型估計及計算

由上述分析可知，收益率序列具有分布的尖峰厚尾性，波動的集聚性以及信息不對稱性特征。因此建立GED-GARCH模型對收益率序列進行估計，滯后階數(shù)（p,q）選擇（1,1）。 將其與基于正態(tài)分布、t分布、偏t分布、GED分布和偏GED分布的GARCH、EGARCH模型相比較，通過比較 AIC、SC值，選出最優(yōu)模型，其檢驗結果如下表所示：

由信息最小化準則可知，建立收益率序列服從GED分布的EGARCH模型效果最佳，估計參數(shù)的結果如表4所示：

由表5結果可知，除參數(shù)均值μ以及非對稱系數(shù)γ不顯著外，其余參數(shù)均顯著，具體構建的 GEDGARCH（1,1）模型結構如下所示：

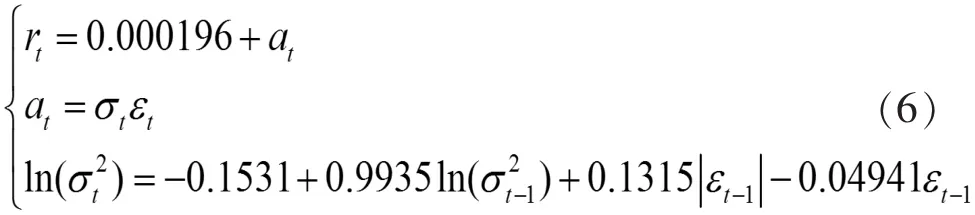
由此模型可以看出：α+β>1，說明收益率的波動具有持久性，當前信息對預測未來的條件方差有重要意義；γ<0，說明了相同單位的利壞信息沖擊對波動的影響要比利好信息沖擊來的大。接下來，對得到的模型進行檢驗，標準化后的殘差過程的統(tǒng)計量為 Q（10）=17.670（0.061）和 Q（20）=24.348（0.228），而平方過程，其對應的統(tǒng)計量為Q（10）=14.199（0.164）和 Q（20）=21.083（0.392），括號中的參數(shù)是其對應的P值。因此，在擬合的標準殘差序列中不存在相關性，說明所擬合的模型是合適的。

綜合以上分析，基于GED分布的EGARCH模型對比其他分布下的模型能更好的擬合收益率的波動。

下面，利用VaR的計算公式，在給定分位點為0.05和0.95的情形下，計算出了GED-EGARCH（1,1）模型的值，并作出動態(tài)走勢圖（如圖4）。

2.QR-GED-GARCH（1,1）模型的建立

在上文所得到的GED-GARCH （1,1）模型基礎上，現(xiàn)將分位數(shù)回歸方法應用到該模型中，由2.2節(jié)方法可知，模型的結構為：

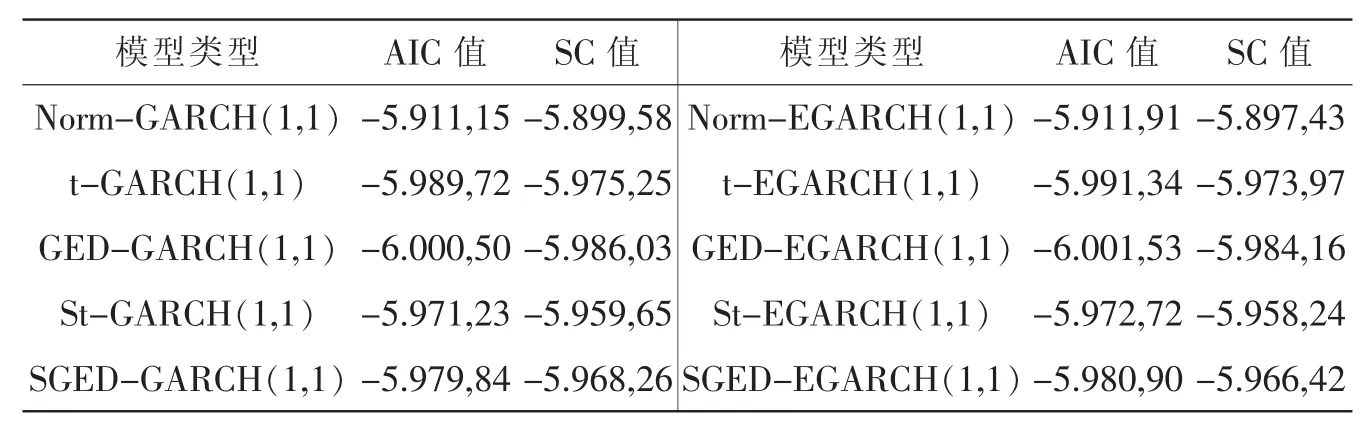
表4 AIC、SC值比較

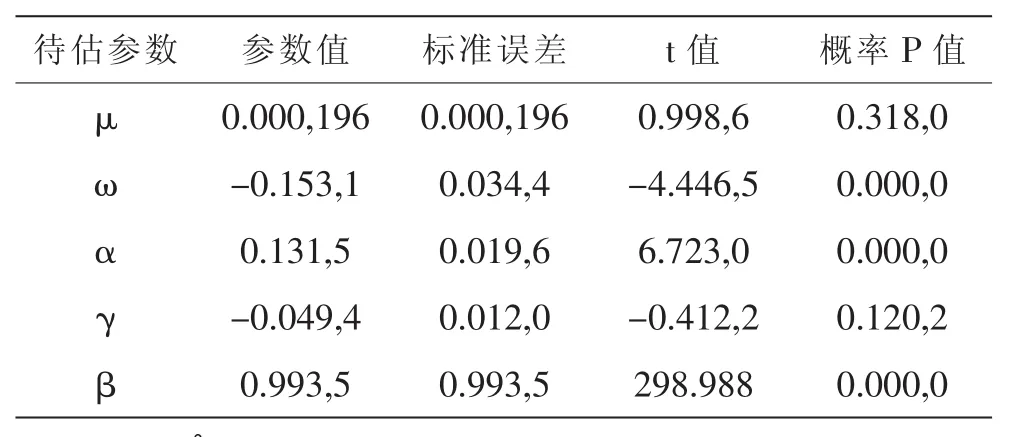
表5 基于GED分布的EGARCH模型估計參數(shù)表

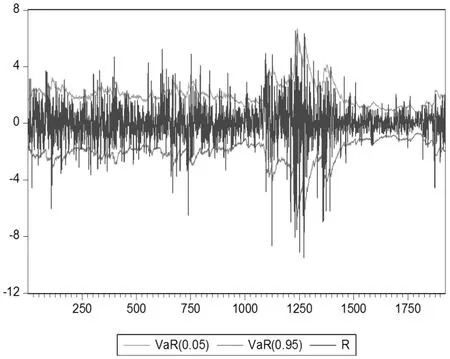
圖4 GED-GARCH（1,1）模型動態(tài)走勢

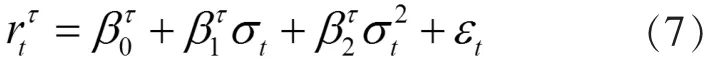
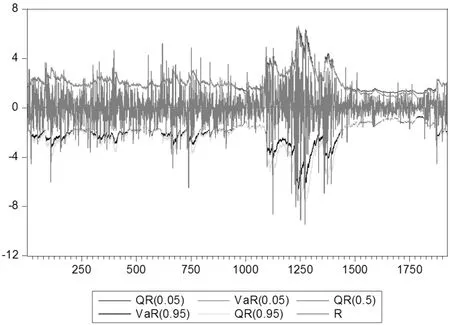
圖5 兩類模型動態(tài)走勢比較圖

由圖5可以很明顯看出，分位數(shù)取0.5時，VaR值的波動變化很不明顯，其趨勢圖趨近于一條直線，在分位點為0.05，0.95時，其波動效果明顯，且與實際收益率的波動值趨勢一致，這也說明了分位數(shù)回歸模型不僅能對股票收益率序列進行全面描述，而且對其尾部特征能進行更好的描述，也適應了金融時間序列高峰厚尾的特點。比較兩類模型的走勢可以發(fā)現(xiàn)，在分位點0.95時，兩類模型變化趨勢趨于一致，而在給定分位點為0.05，其對應95%置信水平下時，兩類模型的值波動的程度大小有較大差別，這說明對于極端情況下，對損失的敏感程度要高于收益，特別是在股票價格劇烈波動的時間區(qū)間里，加入分位數(shù)回歸后的模型避免了過于低估風險值，對風險有一個更為精確的刻畫。

（四）VaR的檢驗—Kupiec檢驗

通過模型進行預測后，需要對其預測值進行檢驗，來檢驗所構建模型的有效性。下面利用Kupiec[18]提出的似然比率檢驗法比較不同模型預測能力的可行性水平。假定考察天數(shù)為N，失敗天數(shù)為n，那么失敗頻率則為α*=N/n，我們所期望得到的預測結果為失敗頻率等于所給定VaR的置信水平α。模型估計太過保守，高估了風險。為此，Kupiec檢驗原理所建立假設如下，原假設和備擇假設分別是：

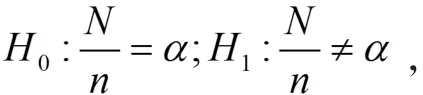
似然統(tǒng)計量為：

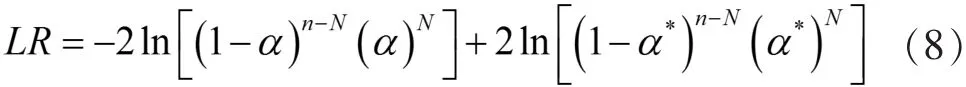
在原假設H0成立的條件下，似然統(tǒng)計量服從自由度為1的卡方分布。若出現(xiàn)失敗次數(shù)過多或者過少這樣的極端情況，則會拒絕原假設，模型失效。

由表6和表7失敗率檢驗結果，可以得出如下結論：

第一，針對GARCH族模型中同一模型的不同分布。在5%的顯著性水平下，基于t分布下模型的失敗天數(shù)少于基于GED分布下的模型，但其擬合成功率低于基于GED分布下的模型，說明在t分布下模型低估了風險。而在1%的顯著性水平下，基于t分布下模型的失敗天數(shù)要高于基于GED分布下的模型，其似然比率檢驗中P值均小于顯著性水平0.01，拒絕原假設，此時的t分布高估了風險，t分布無法在上證180指數(shù)風險度量中提供有價值的信息。且不管是在1%還是在5%情況下，GED分布均通過了檢驗，可見GED分布相比于t分布更能刻畫上證180指數(shù)收益序列的分布特征。

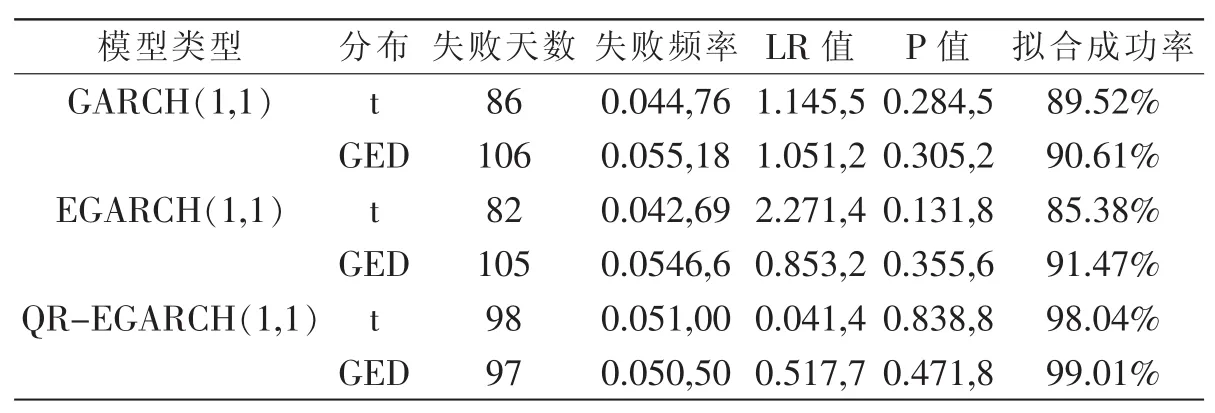
表6 5%顯著性水平下三種模型VaR失敗率檢驗

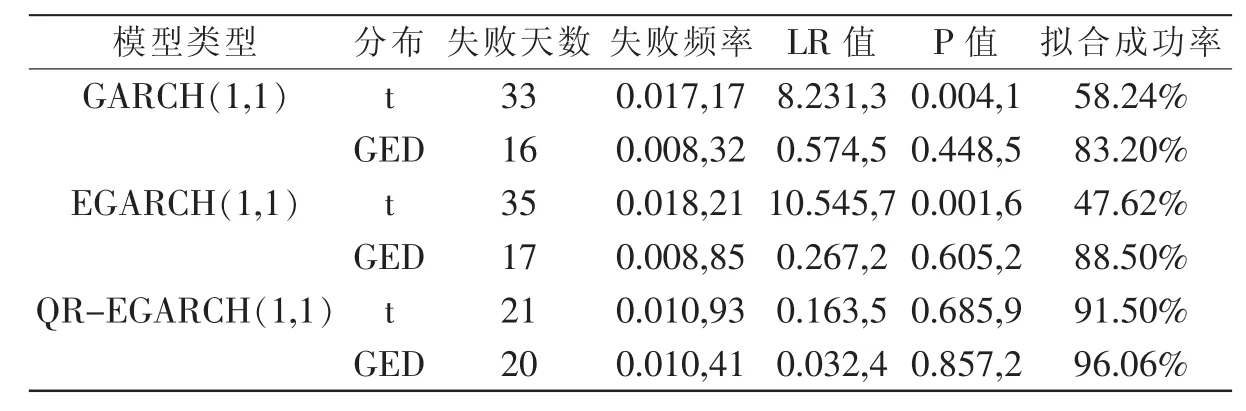
表7 1%顯著性水平下三種模型VaR失敗率檢驗

第二，對于GARCH族模型同一分布下不同模型，從似然比率LR統(tǒng)計量結果分析，基于t分布下的EGARCH模型并未表現(xiàn)出比傳統(tǒng)GARCH模型更優(yōu)越的風險測度能力。而在基于GED分布下EGARCH模型的擬合成功率高于傳統(tǒng)GARCH模型，這說明了t分布與傳統(tǒng)GARCH模型結合，GED分布與EGARCH模型結合應用于風險度量中更合適。在5%的顯著性水平下，GED-EGARCH（1,1）模型的預測精度要優(yōu)于其他三類模型，其擬合成功率達到了91.47%，說明了GED分布和EGARCH模型的結合能很好地描述上證180指數(shù)所存在的尖峰厚尾、波動集聚性以及杠桿效應。

第三，在上述基礎上，將分位數(shù)回歸引入到EGARCH模型中，其預測精度有了顯著地提高，且明顯高于前兩類模型。可以很明顯看出QR-GED-EGARCH（1,1）模型對上證180指數(shù)風險的預測效果較其他模型表現(xiàn)更為優(yōu)異。

綜上所述，由于分位數(shù)回歸模型無須事先設定誤差分布函數(shù)的特定形式，并能全面地度量風險，其與GED-GARCH （1,1）模型結合后所構造的QRGED-EGARCH（1,1）模型，對上證180指數(shù)收益序列的風險有更為精確地測度。

四、結論與思考

本文在運用分位數(shù)回歸方法以及考慮收益率序列具有杠桿效應的的情況下構建了QR-GED-EGARCH模型，對上證180指數(shù)收益率序列風險值進行了動態(tài)建模分析，并與基于t分布和GED分布下的GARCH和EGARCH、以及QR-t-EGARCH進行比較，利用Kupiec檢驗來比較各個模型擬合收益率序列的準確程度。研究結果表明，從序列波動性特征來考慮，應用EGARCH模型對風險值進行測算，較好的反映了上證180指數(shù)收益率序列所具有的“杠桿效應”，且收益率序列拒絕服從正態(tài)分布的假設，故利用了能描述序列尖峰厚尾特征的t分布和GED分布，Kupiec檢驗結果表明基于GED分布下的模型其預測精度普遍高于t分布下的模型，在此基礎上，引入分位數(shù)回歸后所構建的QR-GED-EGARCH模型擬合成功率為99.01%，優(yōu)于其他模型，說明其QR-GED-EGARCH全面地描述收益率序列特征，并且對風險值有一個精確的刻畫。