數形結合思想在高中物理解題中的應用
張郡麟
摘 要:物理作為一門抽象性較強的學科,需加強對數形結合思想的有效應用。本文首先分析了數形結合思想的含義,然后探討了其在高中物理解題中的具體應用,以供相關教學工作者參考。
關鍵詞:數形結合思想; 高中物理; 物理解題
中圖分類號:G633.7? ? ? ? ? ? ? 文獻標識碼:A? ?文章編號:1006-3315(2019)05-013-001
1.數形結合思想概述
數形結合思想主要是有效聯系數與形之間的關系,在綜合分析題中圖形的基礎上,對其中的數學表達式進行明確,從而解決物理問題。將數形結合思想應用于高中物理的解題過程中,可以進一步了解題目中包含的數量關系,從而創建合理的數學方程式,簡化題目的復雜效果,提升解題速度。在物理教學中充分發揮數形結合方式的作用,可以作為一種有力的工具和方法,來解決需要解答的物理難題。物理學科中包含著大量的數學關系和物理思想,因此,為了保證一個較好的物理教學效果,可以深入滲透數形結合思想。
2.在高中物理解題過程中,數形結合思想的具體應用
2.1以數解形
為了更加方便的描述物理問題,大都采用圖像來表示出與問題相關的信息。圖像既具有一定的優勢,如形象、直觀,同時還存在著一定的缺陷,如準確性不高。在解決物理問題時,需加強對圖像的分析和理解,充分挖掘出其中的有用信息,并且對圖形與物理量之間的關系進行明確,通過分析其中的物理規律,來合理轉換圖像問題,從而實現對物理問題的有效解決。
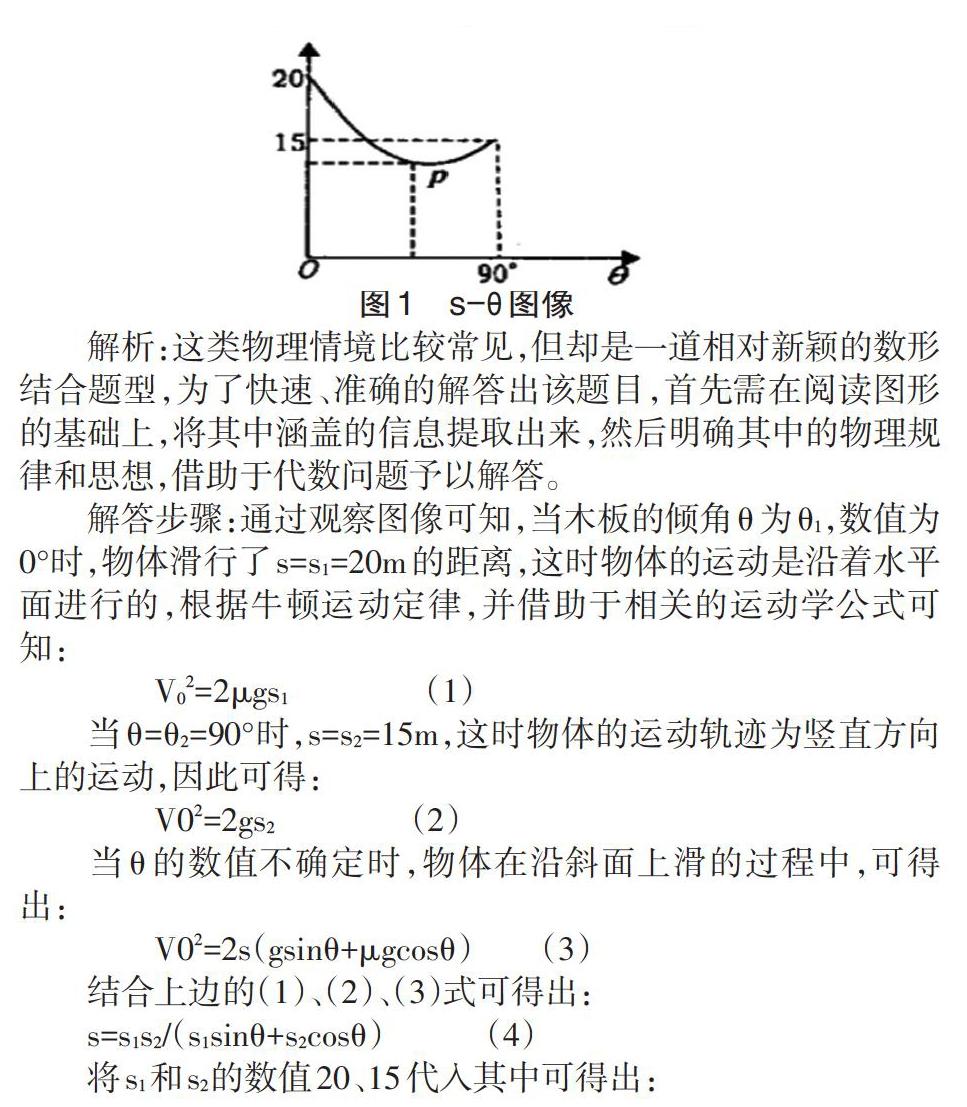
例1,物體在沿著傾斜的木板進行滑動時,初速度為v0,并且數值的大小保持不變,根據木板傾角θ的變化,物體在上滑時,其滑動的距離s也在發生改變,如圖1所示,是在大量實驗的基礎上,所得到的距離s與傾角θ的s-θ圖像,求解出圖形的最低點p的位置坐標。
解析:這類物理情境比較常見,但卻是一道相對新穎的數形結合題型,為了快速、準確的解答出該題目,首先需在閱讀圖形的基礎上,將其中涵蓋的信息提取出來,然后明確其中的物理規律和思想,借助于代數問題予以解答。
解答步驟:通過觀察圖像可知,當木板的傾角θ為θ1,數值為0°時,物體滑行了s=s1=20m的距離,這時物體的運動是沿著水平面進行的,根據牛頓運動定律,并借助于相關的運動學公式可知:
因此,為了得到距離s的最小值,θ的數值需為53°,這時s=12m,因此,圖形的最低點位置p的坐標為(53°,12m)
2.2以形助數
以形助數即是依據圖形來解決物理問題,通過仔細觀察和處理圖形,促使抽象的物理概念具體化,并且將其轉化為形象的圖形語言,從而簡化問題復雜程度。有些物理問題在解決時,針對其中的已知量和未知量,很難明確它們之間的關系,為此,大都需要借助一些運動草圖和受力分析圖來協助分析問題,并且創建相應的關系方程予以求解;在使用代數運算的方式,難以有效解答出有些問題時,可以對其進行轉化,借助圖形將其解決。在解釋與物理相關的概念、規律及現象時,可以使用數學語言、文字語言、物理語言進行解決。一般情況下,大都采用文字語言來闡述物理問題,為了解決問題,可將其轉化為物理語言,借助于一些草圖進行描述,從而簡化問題的難度,促使學生明白題目中的物理量關系,并借助于方程式進行解答。
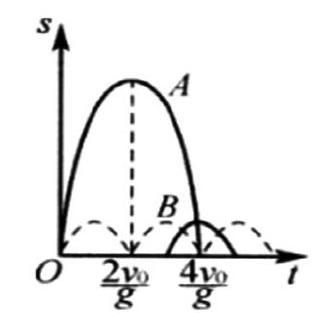
例2,以初速度2v0從地面上向上拋出A物體,方向為豎直方向,然后再以初速度v0在相隔Δt時間之后,豎直拋出物體B,為了確保二者可以在空中相遇,Δt的數值范圍是什么?
解析:將這兩個物體在豎直方向上的運動情況描繪在同一個坐標系中,如圖2的s-t圖像所示:
圖2物體A、B豎直運動s-t圖像
為了確保A與B相遇,需確保二者具有相同的拋出位移,即它們的圖形在坐標系中需具有相交點,根據圖示可知,物體B第一次與A相遇的臨界條件為物體B正好落到地面;物體B拋出的最遲狀態為物體B拋出的瞬間與A相遇。因此,為了確保A與B可以在空中相遇,Δt的數值范圍需為:
3.結語
綜上,在高中物理教學中,充分發揮數形結合思想的作用,具有非常重要的價值和意義,有助于簡化問題的復雜性,實現對抽象問題的有效解決。因此,數形結合思想的運用,可以讓學生快速了解解題的思路和方法,從而明確問題的解答方向,實現對物理問題的快速解答。為此,在實際應用過程中,教師需加強學生對這種解題方式的有效理解和掌握,強化他們對物理規律和概念的認識,從而為當前的物理教學工作提供有力指導和推動作用。
參考文獻:
[1]劉笑巖.數形結合思想在高中物理學習中的應用體會[J]考試周刊,2018(4):95-95

