Nesbitt不等式的精彩演繹

福建省仙游第一中學 (351200)

林碧霞

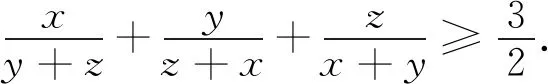
這個不等式形式優美，內涵極其豐富，由此可以演繹出一系列的不等式，可謂花團錦簇、精彩紛呈.

一、由Nesbitt不等式直接演繹

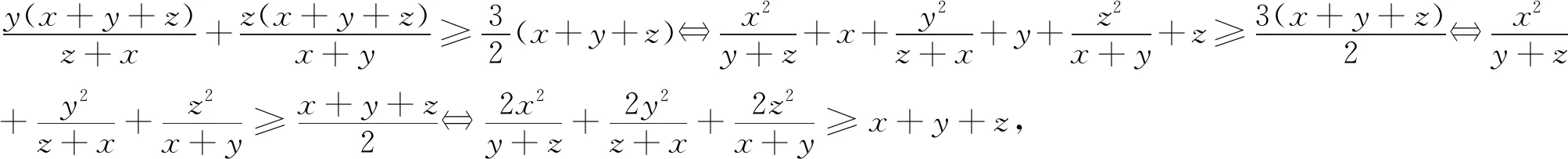
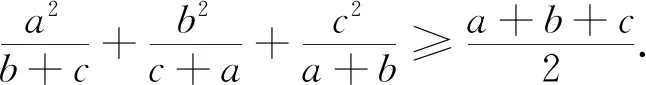
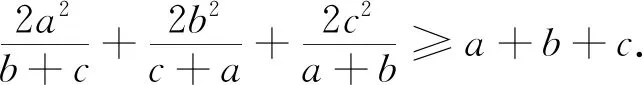
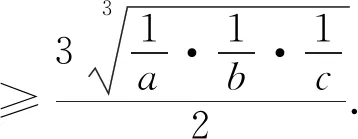
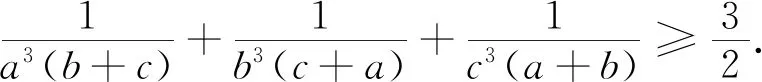
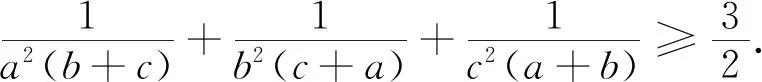
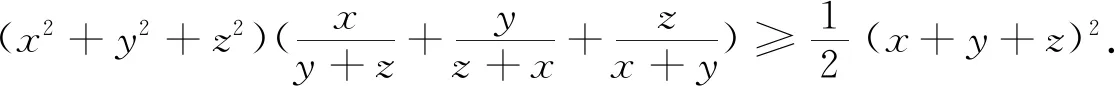
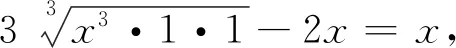
這就得到并證明了2006年白俄羅斯數學競賽試題.

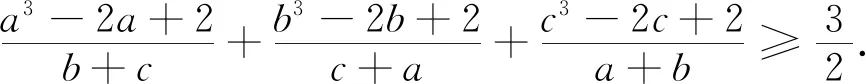
二、演繹Nesbitt不等式的變式

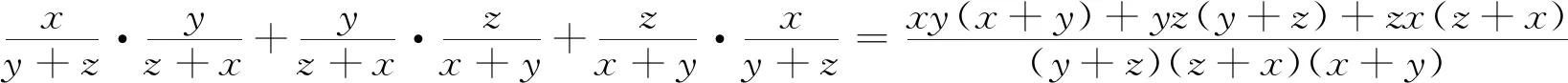
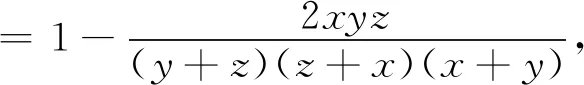
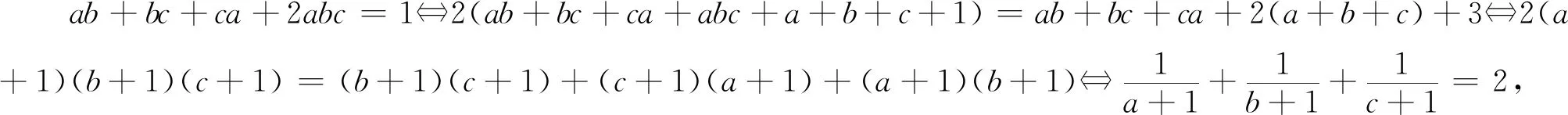
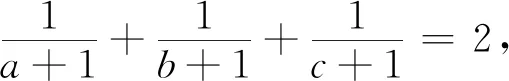
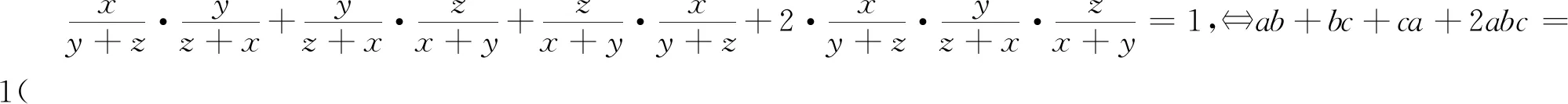
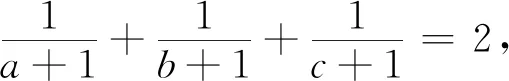
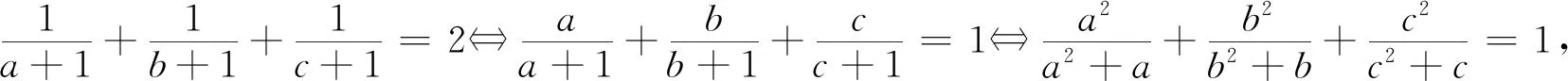
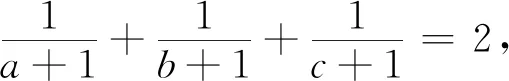
三、由Nesbitt不等式的變式再演繹

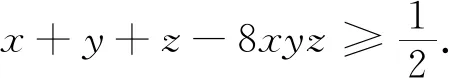
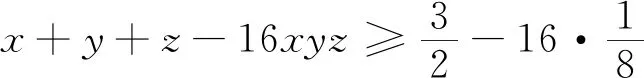
例8 已知x,y,z是正數，且xy+yz+zx+2xyz=1，證明：2(x+y+z)+1≥32xyz.

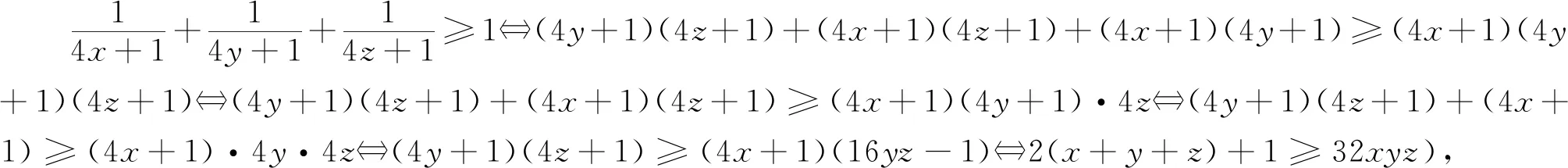
例10 已知x,y,z>0，且xyz+xy+yz+zx=4,求證：x+y+z≥3.

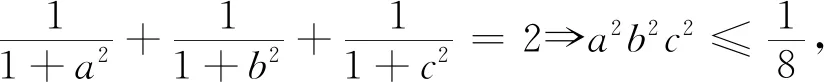
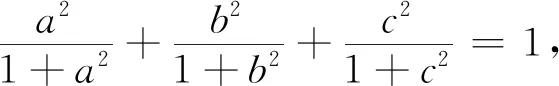
例13 設x,y,z>0,且xy+yz+zx+xyz=4，求證x+y+z≥xy+yz+zx.

例14 已知a,b,c>0,且abc=a+b+c+2,求證：ab+bc+ca≥2(a+b+c).