數(shù)形結(jié)合在初中數(shù)學教學中的應用

江蘇省昆山市石牌中學 王維娟

數(shù)學不僅需要研究數(shù)量關系，還要研究圖形，二者存在著對立和統(tǒng)一的關系，宇宙萬物無不是數(shù)和形的矛盾統(tǒng)一。對此，國內(nèi)外有很多專家對于數(shù)形結(jié)合都有著深刻的見解。我國著名數(shù)學家華羅庚說過：“數(shù)缺形時少直觀，形少數(shù)時難入微，數(shù)形結(jié)合百般好，隔裂分家萬事休。”數(shù)學中的很多概念、法則、公式、定理都與一定的空間形式密切聯(lián)系。數(shù)形結(jié)合是具體和抽象的結(jié)合，是形象思維和抽象思維轉(zhuǎn)化的橋梁，是邏輯含義和空間表達形式的展現(xiàn)。在拉格朗日的《數(shù)學概要》中描述：“只要代數(shù)同幾何分道揚鑣，它們的進展就是緩慢的，應用就狹窄，但當這兩門學科結(jié)成伴侶后，它們就互相汲取新鮮的活力，從此便以快速的步伐走向完善。”

初中階段正是學生打基礎的階段，教師應該重視數(shù)形結(jié)合的思想，通過多種方法不斷滲透到教學中。基于此，本文立足于初中數(shù)學教學，結(jié)合本人教學時的體會，對數(shù)形結(jié)合方法和思想進行相關的探討。

我們所接觸到的初中數(shù)學中，數(shù)形結(jié)合在不等式、數(shù)列、最值問題、函數(shù)和解析幾何等多方面都有涉及。

一、數(shù)形結(jié)合在不等式中的應用

例1：求不等式 |x+2|+|x-3| ＞5 的解集。

分析：這是一個絕對值不等式問題，既涉及了絕對值的知識點，還涉及了不等式里的知識點。

記數(shù)軸上表示數(shù)-2 的為點A，表示數(shù)3 的點為B，記表示數(shù)x的點為C，點C是數(shù)軸上的一個動點。“數(shù)軸”是初中數(shù)學中最基本的數(shù)形結(jié)合，也是初中數(shù)學中最早運用數(shù)形結(jié)合的一個例子。絕對值表示數(shù)軸上的一個點到原點的距離，而用兩數(shù)的差的絕對值表示數(shù)軸上兩點之間的距離。根據(jù)題意，畫出簡易數(shù)軸：

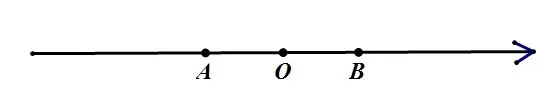
我們可以發(fā)現(xiàn)，點A和點B將數(shù)軸分成了三段，根據(jù)動點C的三個不同位置畫出三種不同情況下的數(shù)軸再一一進行分析。此時，這個問題就轉(zhuǎn)化為線段CA+CB＞5 的題目了。

通過觀察三張圖可以發(fā)現(xiàn)：當點C運動到點A和點B之間時，線段CA+CB=5；當點C運動到點A的左邊或者點B的右邊時，線段CA+CB＞5。

所以，我們就有結(jié)論：當-2 ≤x≤3 時，|x+2|+|x-3|=5；當x＜-2或x＞3 時，|x+2|+|x-3|＞5。

二、數(shù)形結(jié)合在二次函數(shù)中的應用

例2：已知點A（-1，y1）、B(-3，y2)、C(-2，y3)、D(1，y4)在函數(shù)y=x2+2x+2 的圖像上，比較y1、y2、y3、y4的大小。

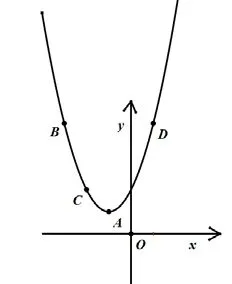
分析：我們已經(jīng)學過了二次函數(shù)的圖像，根據(jù)函數(shù)表達式畫出函數(shù)圖像，描出A、B、C、D這四個點的相應位置。那么，要比較y1、y2、y3、y4的大小就是看這四個位置的高低。如圖所示：

通過圖像，我們就可以馬上看出y1＜y2＜y3＜y4。用這樣的方法解決問題，就使得數(shù)學更形象、更直觀，數(shù)學就不那么枯燥了，數(shù)學也有美的一面，也讓那些后進的學生感覺到數(shù)學很有趣。

三、數(shù)形結(jié)合在數(shù)列計算中的應用

分析：我們可以這樣解：

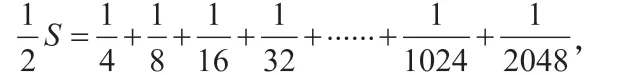
我們還可以試著通過圖形來理解。畫一個正方形，把這個正方形一分為二就得到，把其中一半再一分為二就得到，把的一半再一分為二就得到……畫完圖形之后我們可以發(fā)現(xiàn)：這些全部加起來就是用整個正方形減去右下角的最后一塊小正方形，也就是。如圖所示：

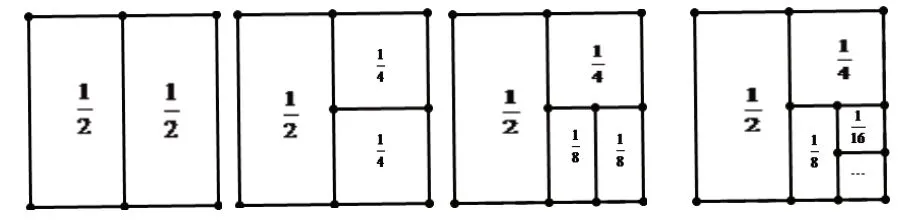
這樣的方法既簡單又直觀，容易理解，同學們一看就知道了，充分展現(xiàn)了數(shù)形結(jié)合的優(yōu)勢和奇特之處。

四、數(shù)形結(jié)合在勾股定理中的應用

分析：對于初中生來說，這種類型的題目是非常新穎的，以前沒有見到過。同樣，我們可以根據(jù)題意，構(gòu)造一個圖形，將題目轉(zhuǎn)化成圖形來解決。

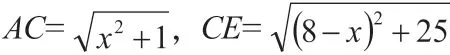
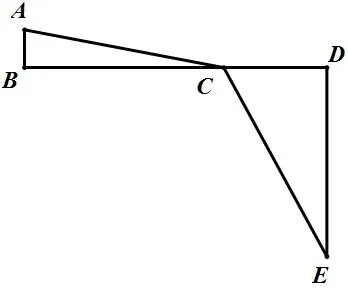
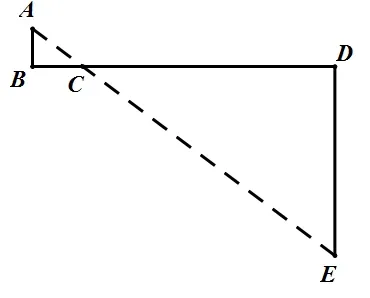
此時，上述問題就轉(zhuǎn)化成求AC+CE的最小值的問題了。到了這一步，同學們很容易想到：兩點之間線段最短。要求AC+CE的最小值，只需要連接AE，線段AE 與線段BD 的交點就是動點C 的位置。此時AE 的長度就是AC+CE 的最小值。如圖所示：

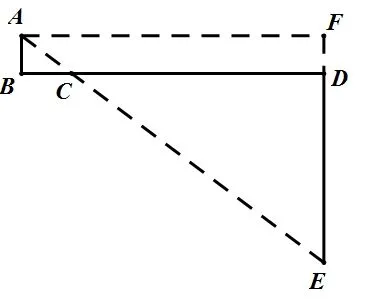
之后，過點A作AF平行且等于BD，連接BF，則在直角三角形AFB中，利用勾股定理即可求出線段AE的長度，也就是線段AC+CE的最小值。如圖所示：

如此，運用圖形將學生束手無策的最小值問題轉(zhuǎn)化成了熟悉的勾股定理的問題，不僅方便同學們理解，還降低了計算的難度，提高了做題的正確率。

在教學過程中，老師應鼓勵學生多利用圖形去研究、探索問題，培養(yǎng)學生的創(chuàng)造性思維和開放性思維，使同學們對數(shù)學學習更有興趣。

總之，作為一名初中數(shù)學教師，應該在傳授知識的同時，提高學生數(shù)形結(jié)合的能力，從“數(shù)”的方面、“形”的方面深化理解，形成直覺思維，從而順其自然地找到解題方法。在日常教學的過程中，教師要盡量利用多媒體教學，充分體現(xiàn)數(shù)字和圖形之間的聯(lián)系和變化規(guī)律，使學生理解更深刻，更靈活地掌握方法，充分觀察圖像，不管是靜態(tài)的還是動態(tài)的圖像，對它們的特點觀察得越仔細，思考得越深入，那么認識也就比較深刻，這樣遇到相關聯(lián)的情景時才能夠產(chǎn)生靈感，找到切入點解決問題。

當前，素質(zhì)教育已經(jīng)成為主流，對學生進行綜合素質(zhì)和能力的培養(yǎng)是建設創(chuàng)造性人才的需要。擁有創(chuàng)造性思維的人，才能更好地在各自的領域內(nèi)有所創(chuàng)新，推動科學技術和社會向前發(fā)展。教師應該發(fā)揮外因的作用，積極引導學生的興趣，發(fā)揮學生自主學習的內(nèi)在動因，學生才能長久受益。