基于JSD自適應粒子濾波的移動機器人定位算法

劉紅林，凌有鑄，陳孟元

(安徽工程大學 安徽省電氣傳動與控制重點實驗室，安徽 蕪湖 241000)

移動機器人定位就是確定機器人在其運動環境中的世界坐標系的坐標[1]，是機器人利用上一刻位姿和最新觀測信息來估計當前位姿的過程。移動機器人定位可以通過多種方法實現。蒙特卡羅[2]定位作為粒子濾波在移動機器人領域的成功應用,最早由Dellaertt[3]等提出。粒子濾波對后驗概率密度函數直接進行蒙特卡羅采樣使其逼近真實的概率分布,因而被廣泛應用在非線性系統。但是基于粒子濾波的MCL算法利用觀測似然評估每個粒子的重要性權重,在采樣環節中對先驗分布進行采樣,忽視了當前觀測信息,在預測過程中可能會出現粒子分布在似然函數的尾部的情況,從而引起粒子退化問題。目前，針對粒子退化問題主要有增加粒子數目、改進提議分布以及改進重采樣算法。第一種方法是擴大粒子數，但是比較低效，所以主要用選擇合適提議分布和對重采樣環節進行改進的方法來抑制粒子退化問題[4]。目前，提議分布的選取策略有將狀態轉移函數當作提議分布、把似然函數當作提議分布和混合提議分布等[5]。由于混合提議分布既考慮了狀態轉移函數，又考慮了似然函數，所以得到的重要性權值方差更小。雖然得到了較小的方差，但是在計算重要性權重時，難以實現計算過程中的積分運算。如果似然函數的分布呈峰態分布，那么采樣效率低下[6]。粒子濾波是用樣本來近似表示概率密度函數，用樣本均值取代積分過程，得到最小方差估計。如果粒子數較小，算法的誤差大，估計精度低，理論上如果粒子數目可以趨于無窮大，算法能夠得到最優估計，估計精度最高。可是粒子數量的大幅增加使得系統的計算量劇增，算法在實時性方面不能達標，其不足之處在此體現。Rao-Blackwellised[7]濾波方法的提出則從另外一個方向提高了算法的實時性。此方法通過HMM濾波、KF、PF算法三者結合，分開估計狀態向量中成員，使得估計維度減小，從而系統計算負擔得以減輕。Kwok[8]等提出RTPF算法，將粒子集通過擴展估計窗口進行劃分，使其成為一個個小粒子集，然后將小粒子集的估計結果通過賦予不同的權值重新組合獲得估計結果。研究者們將粒子集分割成相同大小的集合，以KL距離(Kullback-Leibler distance)為指標來獲取各集合的接近程度，從而動態調整粒子的數量提高實時性能。當算法性能較高時，采用較少的粒子數，否則采用較多的粒子數，這樣既滿足了濾波精度的要求，又減小了系統的計算負擔。由于KL距離沒有對稱特性[9]，所以當概率密度先后次序改變時，所得到的值也會改變，那么對集合間接近程度的衡量結果就會不準，采樣粒子數量的選擇也會受到影響，最終影響到估計結果。

研究在一般粒子濾波算法基礎上,通過對建議分布及重采樣過程加以改進，提出基于改進粒子濾波的移動機器人定位算法。該算法將先驗轉移概率密度和觀測似然概率密度的混合分布作為提議分布，將當前觀測信息融入進去，在混合分布基礎上，利用退火參數調控兩者在混合提議分布中的比例，對于退火參數取定值時的不足，通過優化機制對參數進行在線變更。同時，利用JS距離獲取子集間接近程度，確定采樣粒子的總數，動態改變粒子的數量。實驗結果顯示，改進算法在一定程度上解決了粒子退化以及多樣性缺失問題，減少了定位所需粒子數量，減輕了運算負擔，提升了算法精度。

1 移動機器人蒙特卡羅定位

定義移動機器人系統含有噪聲的運動學方程和觀測方程為：

(1)

式中,xk表示k時刻的運動狀態;f表示狀態轉移函數;uk表示k時刻的控制變量;ωk表示控制噪聲;zk表示系統在k時刻的觀測信息;g表示觀測函數;vk表示觀測過程中產生的噪聲。

定位的最終目的就是要獲得機器人在當前時刻的狀態xk。從貝葉斯濾波角度，問題求解的核心是估計后驗分布Bel(xk)。蒙特卡羅定位將具有不同權重的粒子重新整合，以此對k時刻機器人狀態的后驗概率進行估計。首先是重要性采樣[10]環節，從重要性概率密度q(xk|xk-1,zk,uk-1)采集加權粒子集合。再經過重采樣步驟，得到此刻狀態后驗Bel(xk)的離散估計。最后，為了解決積分難的問題，采用蒙特卡羅方法以采樣粒子平均值作為狀態估計結果。

(2)

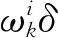
(3)

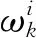
(4)

蒙特卡羅定位中建議分布的設計沒有融入當前觀測信息，把狀態轉移函數作為建議分布,即

q(xk|xk-1,zk,uk-1)=p(xk|xk-1,uk-1),

(5)

重采樣算法被用來克服樣本退化問題，在實際操作中，直接將評分過低的粒子舍棄，對評分高的粒子進行復制，重采樣之后保持粒子群數量基本不變。蒙特卡羅定位算法中重要性密度函數的設計，忽略了最新觀測zk對算法的影響，通過預測過程獲得的粒子集合會分布于似然函數的尾部,出現粒子退化現象，進而影響定位結果。

2 改進的蒙特卡羅定位算法

2.1 改進的粒子提議分布

針對粒子濾波中出現的粒子退化現象，采用設計更為合理的提議分布的方法來抑制粒子退化。學者們對先驗分布和后驗分布進行研究，分析兩種分布所具有的優點和缺點，在此基礎上混合提議分布思想出現了[11]。混合提議分布將兩種不同的分布放在一起進行研究。當前最新觀測信息的引入，使得混合提議分布比兩種單獨的提議分布具有較小的權重方差。可是，重要性權重的運算過程中出現了積分環節，難以完成。另外，在似然函數分布呈現出峰值分布的時候，采樣的效率極低[12]，所以使用退火參數來調整混合提議分布中各分布之間的比例。如果提議分布中的退火參數取值不變，因為概率分布具有不確定特性，所以濾波算法的性能較差。鑒于此，依據預測數據和觀測數據的關系來自動調整退火參數定位數值，實現自適應優化的目標。

在選擇建議分布q(xk|xk-1,zk,uk-1)時，將最新觀測zk融入到建議分布里，讓采樣環節得到的粒子集中地分布于高似然區域，能有效減輕粒子集合退化問題,提升濾波器性能。將先驗轉移概率密度和觀測似然概率密度的混合分布作為重要性密度函數，既考慮到運動模型又考慮到觀測模型，因此建議分布為：

q=p(zk|xk)p(xk|xk-1,ut-1)Bel(xk-1),

(6)

其相應的重要性權值計算式為：

ωk=ωk-1p(xk|xk-1,zk-1),

(7)

當使用退火參數對不同分布的混合率進行調整時，建議分布選擇為：

q=p(xk|xk-1,ut-1)cp(zk|xk)1-c,

(8)

則重要性權值計算式為：

(9)

其中，退火參數0≤C≤1。自適應調整退火參數的核心思想是在重要性采樣之后，對預測值和觀測值進行觀察比較，當觀測值比預測值大時，減小樣本重要性權重的占比，將C的數值往下降。反之，將C的數值往上升。

2.2 基于JSD的重采樣

重采樣過程的引入會產生粒子多樣性缺失問題，現采用遺傳學中的變異操作[13]對粒子集進行優化。將粒子分為高權重、低權重兩種，高權重粒子直接參與重采樣，低權重粒子經過變異操作后再參與重采樣。按式(10)確定低權重閾值，劃分出高權重粒子和低權重粒子。

(10)

(11)

式中，Lmax是群體中最大的適應度值；Lavg是每一代群體中平均的適應度值;L是要進行變異的個體的適應度值;Pm1和Pm2對應的是變異概率的最大值和最小值;β是常數。

粒子濾波使用采樣粒子與其權值的組合來表示系統后驗估計，其結果總存在誤差。理論上，粒子數目的大小對最終值的精確度會起到一定作用，當集合中粒子數目比較低的時候，最終值的誤差會較大，反之當集合中粒子數目比較高的時候，同時在粒子數目逼近無窮大時，算法精度最高[14]。因此，當選擇粒子數目的時候，必須更加全面地去思考，如果選擇的粒子數目比較低，那么算法的精度就會降低。但是如果選取過多的粒子，算法在每次迭代過程中要對每個粒子進行運算，導致計算量大幅增加，不能滿足算法的實時性處理需求。

FOX D利用KLD距離采樣對其重采樣部分進行改進，自適應地改變重采樣過程中需要的粒子數目。KL距離具有不對稱性，所以不同的概率密度順序對應著不同的距離值，依此得出的相似度結果并不準確，那么粒子數目的確定就會不合理，對算法性能產生影響。JSD可以克服KLD不對稱性的缺陷，使算法獲得更好的精度。JSD可以計算分布S={s1,s2,s3,…,sn}與分布O={o1,o2,o3,…,on}的相似程度：

(12)

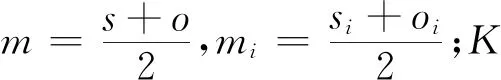
JS距離采樣核心思想是將樣本集合一分為二，利用JS距離計算兩者的相似程度，并且設置兩個門限Sl、Sh。如果JS距離小于低限Sl，那么兩者具有高相似度，有一些非必須粒子存在，此時選取少量粒子進行系統狀態估計，反之JS距離大于高限Sh，說明兩者具有低相似程度，應適當增加粒子總數進行系統狀態估計，粒子數按式(13)計算：

(13)

式中,n為粒子總數。

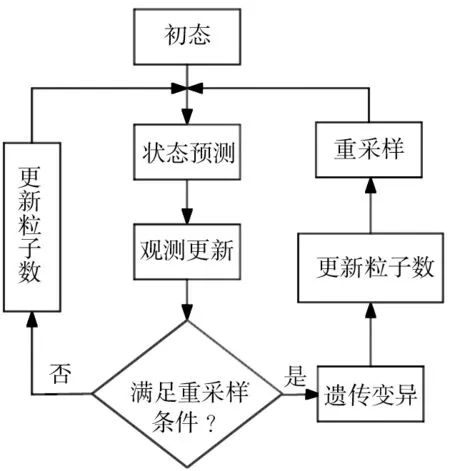
圖1 改進粒子濾波流程圖

圖1是對標準粒子濾波算法進行改進后的算法流程圖。在更新過程之后，判斷是否滿足重采樣的條件，如果條件滿足，則對更新后的粒子集進行變異操作，得到新的粒子集。然后將粒子集合隨機劃分為大小相等的兩個子集，計算它們之間的相似度，根據式(13)調整粒子數，最后進入重采樣過程。

2.3 改進后的蒙特卡羅定位算法

改進算法的具體流程如下：

步驟1 在k=0時，初始化系統。

步驟2 重要性采樣以及權重計算。根據式(8)求取提議分布，并從中采樣粒子。對每個粒子重新分配權重即權重更新。

步驟3 權重歸一化。計算權重總和，進行歸一化運算。

步驟4 重采樣。判斷是否滿足重采樣條件，如果條件滿足，執行步驟5，反之，執行步驟6。

步驟5 根據式(10)劃分高、低權重粒子，低權重粒子按照式(11)的變異概率進行變異操作。根據式(13)自適應改變粒子數目，對高權重粒子和變異產生的粒子進行重采樣，得到新的粒子集合，同時更新權重。執行步驟7。

步驟6 根據式(13)自適應改變粒子數目。

步驟7 狀態估計。把樣本期望值當做此刻k的狀態估計xk。

步驟8 令k=k+1,返回步驟2。

3 實驗結果及分析

3.1 仿真實驗

采用仿真實驗來驗證改進粒子濾波算法的有效性，并將其與利用KL距離采樣的自適應PF算法作對比研究。使用Matlab 7.0軟件進行仿真，機器人系統的狀態模型和觀測模型如式(14)所示[15]。

(14)

其中,系統噪聲ωk～(0,10)，觀測噪聲vk～(0,1)。根據經驗將算法中出現的參數作出如下設定：Sl=0.1，Sh=0.8，初始退火參數設置為0.3，即C=0.3，Pm1=0.1，Pm2=0.01，粒子總數設定為500。在上述參數條件下將采用KL距離采樣的自適應PF算法與研究改進PF算法進行對比研究，每種算法分別進行100次試驗，用誤差均方根值(RMSE)以及有效粒子百分比(NEFF)作為指標對算法性能進行評價。

(15)

(16)

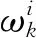
采用KL距離采樣的自適應PF算法[16](圖2～圖8中記為KLPF)以及研究改進PF算法(圖2～圖8中記為AMJSPF)的誤差均方根曲線如圖2所示。由圖2可知，在同等誤差和狀態下，改進PF算法的RMSE低于采用KL距離采樣的自適應PF算法的RMSE。與采用KL距離采樣的自適應PF算法相比，改進算法具有較好的估計精度。不同PF算法粒子數目的變化情況如圖3所示。從圖3中可以看出，兩種算法都可以在線調整采樣粒子數目，相比之下文中改進算法的采樣粒子數目明顯較小。粒子多樣性對比圖如圖4所示。從圖4可以看出,改進算法的粒子多樣性較好。對兩種粒子濾波器的性能進行比較，結果如表1所示。由表1可知，改進算法耗時較少，有較高的有效粒子數，粒子退化問題得以減弱。據此能夠得出研究改進PF算法擁有較高估計精度，減弱了粒子退化問題，減輕了算法計算負擔。

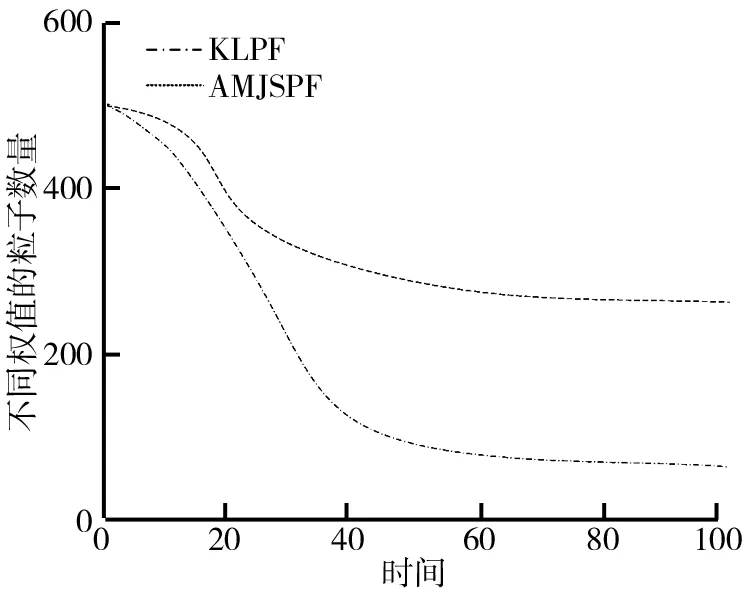
圖4 粒子多樣性對比圖

表1 不同算法的性能對比

3.2 ROS上基于AMLSPF-MCL的機器人定位研究

在室內環境下利用機器人對基于KL距離自適應粒子濾波的蒙特卡羅定位和基于改進粒子濾波的蒙特卡羅定位算法進行對比試驗驗證。實驗采用的平臺為Turtblebot2機器人，其搭載了型號為Hokuyo UTM-30LX的激光傳感器，在配有Windows7操作系統、i7處理器、4G內存的筆記本電腦上運行Liunx(Ubuntu 12.04)操作系統和ROS(hydro)。

利用Bailey發布的開源地圖編輯器設計路標地圖,地圖區域為100 m×100 m,仿真中設定移動機器人從全局坐標(-10,-20)處開始運動,按規劃點運動一周后返回起始點。過程噪聲的方差設定為40，觀測噪聲的方差設定為2，移動機器人運行速度設定為0.35 m/s，粒子的數量設定為2 000，其他參數參照仿真實驗進行設定。

采用KLPF-MCL算法進行定位的結果如圖5所示。由圖5可知，實線代表機器人的真實運動路徑，虛線代表的是估計路徑，由圖5可知此次跟蹤定位失敗。AMJSPF-MCL定位結果如圖6所示。由圖6可知，機器人在采用AMJSPF-MCL算法進行定位時，虛線表示的估計軌跡與實線表示的機器人實際運動軌跡基本一致，跟蹤定位成功。不同定位算法的粒子數目隨著時間變動的改變情況如圖7所示。由圖7可以看出，AMJSPF-MCL算法所需粒子較少，穩定在80。不同算法的定位精度隨時間變動的改變情況如圖8所示。由圖8可以看出，粒子的退化使得KLPF-MCL算法的估計精度降低，最終導致定位失敗；AMJSPF-MCL算法由于有最新觀測數據融入，使得估計精度平均值為19.051 cm，在一定程度上解決了粒子退化問題，可以得到較為精確的定位結果。兩種算法的定位誤差如表2所示。由表2可以看出，AMJSPF-MCL算法的精度比較好，耗時較少。

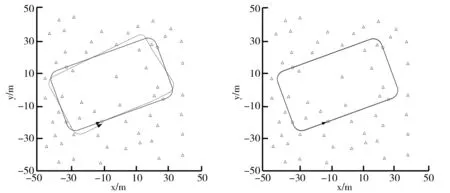
圖5 KLPF-MCL定位結果 圖6 AMJSPF-MCL定位結果

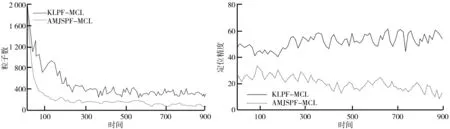
圖7 粒子數隨時間變化情況 圖8 定位精度隨時間變化情況

表2 兩種算法的定位誤差

4 結束語

研究所提的定位算法將先驗概率分布和似然概率分布的混合分布作為提議分布，兩者的混合比例用退火參數進行優化，利用自適應優化機制對退火參數進行動態優化，當前觀測信息融入，對粒子退化現象起到了一定抑制作用。利用JS距離進行采樣，動態調整粒子數量，減小了算法的計算量，增強了算法實時性，算法精度也得到提升。通過遺傳變異操作，粒子多樣性得到一定程度的保持。經過實驗，改進算法被證明是有效的。研究中JS距離閾值所用的門限值沒有進行嚴密的分析論證，并且在定位的過程中忽略了車輪打滑等影響算法精度的因素，后期將對算法繼續進行完善。