基于改進蟻群算法的自動駕駛汽車自主避障路徑優化分析

李詩玄

摘 要：為了進一步提高自主駕駛汽車真實動態環境下快速、準確的自主避障能力，提出了一種基于粒子群參數優化（PSO）的改進蟻群算法（AC）模型實現了對自動駕駛汽車在自動避障時規劃路徑的全局快速優化分析。首先，建立了自駕車輛的自主避障路徑規劃模型;其次，利用PSO中粒子間的協作和信息共享模式搜索全局信息;再次，利用全局信息更新策略優化AC的路徑搜索能力;最后，采用PSO和AC融合算法求解出最佳的避障路徑。仿真結果表明，粒子群算法對蟻群算法模型進行了改進，從而實現了對自駕車輛自主避障路徑的快速、準確的實時動態規劃。

關鍵詞：自主駕駛汽車;路徑規劃;蟻群算法;粒子群優化;自主避障

Abstract：In order to further improve the accurate response and fast response ability of autonomous obstacle avoidance in real dynamic environment， an improved AC （ant colony algorithm） model based on PSO （Particle Swarm Optimization） is proposed to realize the global and fast optimization analysis of autonomous obstacle avoidance path planning for self-driving vehicles. Firstly， an autonomous obstacle avoidance path planning model for self-driving vehicles is established; secondly， the global pheromone is searched by using the cooperation and information sharing mode between particles in PSO; thirdly， the global pheromone updating strategy is used to optimize the path searching ability of AC; finally， an innovative way of integrating PSO and AC is used to obtain the optimal path of autonomous obstacle avoidance for self-driving vehicles. The simulation results show that the AC model is improved by PSO to realize the fast and accurate planning of autonomous obstacle avoidance path for self-driving vehicles.

Key words： self-driving vehicle; path planning; ant colony algorithm; particle swarm optimization; autonomous obstacle avoidance

自動駕駛車輛的自主避障已經成為無人駕駛車輛領域的熱門話題[1]。為了有效保護自動駕駛車輛行駛狀態下的人身和財產安全，許多研究者將人工智能技術和算法應用于自駕車輛的自主避碰和動態路徑規劃問題之中[2]。其中，蟻群算法在路徑規劃的應用方面效果尤為突出[3]。

然而，在現實生活中，自動駕駛車輛的自主避障技術尚未得到相關立法和工程技術行業的廣泛推廣[4]，其主要原因是相關技術尚未達到成熟和可控的水平。蟻群算法是由意大利學者Dorigo、Maniezzo等人于20世紀90年代首先提出來的。他們發現蟻群在覓食過程中，個體螞蟻的行為相對簡單，但是螞蟻群體行為卻具有一定的智能性。在覓食時，多樣性使螞蟻不會走進死胡同而無限循環，是一種創新能力;正反饋使優良信息保存下來，是一種學習強化能力。兩者的巧妙結合使智能行為涌現，如果多樣性過剩，系統過于活躍，會導致過多的隨機運動，陷入混沌狀態;如果多樣性不夠，正反饋過強，會導致僵化，當環境變化時蟻群不能相應調整。同時，蟻群算法本身存在諸如收斂響應時間長，易于進入局部最優解的問題[5]。單一算法無法獨立完美地解決自動駕駛車輛自主避障路徑規劃的實際應用問題?；诖吮尘埃喾N智能算法的結合已成為解決自動駕駛車輛自主避障問題的路徑規劃的發展趨勢。因此，下面本文介紹一種基于粒子群優化的改進蟻群算法。

2.自動駕駛車輛自主避障路徑技術路線優化的建立

自動駕駛車輛的自主避障對實時響應和的可控性有很高的要求，因此路徑規劃評估十分重要。結合PSO算法和AC算法各自的優點，圖1給出了自動駕駛車輛自主避障路徑規劃優化設計的技術設計路線：

自駕車輛自主避障路徑的具體技術路線優化：

1.使用PSO算法，構造時空的粒子集合：Ω（pi）（xi，yi，zi，tpi）;

2.建立粒子動態搜索模式，優化粒子適應度函數;

3.通過適應度函數動態調整全局信息素（使用循環迭代）;

4.建立蟻群算法，找出最短路徑函數（建立信息素更新方法）;

5.在時空中增加全局信息素干預;

6.通過全局范圍信息素的積累和路徑優化的迭代工作，得到了自駕車輛自主避障行為的規劃路徑。

3.基于PSO的改進蟻群自主避障路徑優化模型

3.1基于PSO的適應度函數模型

PSO是一種基于種群的隨機優化控制技術，受種群行為特征的啟發，用于解決優化問題。每個優化問題的潛在解決方案可以被認為是n維搜索空間中的一個點，稱為“粒子”。所有粒子都具有由目標函數確定的適應度值，并且每個粒子具有確定其方向和距離的速度。然后粒子跟隨當前最優粒子在解空間中搜索。

每個粒子可以被視為n維搜索空間中的搜索個體。粒子的當前位置是相應優化問題的備選解決方案。粒子的飛行過程是個體的搜索過程。粒子的飛行速度可以根據粒粒子向自身的歷史最佳位置和鄰域或整個群體的歷史最佳位置聚集來進行。粒子只有兩個屬性：速度和位置，速度代表粒子的運動速度，位置代表粒子的運動方向。每個粒子獨立搜索的最優解決方案稱為獨立極值，粒子群中的最優獨立極值是當前的全局的最優解。速度和位置不斷迭代和更新。最終，獲得滿足終止條件的最優解。

3.1.1 PSO算法的初始化

PSO用于通過粒子間的協作和信息共享獲得滿足自行駕駛車輛自主避障的路徑規劃優化要求時空中最佳的定位點。結合算法更能有效提高求解過程中的收斂速度和最優解精度，找到最優調度方案[6，7]。

粒子的速度矢量和當前時空位置用公式（1）和（2）表示。

（1）

（2）

在公式（1）和（2）中，Vi+1是粒子的速度矢量，Pi+1是時間t時粒子的位置，pbesti代表單粒子的最佳位置，gbesti代表整個群體的實際最佳位置，c0，c1，c2代表路徑規劃過程中粒子群的調整系數，c0是0到1之間的隨機數，c1，c2是0到2之間的隨機數. Vi是Vi+1，pbesti-Pi和gbesti-Pi之間的向量和，代表粒子速度的更新受當前速度，感知模式和群體信息的影響。

3.1.2 適應性函數的意義

在自動駕駛車輛自主避障路徑優化的背景下，PSO的動態響應適應度函數定義如下[8]。

（3）

在公式（3）中，在時間t，（xp，yp，zp）是粒子的空間坐標，（xS，yS，zS）是起點坐標，（xD，yD，zD）是結束點坐標。

表示從當前位置到終點的p粒子的估計值。 ? ? ? ? ? ? 表示從起點到當前位

置的距離之和， ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 。 Ob代表預測障礙信息量。當 ? ? ? ? ? ? ? ? ? ? ?時，Ob很清晰;當 ? ? ? ? ? ? ? ? ? ? 時，Ob比較清晰;當 ? ? ? ? ? ? ? ? ? ? ? ? ? ?時，Ob為一般清晰;當 ? ? ? ? ? ? ? ? ? ? ? ? ? 時，Ob相對模糊。

3.2基于AC的全局信息素更新

蟻群算法的基本原理來源于自然界中螞蟻覓食的最短路徑原理。當螞蟻在尋找食物來源時，它們會在它們所經過的路徑中釋放信息素，這是螞蟻在覓食過程中進行種群交流的一種特性，因此在一定范圍內的其他螞蟻可以檢測并因此影響它們未來的行為。當越來越多的螞蟻通過某些路徑時，它們會留下越來越多的信息素，導致信息素濃度增加，從而選擇該路徑的螞蟻的概率就會更高，這也會導致在該路徑上的信息素濃度增強。該選擇過程稱為螞蟻的自催化行為。螞蟻行走路徑用于表示待優化問題的可行解，整個蟻群的所有路徑構成了待優化問題的解空間。路徑較短的螞蟻會釋放更多的信息素。隨著時間的推移，在較短路徑上累積的信息素濃度逐漸增加，選擇該路徑的螞蟻數量也在增加。

3.2.1 AC的初始化

螞蟻之間的信息傳遞是通過稱為信息素的物質實現的。通常，AC的信息素累積過程受路徑規劃更新過程中信息量的影響[9]。

路徑優化過程中AC的信息更新方法如公式（4）所示。

（4）

在公式（4）中， ? ? ? ? ?表示循環中路徑ij上的信息量的總增量; ρ表示信息的揮發程度，范圍從0到1; ? ? ? ? ? ?表示在此循環中螞蟻k在路徑ij上離開的信息增量; Cf表示在該循環中螞蟻k在路徑ij上留下的信息量的增量相關系數。

3.2.2 全局信息素的動態更新策略

根據PSO在全局時空中的適應性函數，在AC的迭代過程中調整了全局情況下的信息素分布和積累[10]。

通過調整Cf，可以實現信息素累積的全局調度。 Cf的具體形式如下所示。

（5）

在公式（5）中，RBest表示最優規劃路徑數據，f（pi）min表示粒子群適應性函數的最小值，f（pi）max表示粒子群適應性函數的最大值。

4.仿真分析

為了驗證基于PSO優化AC的自動駕駛車輛自主避障路徑優化問題的可行性，從規劃路徑自身優化程度和路徑規劃的時效性兩個維度進行了仿真驗證。

4.1規劃路徑模擬

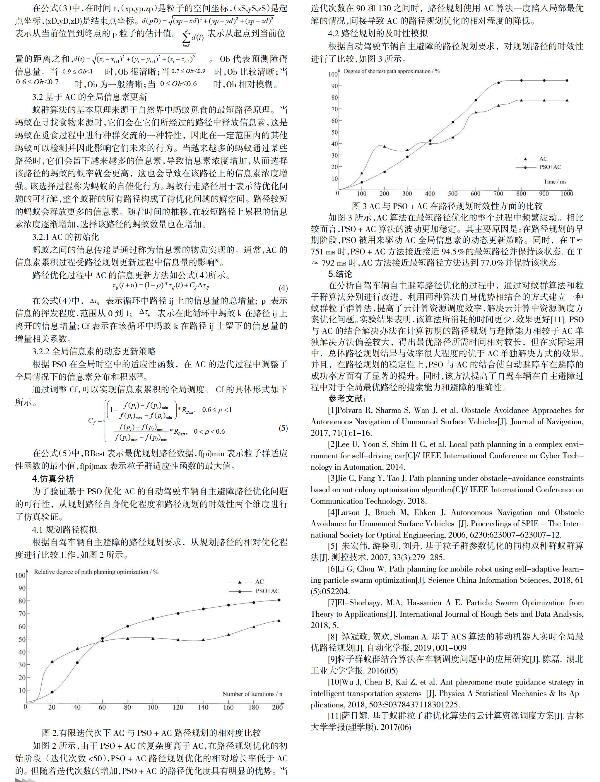
根據自駕車輛自主避障的路徑規劃要求，從規劃路徑的相對優化程度進行比較工作，如圖2所示。

如圖2所示，由于PSO + AC的復雜度高于AC，在路徑規劃優化的初始階段（迭代次數<50），PSO + AC路徑規劃優化的相對增長率低于AC的。但隨著迭代次數的增加，PSO + AC的路徑優化度具有明顯的優勢。當迭代次數在90和130之間時，路徑規劃使用AC算法一度陷入局部最優解的情況，間接導致AC的路徑規劃優化的相對程度的降低。

4.2路徑規劃的及時性模擬

根據自動駕駛車輛自主避障的路徑規劃要求，對規劃路徑的時效性進行了比較，如圖3所示。

如圖3所示，AC算法在最短路徑優化的整個過程中頻繁波動。相比較而言，PSO + AC算法的波動更加穩定。其主要原因是：在路徑規劃的早期階段，PSO被用來驅動AC全局信息素的動態更新策略。同時，在T≈751 ms時，PSO + AC方法接近接近94.5%的最短路徑并保持該狀態。在T ≈ 792 ms時，AC方法接近最短路徑方法達到77.0%并保持該狀態。

5.結論

在分析自駕車輛自主避障路徑優化的過程中，通過對蟻群算法和粒子群算法分別進行改進，利用兩種算法自身優勢相結合的方式建立一種蟻群粒子群算法，提高了云計算資源調度效率，解決云計算中資源調度方案優化問題。實驗結果表明，該算法所消耗的時間更少，效果更好[11]。PSO與AC的結合解決辦法在計算初期的路徑規劃與避障能力相較于AC單獨解決方法偏差較大，得出最優路徑所需時間相對較長，但在實際運用中，總體路徑規劃結果與效率很大程度的優于AC單獨解決方式的效果。并且，在路徑規劃的穩定性上，PSO與AC的結合使自動避障車在避障的成功率方面有了顯著的提升。同時，該方法提高了自駕車輛在自主避障過程中對于全局最優路徑的搜索能力和避障的準確性。

參考文獻：

[1]Polvara R， Sharma S， Wan J， et al. Obstacle Avoidance Approaches for Autonomous Navigation of Unmanned Surface Vehicles[J]. Journal of Navigation， 2017， 71（1）：1-16.

[2]Lee U， Yoon S， Shim H C， et al. Local path planning in a complex environment for self-driving car[C]// IEEE International Conference on Cyber Technology in Automation. 2014.

[3]Jie C， Fang Y， Tao J. Path planning under obstacle-avoidance constraints based on ant colony optimization algorithm[C]// IEEE International Conference on Communication Technology. 2018.

[4]Larson J， Bruch M， Ebken J. Autonomous Navigation and Obstacle Avoidance for Unmanned Surface Vehicles[J]. Proceedings of SPIE - The International Society for Optical Engineering， 2006， 6230：623007-623007-12.

[5]朱宏偉， 游曉明， 劉升. 基于粒子群參數優化的同構雙種群蟻群算法[J]. 測控技術， 2007， 33（3）：279-285.

[6]Li G， Chou W. Path planning for mobile robot using self-adaptive learning particle swarm optimization[J]. Science China Information Sciences， 2018， 61（5）：052204.

[7]El-Shorbagy， M.A， Hassanien A E. Particle Swarm Optimization from Theory to Applications[J]. International Journal of Rough Sets and Data Analysis， 2018， 5.

[8]譚冠政， 賀歡， Sloman A. 基于ACS算法的移動機器人實時全局最優路徑規劃[J]. 自動化學報， 2019，001-009

[9]粒子群蟻群結合算法在車輛調度問題中的應用研究[J]. 陳磊. ?湖北工業大學學報. 2016（05）

[10]Wu J， Chen B， Kai Z， et al. Ant pheromone route guidance strategy in intelligent transportation systems[J]. Physica A Statistical Mechanics & Its Applications， 2018， 503：S0378437118301225.

[11]薩日娜. 基于蟻群粒子群優化算法的云計算資源調度方案[J]. 吉林大學學報（理學版）. 2017（06）