基于PID數字控制器的爐溫控制系統分析與設計

朱 芳，李素文，陳得寶，李 崢

(淮北師范大學物理與電子信息學院，安徽 淮北 235000)

1 研究背景

近年來，隨著脈沖技術、數字式元件部、數字計算機，特別是微處理器的發展[1]，以及數字式通信線路的大量使用，數字控制器在許多場合代替了模擬控制器，使絕大部分的精密控制系統和復雜的過程控制走向數字化。溫度是工業過程控制中的主要參數之一，廣泛應用的工業電爐是工業生產的首選，電爐的溫度決定產品的質量[2]。因此，對溫度控制的要求非常高。由于爐溫具有較大的慣性，并且溫度上升具有滯后性，本身時間常數大，爐溫變化較慢[3]，采用連續控制方式不能解決控制精度與動態性能的矛盾，因此，建立加入采樣開關的離散控制系統，可進一步提高系統的穩定性。

本文首先建立了具有零階保持器的爐溫離散控制系統，并對其進行穩定性和時域分析；其次，在系統穩定的基礎上對其進行PID數字控制器校正，采用二級臨界擴充比例法選取合適的PID參數，提高系統的穩定性和動態性能；從而在實際生產中加強系統本身的溫度控制能力，節省人力物力。

2 離散系統的數學模型

2.1 爐溫控制系統的分析

工業爐溫控制系統中爐子的滯后時間大約為數秒至數十秒，其慣性時間常數T可高達千秒以上，而電機的機電時間常數Tm與它們比起來小得可以忽略。常用爐溫控制系統的原理框圖如圖1所示。

圖1 爐溫控制系統原理框圖

爐溫的誤差信號經放大后驅動電動機去調整燃料閥門的開度以控制爐溫。若系統的開環放大倍數很大，系統對誤差信號將非常敏感。當爐溫較低時，電動機將迅速旋轉，開大閥門，給爐子供應更多的燃料。由于爐子本身的時間常數較大，導致爐溫上升緩慢。當檢測的爐溫與給定值相同時，電機控制閥門的開度非常大，燃料持續供應，爐溫繼續上升，造成超調，此時電動機又將反方向旋轉[4]。根據同樣的道理，又會造成爐溫的反方向超調，從而引起爐溫大幅度的振蕩，甚至使系統不穩定。根據爐溫控制系統原理可得系統結構如圖2所示。

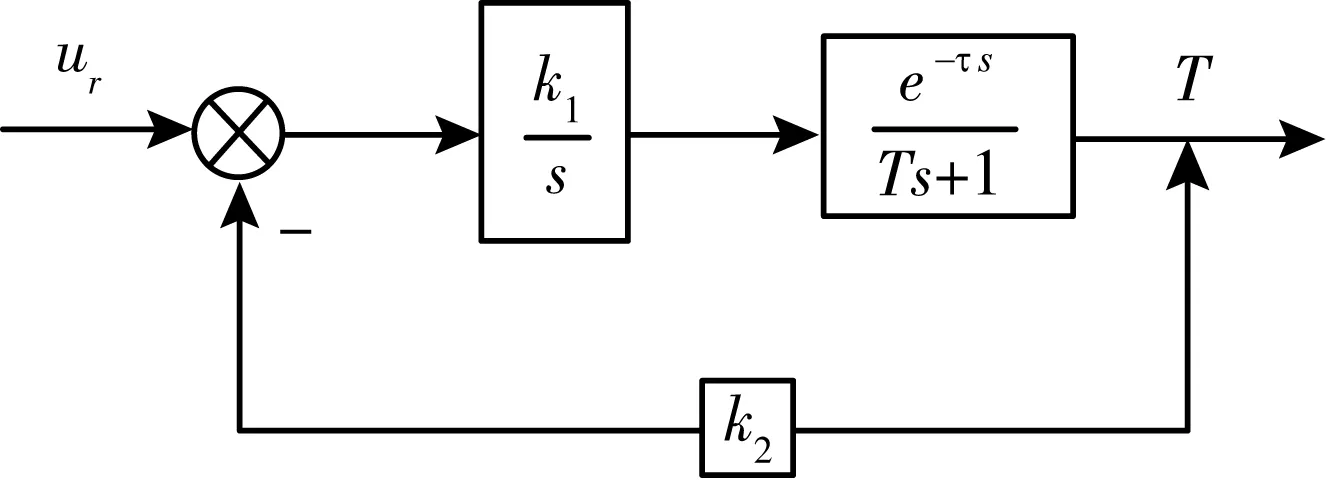
圖2 爐溫控制系統結構圖

k1k2為系統開環增益，τ為爐溫遲滯時間常數，T為慣性環節時間常數。取系統的相角裕度γ=30°，若τ=10 s，T=100，則系統開環增益k1k2≤0.017；若τ=0,T=10，則k1k2≤0.029；若τ=0,T=1，則k1k2≤3。這說明T很大又存在滯后時，為了得到好的動態品質，開環增益只能大大減小，則穩態誤差會增大。此時若附加校正，由于T太大，校正裝置的時間常數也應很大，難以實現。

2.2 爐溫離散系統的數學模型

為了解決上述問題，可以在誤差信號和電機之間加一個采樣開關，建立爐溫離散控制系統。采樣開關進行周期性閉合和斷開。當爐溫出現誤差時，誤差信號只有在開關閉合時才能傳遞，使電機旋轉，進行爐溫調節。當開關斷開時，電動機立刻停下來，閥門位置固定，讓爐溫自動變化，直到下一次采樣開關閉合，再根據爐溫的誤差進行調節。由于電動機時轉時停，爐溫大幅度超調現象將受到抑制，即使采用較大的開環放大倍數，系統仍能保持穩定。加入零階保持器的線性離散爐溫控制系統結構，如圖3所示。

圖3 線性離散爐溫控制系統結構圖

當系統的開環增益k1k2=0.2，滯后系數τ=10，慣性系數Ta=120，采樣周期T=10 s時，離散控制系統的開環脈沖傳遞函數為：

(1)

由式(1)知，離散系統有3個開環極點、1個開環零點。

3 離散控制系統的分析

3.1 離散控制系統的穩定性分析

對于線性離散系統，時域中的數學模型是線性定常差分方程，z域中的數學模型是脈沖傳遞函數。由s域到z域的映射關系知，線性定常離散系統穩定的充要條件是離散系統特征方程的全部特征根均分布在z平面上的單位圓內[5]。離散系統的穩定性與系統的開環增益有關，可以根據開環脈沖傳遞函數繪制系統的根軌跡，確定系統穩定時開環增益的取值范圍(圖4)。或者繪制系統的Bode圖，使幅值裕度和相角裕度均大于零的范圍，則系統穩定(圖5)。

圖4是系統的開環增益從0變化到無窮時，閉環極點的根軌跡。由圖4知，使系統穩定的開環增益取值范圍為(0,0.702)。相較于連續系統，此時離散系統的開環增益得到大大提高，有利于改善系統的穩態性能，減少穩態誤差。由圖5可知，系統穩定時的相角裕度為15.8°，小于通常所達到較好動態品質的30°，可對系統進行改善。

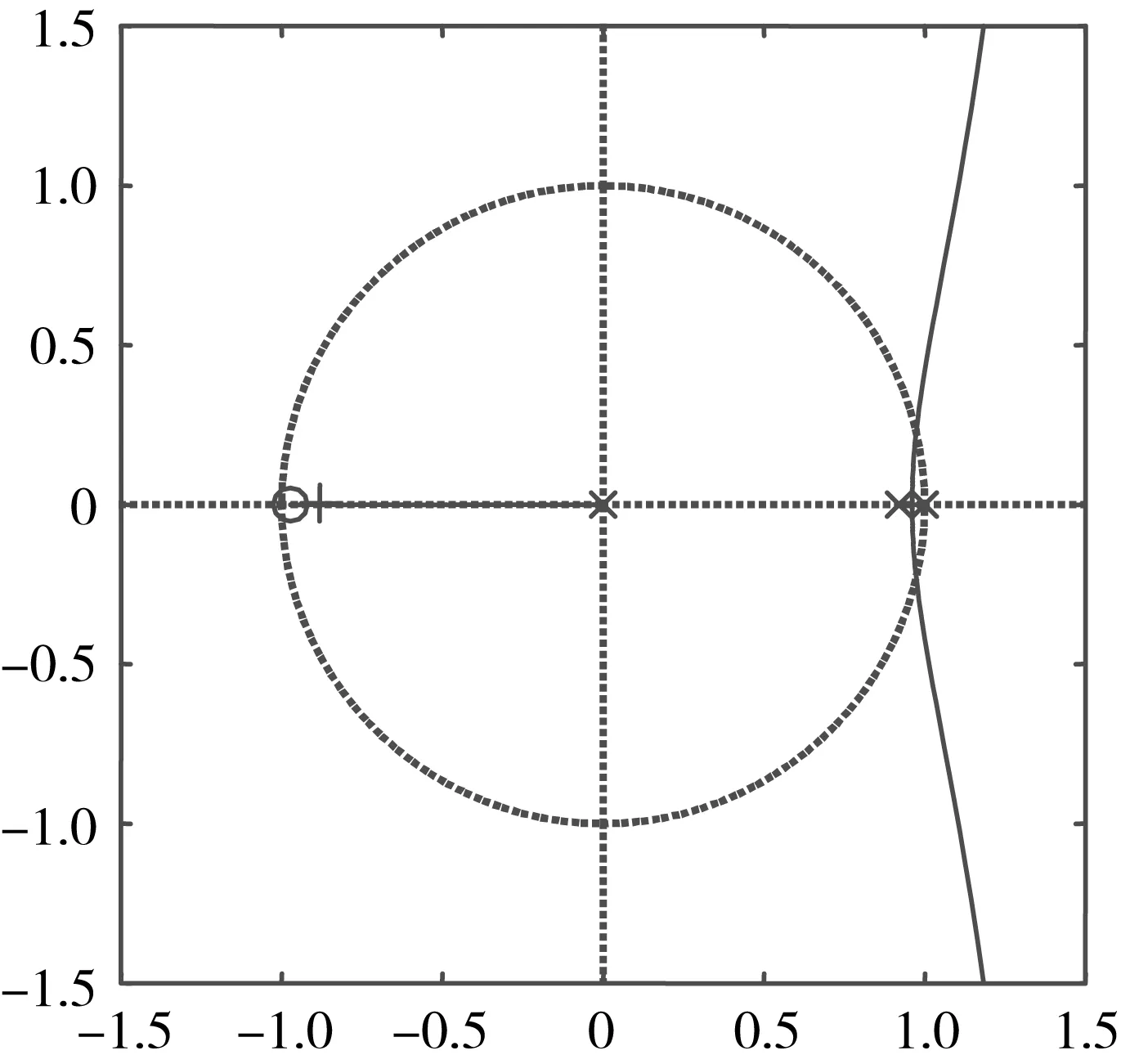
圖4 爐溫控制系統的根軌跡

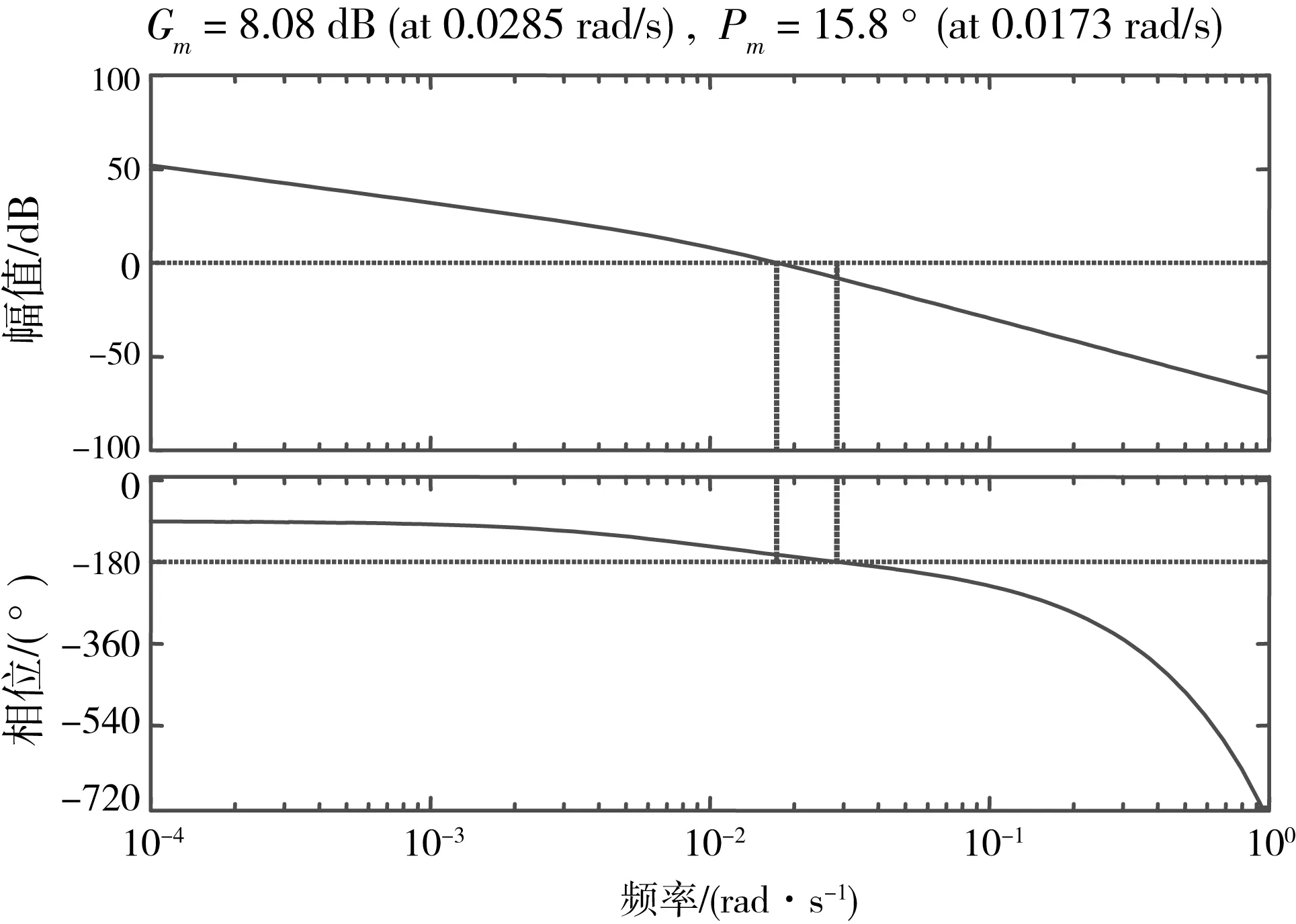
圖5 爐溫控制系統的Bode圖

3.2 離散控制系統的時域分析

應用z變換法分析線性定常離散系統的動態性能，通常有時域法、根軌跡法和頻域法，其中時域法最簡便[7]。下面主要分析單位階躍信號輸入下采樣周期和開環增益對系統穩定性和動態性能的影響。

采樣周期為10 s，開環增益為0.08、0.1、0.2、0.8時，系統的單位階躍響應如圖6所示。

圖6 k1k2為0.08、0.1、0.2、0.8時系統的單位階躍響應

由圖6可知，開環增益越大，系統單位階躍響應曲線振蕩越劇烈，動態性能也依次變差，甚至由原來的穩定變為不穩定。因此，采樣周期一定時，改變開環增益會使離散系統的穩定性發生改變。

當開環增益取0.1，采樣周期取10、50、100、200時，系統的單位階躍響應如圖7所示。

由圖7知，當開環增益一定時，隨著采樣周期的增大，系統的單位階躍響應曲線階梯越來越明顯。雖然調節時間有所減少，但超調量逐漸增大，振蕩次數越來越多。因此，采樣周期越長，信息丟失的越多，對離散系統的穩定性及動態性能均不利。

圖7 采樣周期為10、50、100、200時系統的單位階躍響應

4 基于PID數字控制器的設計與仿真

4.1 PID數字控制器的設計

PID控制是工業過程控制中應用最廣泛的經典控制器。它是根據系統偏差的比例、微分、積分進行線性組合的一種控制方式[8]，對積分項和微分項應用向后差分法，其離散化的數字PID控制器輸出形式為：

(2)

其中，KP是PID的比例系數；KI是PID的積分系數；KD是PID的微分系數。離散系統某時刻的輸出不僅與輸入有關，還與前一刻的輸出有關。PID數字控制器的脈沖傳遞函數為輸出與離散偏差之比，其形式為：

(3)

式(3)為PID控制器的脈沖傳遞函數形式。

4.2 PID數字控制器參數整定方法

PID數字控制器需要確定的參數包括比例系數、積分系數、微分系數和采樣周期。由3.2知，采樣周期必須滿足香農定理，并且受到滯后和控制精度的制約。工程上根據經驗溫度的采樣周期一般為10～20 s或等于純滯后時間。PID參數整定的方法有很多，主要有兩類：①理論計算法。根據數學模型，計算數字控制器的參數。此種方法的缺點是所得參數必須經過工程實際進行調整。②工程整定法。包括Ziegler-Nichols整定法、擴充臨界比例度法、曲線衰減法等。其特點是按照工程經驗公式對控制器參數進行確定，方法簡便、易于掌握。本文采用二級擴充臨界比例度法調整PID數字控制器的參數。二級擴充臨界比例度法是令PID控制器的積分項和微分項等于零，求出系統階躍響應為等幅振蕩時的比例系數KP和振蕩周期Tk。為了得到更精確的比例系數，對KP進行二級步長搜索，再根據經驗公式求出控制度和對應的積分、微分系數。流程圖如圖8所示。

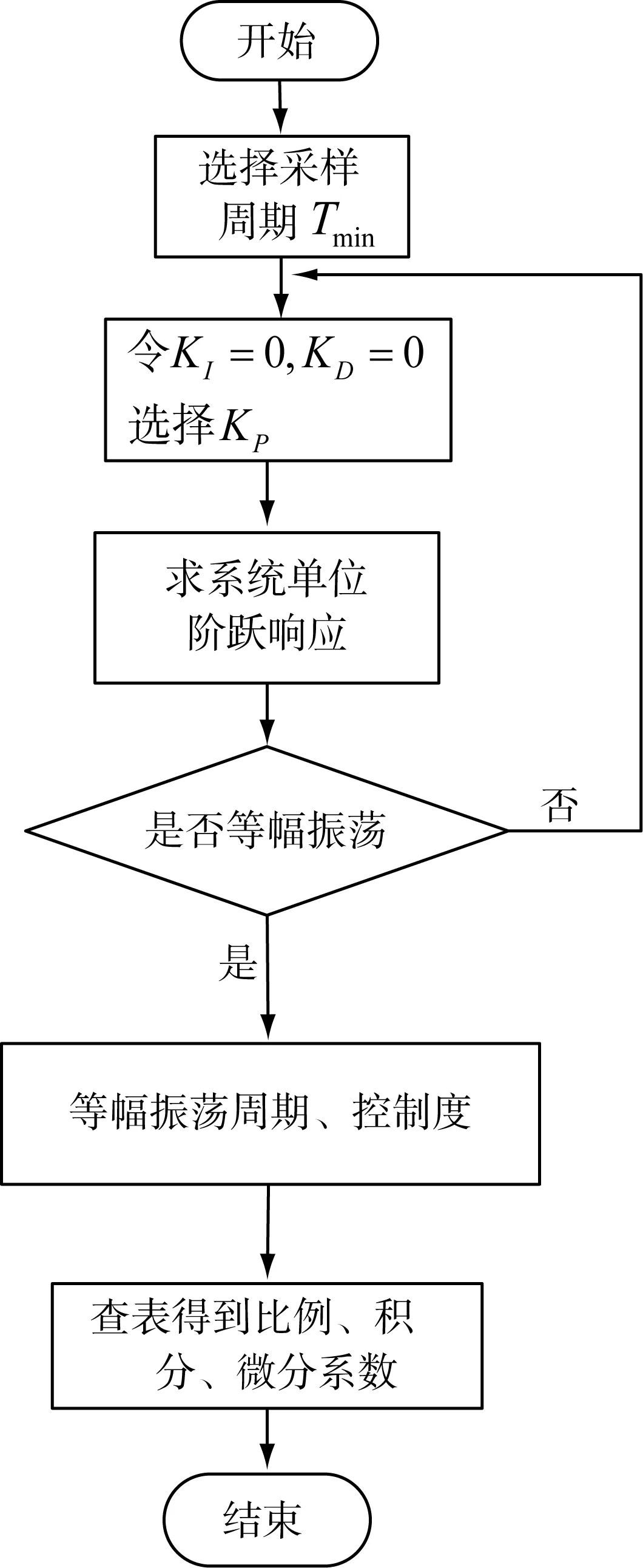
圖8 臨界擴充比例度法的PID參數整定

具體步驟如下：

步驟1 選擇最小采樣周期Tmin=10 s(采樣周期等于純滯后時間)，令KI=0，KD=0。

步驟2 根據系統的根軌跡選擇KP的初始值，求系統的單位階躍響應曲線。

步驟3 以0.1為步長，逐步改變KP的值，獲得系統單位階躍響應，直到出現不等幅振蕩。

步驟4 為了精確臨界比例，以0.01為步長，改變為KP的值，判斷是否出現等幅振蕩。

4.3 實驗仿真與結果

線性離散系統的設計方法主要有模擬化設計和離散化設計兩種。模擬化設計方法，把控制系統按模擬化進行分析，求出數字部分的等效連續環節，然后按連續系統理論設計校正裝置，再將該校正裝置數字化。離散化設計方法，又稱直接數字設計法，把控制系統按離散化進行分析，求出系統的脈沖傳遞函數，然后按離散系統理論設計數字控制器[4]。本文主要采用直接數字設計方法，因為該設計方法簡便，更具有一般性，適合更復雜的系統。因此，根據離散系統的數學模型和PID數字控制器，建立Simulink仿真模型如圖9所示。

圖9 爐溫離散控制系統的Simulink模型

通過調節PID控制器的參數，首先確定KI=0，KD=0時，系統出現等幅振蕩的單位階躍響應(圖10)。最后將已確定參數的PID數字控制器進行設置，獲得校正后系統的單位階躍響應如圖11所示。

圖10 等幅振蕩

圖11 加入PID數字控制器的單位階躍響應

5 結語

工業爐溫控制系統具有多樣性和復雜性，不同型號的爐子具有不同的傳遞函數和數學模型，采用Matlab-Simulink軟件對其進行仿真分析與設計是十分簡單、高效的。本文所設計工業爐溫系統具有較大的慣性和滯后特性，極大地制約了溫度調節的精度。通過研究發現，建立爐溫離散控制系統能夠更好地消除動態過程出現的反超調情況，改善系統的穩定性和動態性能。另外，為了符合實際需求，設計了PID數字控制器，并對控制器參數進行二級擴充臨界比例度法整定，實現對溫度變化的精確穩定控制，減小溫度調節時間，具有較強的實用價值。