初中數學課堂對學生創新性思維的培養

遼寧省撫順市東洲區教師進修學校附屬中學 張擁軍

所謂創新性思維，其具體內涵指的是在真實學習的過程中，進行學習的個體能夠充分發揮“認識”的意義，能夠打破自身固有的邏輯思維方式，從而以豐富多樣的、新穎的思路作為切入點展開思考與分析，進而達到有效理解和掌握的目的。創新性思維對于學生將來的專業領域或者其他活動，都能夠起到提高解決問題的效率的作用，由此可見創新性思維培養的重要意義所在。以下，筆者就此同時結合本階段學生對知識的認知規律以及數學學科自身的特征進行綜合性的考量，并分三個方面對初中數學課堂創新性思維的培養教學作如下詳細的總結與歸納。

一、靈活利用問題啟發，引導學生思維積極性

亞里士多德曾經針對“創新思維”做過明確的定義，他認為：“創新思維是通過疑問與驚奇開始的，具備了疑問，才能進行更加深入的思考，才能夠發現問題。”由此可見，對于學生創新性思維的培養教學，應當首先從對學生發現問題、提出問題的引導方面入手，從而以此激發其學習思維的積極性，為其創新思維的形成做好鋪墊。對此，課堂教學可以通過問題啟發的方法來進行，即將相關知識的教學內容通過問題的形式呈現，以此逐步實現調動學生思維的目的，為教學目標的實現提供保障。

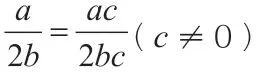
二、注重利用例題訓練，拓展學生思維靈活性

在數學課堂當中，創新性思維主要體現在解題的過程當中，因此，我們還應當積極地利用例題解題的方式對學生的創新思維進行鍛煉培養。其中，應當注意的是，對于創新性思維來說，解題不在于數量，而在于學生對解題方法的掌握。故而，我們應當注重通過一題多解、一題多變等方式對學生展開引導，使之在此過程中思維的靈活性得到極大的拓展，為創新思維的形成作出良好鋪墊。

例如：“兩個連續的奇數，它們的積是323，那么這兩個數是多少？”多數學生則會設定較小的奇數為x，那么根據連續奇數的性質，另外一個就是x+2，由此可以得出方程x（x+2）=323，并通過解方程得出相關答案。在這一基礎上，筆者提示學生，是否還能夠用其他的方法來求解呢？此時，當學生在思考到一定的程度后，筆者便提示學生上一種方法設定的是較小的奇數，那么設定較大的數是否同樣能

夠得出答案呢？由此，讓學生在這一思路下自主進行探究和思考，而學生便可以根據前一種方法逆向思考，根據連續奇數的特征，得出方程：。這一環節的誘導大大拓展了學生思維的靈活性，為其創新性思維的形成提供了良好的前提條件。

三、滲透數學思想方法，促進學生思維創造性

在數學課堂當中，對學生創新性思維的培養，還可以通過滲透數學思想方法的方式來對學生加以引導，即在教學中指導學生深入挖掘數學知識中所蘊含的數學內涵、思想，使之能夠從本質上認識到數學知識規律，增強其對知識學習的獨立性思考與分析，從而為其創造性思維的產生提供有力的保障。

我們仍以《分式的基本性質》相關內容的教學為例，筆者通過向學生灌輸“類比思想”的方法，對課堂展開了教學。如筆者利用“分數的基本性質”為類比，將兩者的性質內涵同時列出，讓學生觀察得出兩者的區別在于分數只能是不為0 的“數”，而分式可以是不為0的“數”或“式”。之后，在這一類比之下，筆者讓學生以此為基礎，嘗試用相關式子對分式的基本性質進行表示。諸如此類，學生在掌握了數學類比思想的方法和模式之后，對數學相關知識點的規律和邏輯又有了更深一層的認識，從而為其在今后的學習中發現新知、創新學習方法等提供了重要的思路，大大推進了課堂目標的實現。

總而言之，創新性思維的培養，關鍵在于對學生固有學習思維模式的轉變，只有讓學生具備敢于顛覆思維定勢桎梏的學習品質，其創新性思維的形成才能得到良好的保障。