超大跨度部分地錨式斜拉橋抗震性能研究

(浙江工業大學 建筑工程學院，浙江 杭州 310023)

自1956年世界第一座現代斜拉橋——瑞典的斯特洛姆桑特橋建造以后，斜拉橋以其較強的跨越能力和良好的經濟性能在400～1 000 m跨徑范圍得到了廣泛的應用。本世紀以來，蘇通長江大橋(1 088 m)、香港昂船洲大橋(1 018 m)和俄羅斯海參威Russky島大橋(主跨1 104 m)的相繼建成實現了斜拉橋主跨超千米的突破。為適應世界橋梁工程的跨海聯島工程建設的需要，斜拉橋的跨徑仍將持續增大[1]。當前，大跨度斜拉橋基本都采用斜拉索全自錨體系。全自錨式斜拉橋主跨進入超千米領域后，塔梁交界處主梁承受的過大軸向壓力以及由此產生的主梁屈曲問題，已成為限制斜拉橋跨徑進一步增大的關鍵問題[1]。為解決塔梁交接處主梁軸壓過大問題，丹麥Gimsing[2]和法國Muller[3]等學者研究相繼提出了部分地錨式斜拉橋結構體系，該體系將邊跨部分斜拉索集中錨固于地錨上，中跨跨中部分區段采用纜索吊裝施工，該部分斜拉索索力水平分力轉化為主梁中的拉力，從而減小塔梁交接處主梁承受的軸向壓力。已有研究表明：部分地錨斜拉橋的結構設計和施工都是可行的，且相對于同跨徑全自錨式斜拉橋具有主梁壓力減小、穩定性提高和結構剛度增大等優點[4]。

近年來，國內外學者對部分地錨斜拉橋的結構體系[4-5]、靜力性能[6-9]、經濟性能[10]、動力特性[11]以及抗風性能[12-13]等方面開展了大量的研究工作，但對重要的結構抗震問題基本未涉及。眾所周知，大跨度部分地錨式斜拉橋是一種柔性結構體系，水平剛度小，地震作用下的結構性能是其設計需要考慮的重要因素。為此，筆者以一主跨1 400 m的部分地錨式斜拉橋設計方案為背景，采用反應譜法和時程分析法進行E1和E2地震作用下的結構地震反應分析，揭示其抗震性能特點以及結構非線性對地震反應的影響，在此基礎上通過與相同主跨的全自錨式斜拉橋方案地震反應的對比分析，從抗震性能角度探討部分地錨式斜拉橋結構應用于超千米主跨橋梁的適用性。

1 主跨1 400 m部分地錨式斜拉橋設計方案簡介

如圖1所示為主跨1 400 m的部分地錨式斜拉橋設計方案[14]，采用全漂浮體系，橋跨布置為444+1 400+444 m，邊主跨徑比為0.317，兩側邊跨內距離邊墩144 m處各設置一個輔助墩；中跨自錨梁段長度1 000 m，跨中400 m梁段通過邊跨拉索錨固在地錨上；主梁為高4.5 m和寬41 m的扁平鋼箱梁，跨高比為311，跨寬比為34.1，寬高比為9.1；橋塔為A型橋塔，采用鋼筋混凝土結構，塔高357 m，其中橋面以上高度為287 m，高跨比為0.205。橋塔分別在塔梁連接處設置下橫梁，并在拉索錨索區下端設置上橫梁；斜拉索采用空間傾斜扇形雙索面布置，共計304 根(38×2×4)，其中兩側邊跨共計52(13×4)根斜拉索錨于地錨上。

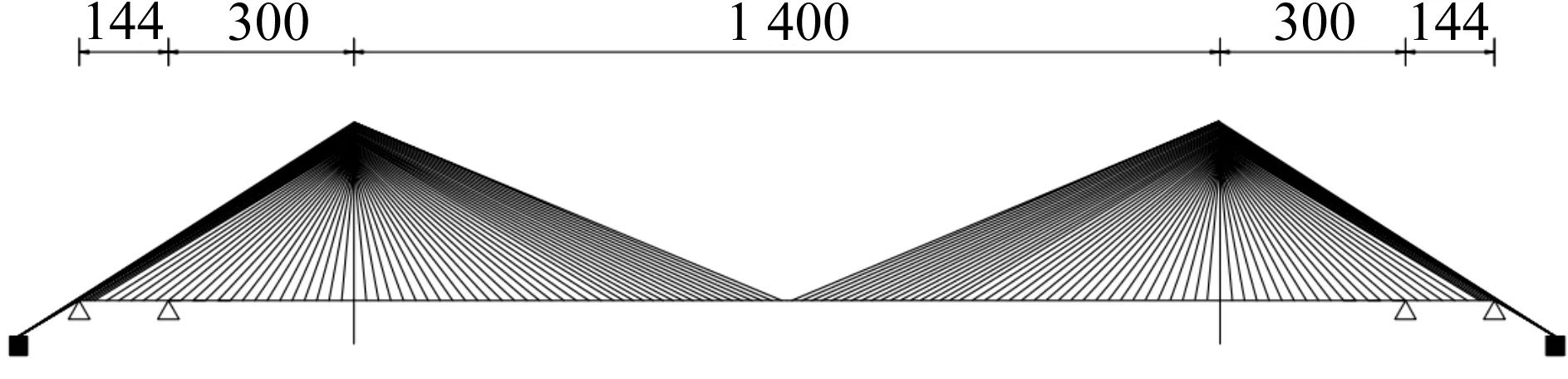
圖1 主跨1 400 m部分地錨式斜拉橋立面布置圖(單位：m)Fig.1 Elevation of a partially ground-anchored cable-stayed bridge with main span of 1 400 m

2 結構三維有限元模型

采用Midas/Civil有限元分析軟件，建立了如圖2所示的結構三維有限元模型，共計663 個節點和932 個單元，主梁、橋塔和橫梁采用空間梁單元模擬，斜拉索則采用空間桁架單元模擬，橋面主梁采用魚骨式計算模型，斜拉索與主梁之間連接采用剛臂單元模擬。結構模型約束信息為：主梁縱向漂浮，主梁與邊墩和輔助墩之間的橫橋向、豎向、繞縱軸三個方向自由度保持從屬關系，沿橋縱向位移、繞橫軸和豎軸轉動自由；主梁與橋塔下橫梁之間只有豎向約束，其他方向位移自由；橋塔底部和地錨處均按固結處理。

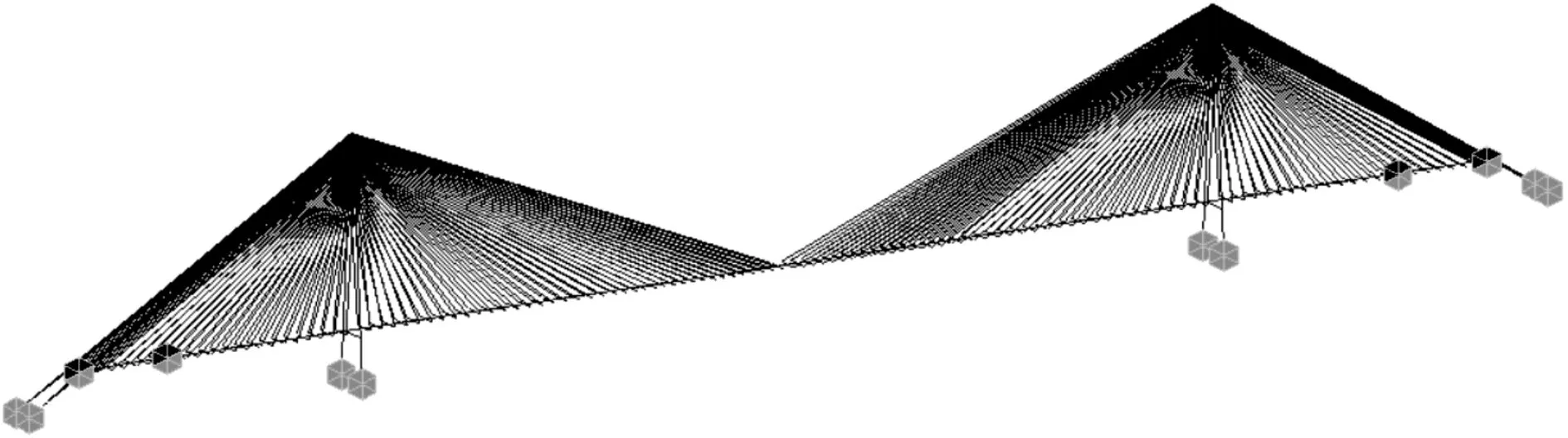
圖2 結構三維有限元模型Fig.2 3D structural finite element model

采用Midas/Civil有限元分析軟件的“未知荷載系數”功能和調索工具對該橋成橋狀態的斜拉索初始索力進行分析，在此基礎上考慮斜拉索初始索力、結構自重和二期恒載的共同作用，通過結構三維幾何非線性有限元分析計算出成橋狀態結構的幾何和內力狀態，以此作為后續結構動力特性和地震反應分析的基準態。

3 結構動力特性分析

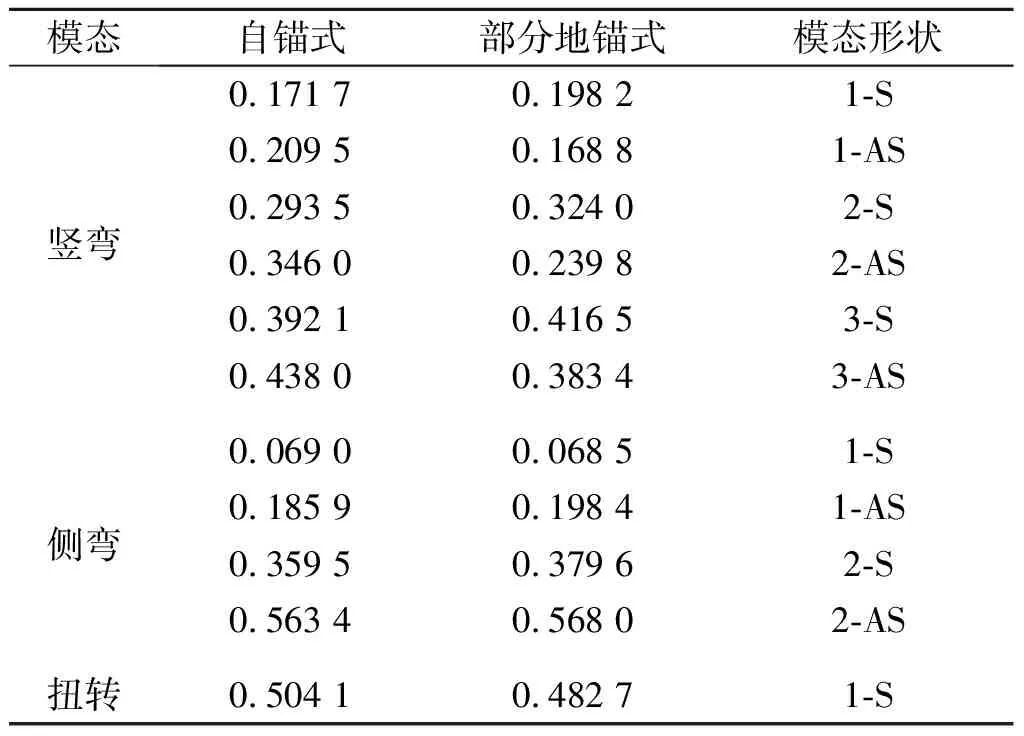
在計算成橋狀態基礎上，采用Midas/Civil有限元分析軟件的子空間迭代法分析了成橋狀態結構的前230 階振型，成橋狀態橋面主梁的相關主要振型如表1所示。

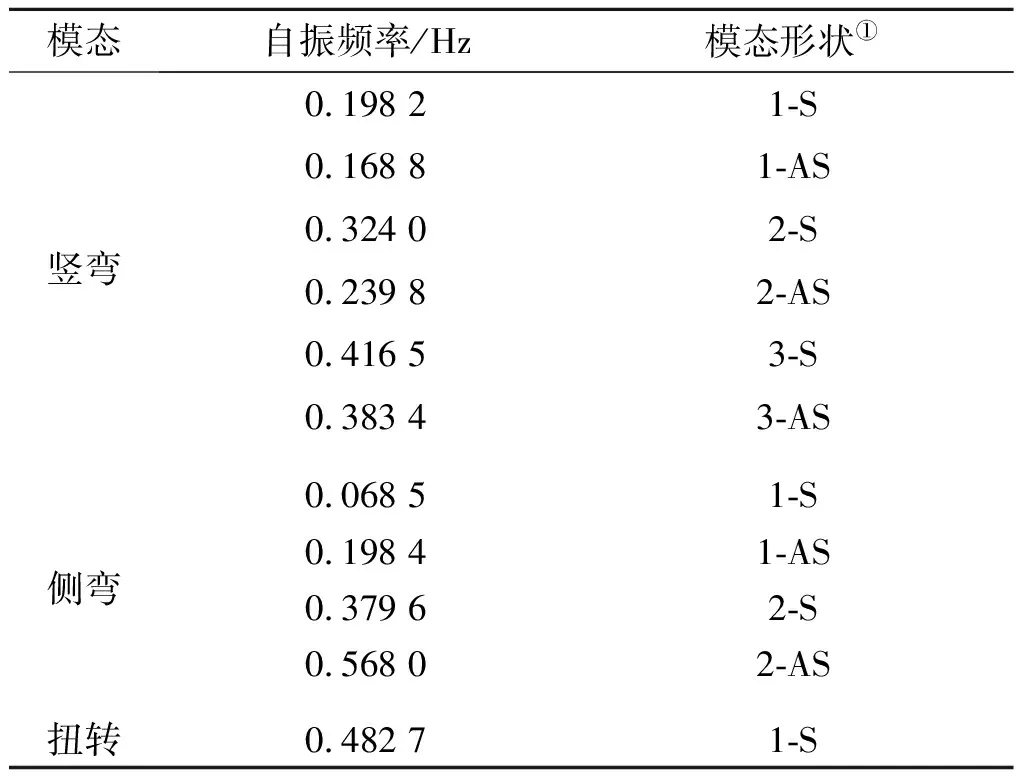
表1 橋面主梁振型及自振頻率Table 1 Natural frequencies and modes of the girder

① 數字表示振型序號；S表示對稱振型；AS表示反對稱振型。下同。

從表1結果可知：部分地錨式斜拉橋結構動力特性具有如下的特點：1) 結構基頻小，基本周期長(達到了14.6 s)，說明大跨度部分地錨式斜拉橋是一種柔性結構，結構的非線性效應將會比較顯著；2) 橋面主梁的側彎振型最早出現，緊接著是豎彎振型，而扭轉振型出現比較晚，一階豎彎和側彎振型的基頻比值達到2.893∶1，說明了大跨度部分地錨式斜拉橋的平面外剛度小，對風和地震等橫向動力作用將會非常敏感；3) 結構自振頻率密集分布，較窄的頻帶上分布著較多的振型，說明振型間的運動耦合強烈，因此大跨度部分地錨式斜拉橋的地震反應譜分析時其振型組合應采用CQC法。

4 大跨度部分地錨式斜拉橋結構地震反應分析

采用Midas/Civil有限元分析軟件，對設計方案橋進行E1和E2地震作用下的反應譜分析和時程分析，揭示其地震反應特點以及結構非線性的影響。

4.1 地震動輸入

設計方案橋為A類橋梁，橋址處抗震設防烈度為7 度；水平向設計基本地震動加速度峰值為0.10 g；場地類型為Ⅲ類，場地土特征周期為0.55 s；結構阻尼比為3%。根據《公路橋梁抗震細則》(JTG/T B02-01—2008)[15]確定分析采用的地震動反應譜，E1和E2地震作用的水平設計加速度反應譜如圖3所示，豎向地震動加速度反應譜取為相應水平設計加速度反應譜的1/2。

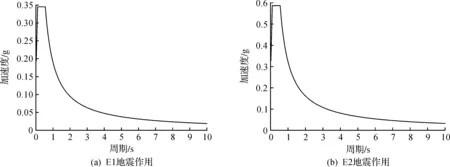
圖3 水平設計加速度反應譜Fig.3 Horizontal design acceleration spectrum

以上述規范反應譜為目標，采用三角級數迭加法擬合水平和豎向地震動加速度時程曲線，作為后續時程分析的地震動輸入。限于篇幅，圖4僅給出E1和E2地震動作用下各一條人工水平地震動加速度時程曲線及其反應譜與目標譜的比較。

圖4 人工擬合的水平震動加速度時程及其反應譜與目標譜的比較Fig.4 Comparison of the artificial horizontal seismic time histories and response spectrums with target spectrums

4.2 地震反應譜分析

基于MIDAS/Civil有限元分析軟件，在E1和E2地震作用下，采用多振型地震反應譜分析方法，考慮結構前230 階振型參與，對該設計方案橋分別進行縱向、橫向和豎向地震作用的結構地震反應分析，各振型的地震反應采用CQC方法組合。限于篇幅，在此僅給出橋塔和主梁的地震反應峰值，如表2所示。

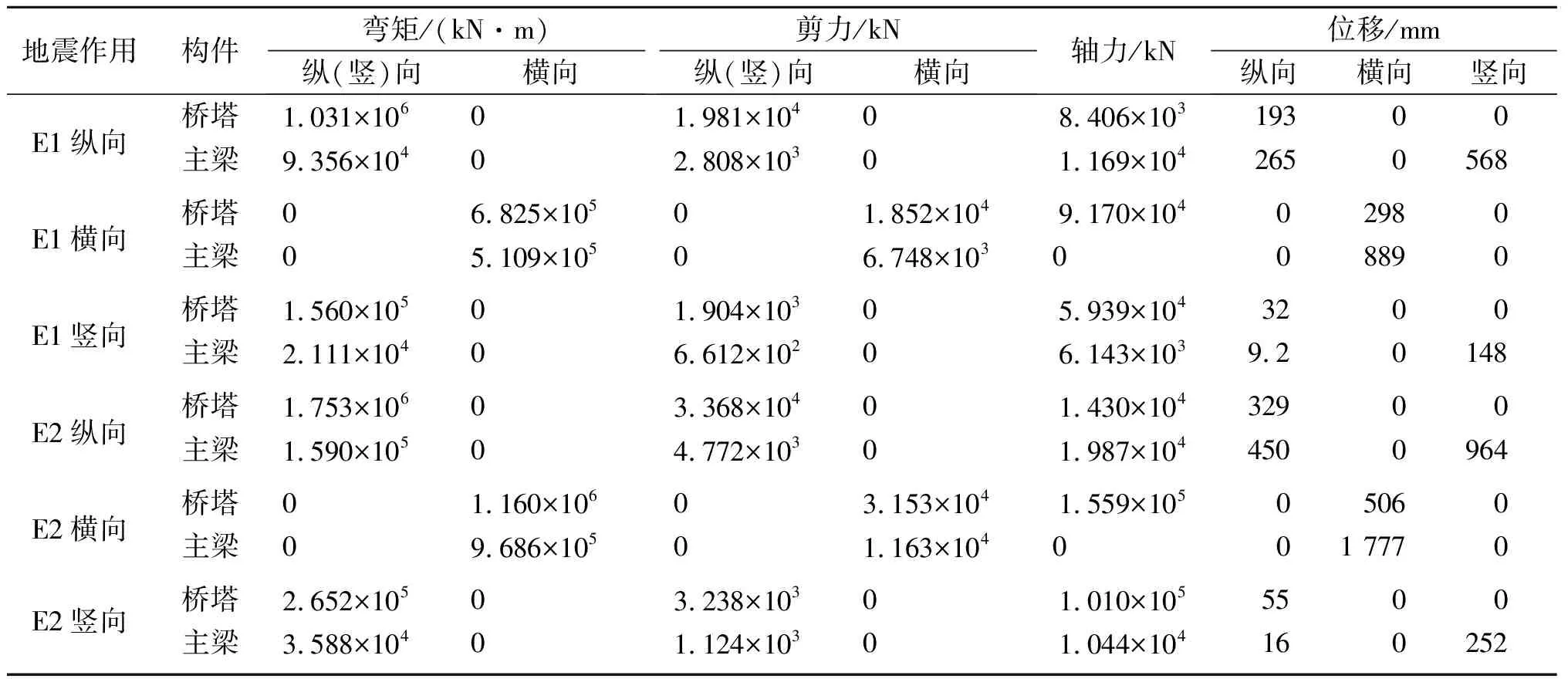
表2 結構地震反應峰值Table 2 Structural seismic response peak values

注：縱向和豎向地震作用下橋塔的彎矩和剪力均為縱橋向，主梁的彎矩和剪力則為豎向。下同。

由于重要性系數Ci的取值不同，E2地震作用的加速度反應譜最大值是E1地震作用的1.7倍，表3的E2各向地震作用下的結構內力和位移峰值約為表2的E1地震作用下相應反應峰值的1.7倍，說明了分析結果的可靠性。結合結構的地震反應包絡圖以及對表2，3的結構地震反應峰值進行綜合分析，超大跨度部分地錨式斜拉橋的地震反應具有以下特點：

1) 縱向地震作用下，橋塔順橋向振動，主梁則表現為順橋向和豎向耦合振動。橋塔塔頂處的縱向位移最大，并在塔底截面產生最大縱橋向彎矩、剪力和軸力；主梁沿橋軸向的縱向位移基本一致，并在中跨跨中附近產生最大豎向位移。主梁的最大豎向彎矩和剪力均出現在邊跨輔助墩處，其次為中跨跨中處。與主梁相比，縱向地震作用下橋塔受力更加顯著，并應特別重視塔底截面的抗震設計。

2) 橫向地震作用下，橋塔和主梁同時產生橫橋向振動。橋塔最大位移發生在橋塔上橫梁附近，最大橫向彎矩出現在塔梁連接處，最大橫向剪力和軸力則出現在塔底。主梁最大橫向位移出現在中跨跨中；最大橫向彎矩發生在塔梁連接處，中跨跨中橫向彎矩次之；最大橫向剪力發生在邊跨輔助墩附近，塔梁連接處次之。與縱向地震作用相比，橋塔和主梁的橫向地震反應更為顯著，橫向地震作用對結構受力更為不利，同時應特別重視塔梁交接處橋塔塔柱和主梁截面的抗震設計。

3) 豎向地震作用下，橋塔和主梁的振動形式與縱向地震作用基本相同。橋塔最大縱向位移出現在塔頂處，最大縱向彎矩、剪力和軸力都出現在塔底；主梁最大豎向位移出現在中跨跨中；最大豎向彎矩出現在輔助墩附近，中跨跨中次之；最大剪力也出現在輔助墩附近，最大軸力則出現在跨中。

4) 縱向和橫向地震作用下結構的地震反應均顯著大于豎向地震作用，因此應重視水平地震作用下超大跨度部分地錨式斜拉橋的抗震性能。同時，在縱向、橫向和豎向地震綜合作用下，橋塔的塔底和塔梁交接處、主梁的塔梁交接處和邊跨輔助墩處的地震反應均非常大，應特別重視這些截面的抗震設計。

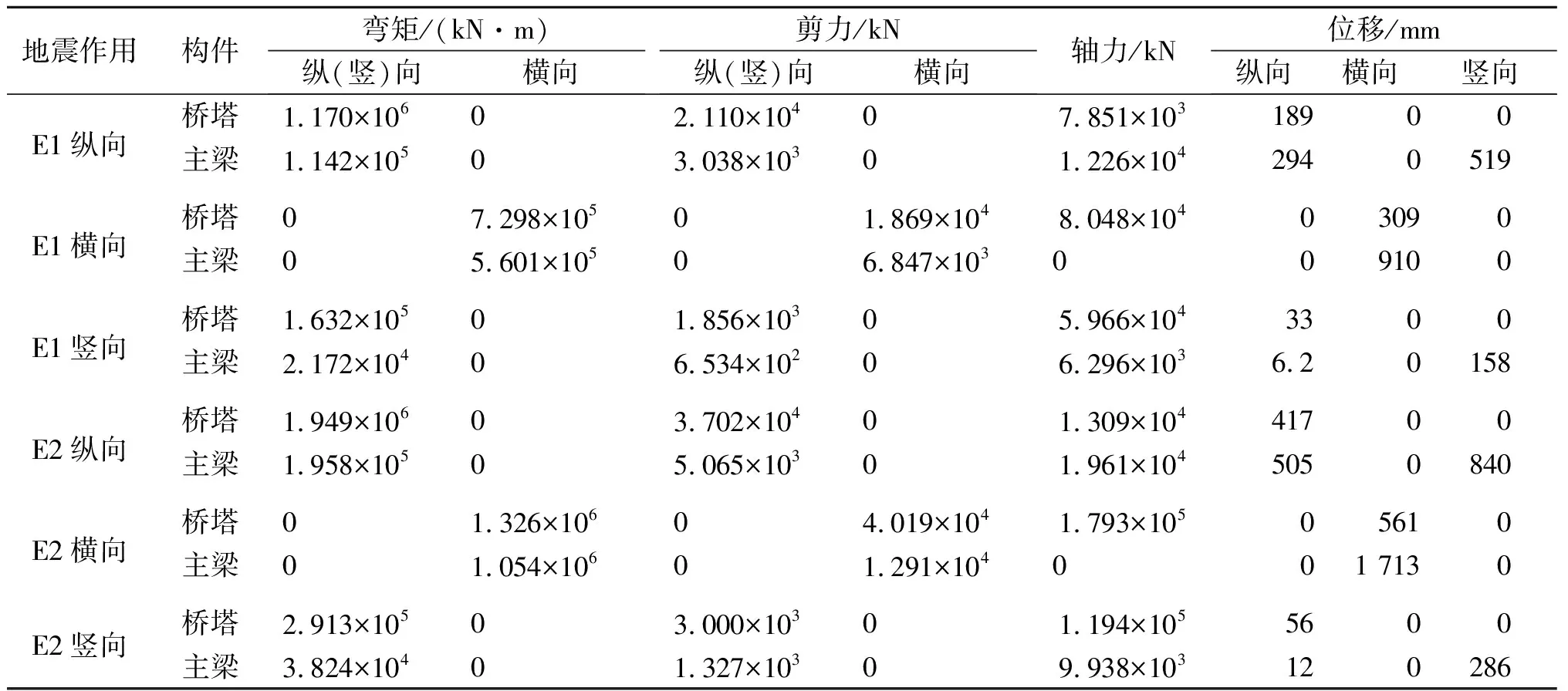
表3 結構地震時程反應峰值Table 3 Structural time-history seismic response peak values

4.3 地震反應時程分析

從前述的結構動力特性分析可知超大跨度部分地錨式斜拉橋是一種柔性結構，結構的幾何非線性效應將比較顯著。為了揭示結構幾何非線性對超大跨度部分地錨式斜拉橋地震反應的影響，采用如圖4的人工地震動時程曲線，對該橋進行E1和E2地震作用的縱向、橫向和豎向地震動輸入的非線性時程分析。分析時，每個方向均分別采用3條人工地震動時程曲線輸入進行分析，最后提取3組地震動計算結果的最大值列于表3。

與反應譜分析結果相比較發現，時程分析得到的主梁和橋塔的位移和內力峰值和出現位置基本相同，結構的地震反應特點一致。

4.4 反應譜分析與時程分析結果比較

為了揭示結構幾何非線性對大跨度部分地錨式斜拉橋地震反應的影響，在此將上述的反應譜和時程分析結果進行比較。規范指出：若同時考慮順橋向、橫橋向和豎向地震作用時，可分別單獨計算各方向地震作用產生的最大效應，總的最大地震作用效應取為各方向最大地震效應平方和的平方根[14]。為使分析結果比較更直觀，在此采用規范組合值進行比較，E1和E2地震作用下結構地震反應譜與時程分析結果比較如表4所示。

表4 結構地震反應譜與時程分析結果比較Table 4 Comparison of the results obtained by response spectrum and time-history analysis

從表4結果比較可以看出：E1和E2地震作用下，除了主塔軸力和主梁的豎向位移外，其余內力和位移的峰值結果均為時程分析大于反應譜分析，且E2地震作用下兩者的差異顯著大于E1地震作用情況。究其原因主要是時程分析考慮結構的幾何非線性效應，結構的整體剛度降低，使其地震反應明顯增大。因此，在進行大跨度尤其是超大跨度部分地錨式斜拉橋地震反應分析時，建議采用非線性時程分析方法以準確評估結構的抗震性能。

5 與相同主跨全自錨斜拉橋地震反應的比較

5.1 全自錨式斜拉橋方案簡介

以蘇通大橋為原型，擬定了如圖5的全自錨式斜拉橋方案，采用全漂浮體系，橋跨布置為(636+1 400+636) m，邊主跨徑比為0.454，兩側邊跨內距離邊墩156 m和336 m處各設置1 個輔助墩。主梁和橋塔結構形式與前述部分地錨式斜拉橋設計方案一致，斜拉索采用空間傾斜扇形雙索面布置，共計304 根(38×4×2)。

圖5 主跨1 400 m全自錨式斜拉橋立面布置圖(單位：m)Fig.5 Elevation of a fully self-anchored cable-stayed bridge with main span of 1 400 m

5.2 結構動力特性分析比較

采用Midas/Civil有限元分析軟件建立了全自錨式方案橋的三維有限元模型，如圖6所示，總計有741 個節點，1 014 個單元。采用子空間迭代法分析了全自錨式斜拉橋方案成橋狀態的前200階振型，與相同跨徑的部分地錨式斜拉橋成橋狀態自振頻率的比較見表5。

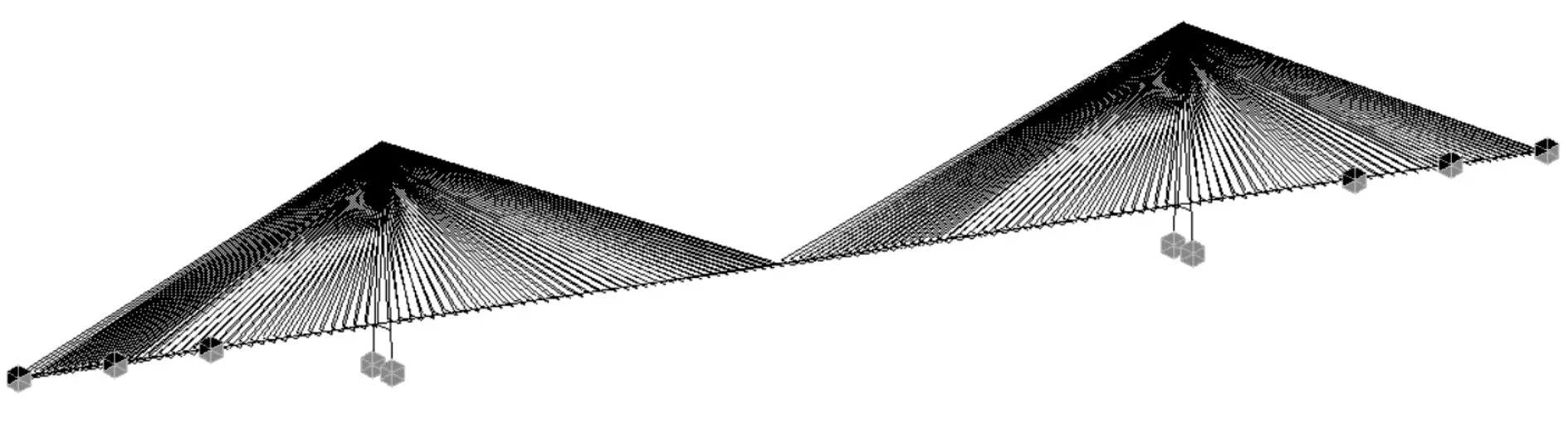
圖6 結構三維有限元模型Fig.6 3D structural finite element model

單位：Hz

由表5的結果比較發現：兩者的一階頻率都很小，基本周期均很長，說明兩者均屬于大跨柔性結構；部分地錨式斜拉橋的各階正對稱豎彎頻率和側彎頻率均大于全自錨式斜拉橋，扭轉基頻略小，說明邊跨部分斜拉索由自錨改為地錨后結構的豎向和側向剛度均得到提高，部分地錨式斜拉橋的結構剛度優于全自錨式斜拉橋。

5.3 結構地震反應分析比較

采用“4.1地震動輸入”所述的加速度反應譜和地震動加速度時程曲線，對自錨式斜拉橋方案進行E1和E2地震作用下的反應譜分析和時程分析，其計算結果與部分地錨式斜拉橋的比較如表6，7所示。

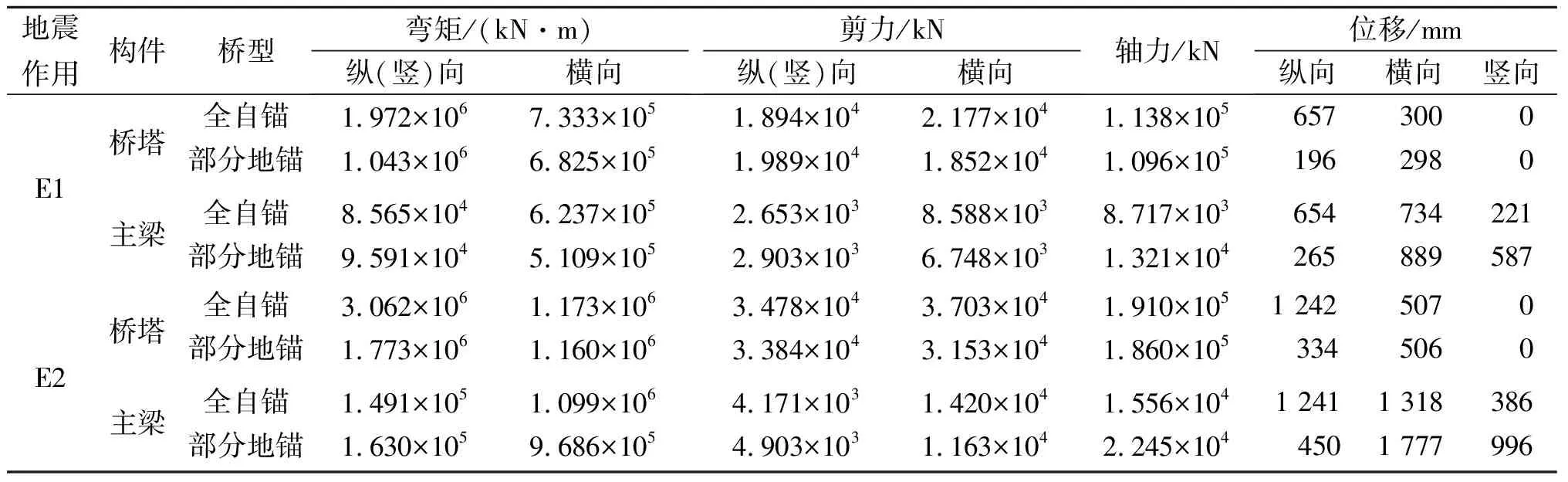
表6 不同橋型反應譜分析的地震反應峰值比較Table 6 Comparison of seismic response peak values of different bridges by response spectrum analysis

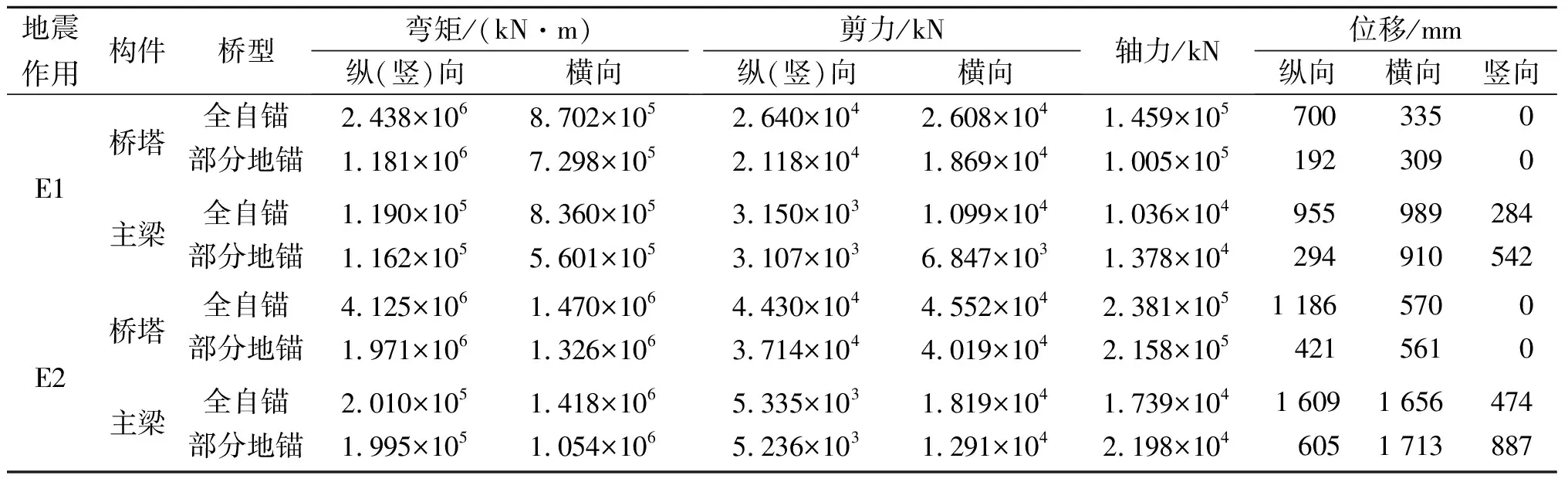
表7 不同橋型地震時程反應峰值比較Table 7 Comparison of seismic time-history response peak values of different bridges

在相同地震作用下，全自錨式斜拉橋主塔的內力和位移均顯著大于部分地錨式斜拉橋，特別是縱向彎矩和縱向位移，說明邊跨部分斜拉索采用地錨后，地錨式斜拉索對橋塔的縱橋向約束明顯增強，橋塔的抗震性能顯著提高。同樣地，在相同地震作用下，除橫向彎矩和橫向剪力外，部分地錨式斜拉橋主梁的各項內力均大于全自錨式斜拉橋；部分地錨式斜拉橋主梁縱向位移遠小于全自錨式斜拉橋，但其豎向和橫向位移則顯著大于全自錨式斜拉橋。由于部分地錨式斜拉橋邊跨長度(邊中跨比0.317)明顯小于全自錨式斜拉橋方案(邊中跨比0.454)，較短邊跨受到的橫向和豎向地震荷載對于抵消中跨的相應方向的地震荷載作用效果有限，導致中跨跨中產生更大的橫向和豎向位移及其相應的結構內力。因此，部分地錨式斜拉橋的邊跨不宜太小。總體上看，邊跨地錨索對控制橋塔的地震反應和主梁的縱向位移效果比較理想。同時，橋塔的地震內力均顯著大于主梁，是結構抗震設計的關鍵控制對象，因此采用部分地錨式斜拉橋方案將會更有利于改善結構的整體抗震性能。

6 結 論

結合主跨1 400 m的超大跨度部分地錨式斜拉橋設計方案，采用地震反應譜和時程分析方法，進行E1和E2水平和豎向地震作用下的結構地震反應分析，在此基礎上與相同主跨的全自錨式斜拉橋進行地震反應的對比分析，并得出了以下主要結論：

1) 超大跨度部分地錨式斜拉橋在縱向和橫向地震作用下的地震反應都顯著大于豎向地震作用，因此應重視水平地震作用下結構的抗震性能。在縱向、橫向和豎向地震綜合作用下，橋塔的地震內力顯著大于主梁，是結構抗震設計的關鍵構件，同時應特別重視橋塔的塔底和塔梁交接處、主梁的塔梁交接處和邊跨輔助墩處等截面的抗震設計。

2) 考慮結構的幾何非線性效應后，時程分析得到的結構地震位移和內力峰值均比反應譜分析結果大，特別是在E2地震作用下兩者相差較大。因此，超大跨度部分地錨式斜拉橋的地震反應分析宜采用非線性時程分析法。

3) 與相同跨度的全自錨式斜拉橋相比，邊跨部分斜拉索改為地錨后，結構剛度和自振頻率增大，橋塔的地震反應和主梁的縱向位移均顯著減小，改善了結構的整體抗震性能。因此，從抗震性能而言，超千米主跨斜拉橋更適宜采用部分地錨式結構形式。