數學思想方法在二次函數中的應用
莊梅芳
(福建省晉江市南灣中學 福建 晉江 362200)
1.分類討論思想在二次函數中的應用
分類討論思想是一種重要的數學思想,在解決二次函數問題時經常用到。許多二次函數問題,往往在相同的題設下,會產生幾種不同的結果,這就需要借助于分類討論思想按照同一標準,確定分類對象,把可能存在的一切情況都列舉出來,一一加以研究,然后進行歸納,合并,綜合得出結論。
例1,已知拋物線y=ax2+bx+c(a>0),它與x軸交于點A和B,與y軸交于點C,試求S△AoC+S△BoC
解:設A(x1,0),B(x2,0)則x1,x2就是二次方程ax2+bx+c=0的兩個實根。
而OA=|x1|,OB=|x2|, 又由x=0時,y=c得OC=|c|
已知a>0,下面就c的不同符號分別計算S△AoC+S△BOC的值
(1)當c=0時,顯然有S△AoC+S△B0C=0
(2)當c>0時,x1和x2同號
i)若x1和x2都為正數,則b<0,
ii)若x1和x2都為負數,則b>0
(3)當c<0時,x1和x2異號,不防設x1>0,x2<0,則
OC=|c|=-c
2.轉化思想在二次函數中的應用
轉化思想是一種最基本的數學思想,是解決二次函數問題不可忽視的方法。二次函數的問題一般都是綜合性很強的題目,如何把復雜的問題向簡單的問題轉化,是解題成敗的關鍵所在。轉化思想在二次函數中運用的思想一般是把生活、生產、科研中的實際問題通過建立數學模型轉化為數學問題;把幾何問題轉化為函數問題;把位置關系轉化為數量關系;把非常規問題轉化為常規問題,最終實現未知向已知的轉化,從而使問題得到解決。
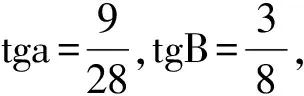
(1)若導彈運行軌道為一拋物線,求該拋物線的解析式;
(2)說明按(1)中軌道運行的導彈能否擊中目標C的理由。
解:(1)設導彈運行軌道的拋物線解析式為y=ax2+bx+c,由題意知,這條拋物線的頂點坐標為E(4,3)
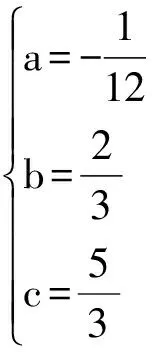
(2)設C點的坐標為(xo,yo),過C作CB⊥0X垂足為B,在Rt△OBC和Rt△ABC中,OA=1,
3.方程思想在二次函數中的應用
方程思想是一種廣泛應用的數學思想,是解決二次函數問題的一個有力工具。在二次函數問題中,或多或少存在著等量關系,我們經常把所研究的二次函數問題中的數量關系,轉化為方程或方程組等數學模型,通過解方程或方程組,實觀未知向已知的轉化。可見,方程思想方法,對解決二次函數問題,作用十分重大。如待定系數法求二次函數解析式,求解幾何圖形中的函數關系,求二次函數與其他圖形的交點問題等,都離不開方程思想。
例3已知二次函數y=x2+bx+a(b<0)的圖像與y軸交于點P(0,3),與x軸交于A、B兩點,且AB=2
(1)求bc的值,并寫出這個函數的解析式;
(2)過P點作x軸的平行線,求這條平行線被二次函數圖像所截得的線段的長;
(3)求△PAB的面積;
解:(1)∵P(0,3)在圖像上,將其坐標值代入y=x2+ bx+c(b 即得c=3設A(x1,0),B(x2,0),則x1、x2是方程x2+bx+3=0的根。 ∵AB=2,即|x1-x2| ∵b<0, ∴ b=-4 ∴所求的解析式為y=x2-4x+3 (2)設過P且平行于x軸的直線與圖像的另一交點為Q,則P、Q的坐標就是下面方程組的解: 數形結合思想是一種典型的數學思想,是研究二次函數問題離不開的思想方法。數學是以現實世界中的空間形式與數量關系為研究對象,即數學是研究數、形及其關系的一門科學。在建立直角坐標系后,平面上的點就可以用坐標來表示,進一步又可建立平面上曲線與方程間的聯系,這就使數與形結合起來,二次函數問題正是這種思想的充分體現,使數和形的結合達到了一個新的境地。在二次函數問題中,我們通過圖形形象直觀地表示出抽象的數量關系,即利用形來研究數,另一方面,通過數量計算準確地表示出圖形的性質即利用數來研究形。數形結合思想的運用,是驗證二次函數解題能力和創造性的有力根據。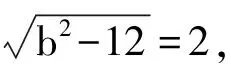

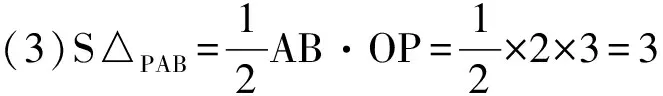
4.數形結合思想在二次函數中的應用

