有限平面波疊加模擬中低頻混響聲場的方法

朱衛紅，高 強，鄒元杰

（1. 北京空間飛行器總體設計部，北京 100094； 2. 中國航天科工防御技術研究院，北京 100039）

0 引言

在航天任務過程中，航天器能否經受住發射段嚴苛的力學環境考驗，是決定任務成敗的關鍵因素之一[1]。而噪聲環境是其中最為典型的一種動力學環境，可能造成機電設備、光學儀器、電子電路等的失效或性能下降，以及部分部組件（如天線、饋源等輕質薄璧結構）的結構性破壞。

噪聲載荷的分布頻段較寬（20 Hz～10 kHz）。航天工程中針對不同的頻段采用不同的分析方法進行聲振力學環境預示[2-3]：在低頻段采用結構有限元-聲學邊界元方法建模，即航天器結構采用有限元方法、航天器的內外聲場采用邊界元方法[4]；在中頻段采用有限元-統計能量分析方法建模，即對模態密度較低的結構、關鍵設備等采用有限元方法，對高模態密度結構和聲場采用統計能量分析法[5]；在高頻段主要采用統計能量分析方法建模[6]。不論采用哪種方法，都需要建立準確的噪聲載荷模型。

目前，通常采用擴散聲場（DAF）載荷方法建立噪聲載荷模型，假定噪聲空間為完全混響空間，基于直接場與擴散聲場的互易關系，將聲壓轉化為網格節點上的力譜，直接施加在結構上求解[7]。該方法能夠描述聲場載荷的空間相關性，但是只在其施加的區域內滿足，無法刻畫混響聲空間中由于結構存在導致的聲場不均勻性；另外該模型主要面向結構的承載，無法考慮結構本身的聲輻射、散射特征，因此需要結合半無限聲場系統來模擬結構的聲輻射等特征[8]。而采用平面波疊加模擬噪聲載荷，能夠刻畫整個聲空間的載荷空間相關性。這種噪聲載荷模型結合有限元-邊界元模型，可充分刻畫聲散射、輻射和聲載荷的不均勻性，但與DAF 不同的是只能施加在聲學邊界元模型中。高強等[9]研究了平面波疊加對聲場載荷的空間相關性影響，證明該方法能夠準確描述載荷的空間特征，但是如何基于該方法建立混響載荷模型尚未得到解決。

本文提出采用基于隨機相位的平面波疊加方法建立中低頻混響載荷，結合傳統結構有限元-聲學邊界元模型建模方法進行聲振響應預示。文中對基于平面波疊加的混響載荷建模方法的理論、空間特征及平面波數目的確定方法進行詳細的研究，并結合實際工程算例驗證該方法的可行性與有效性，可為后續的航天工程應用提供支撐。

1 基于平面波疊加的混響載荷建模

1.1 多列平面波疊加的聲能密度

混響聲場是一種理想的聲場，在聲場各個位置處，聲能量向各個方向的傳播概率相同，平均聲能密度處處相同。設在聲場中有一足夠小的體積元，聲壓為p，空氣密度為ρ0，則其聲能密度為

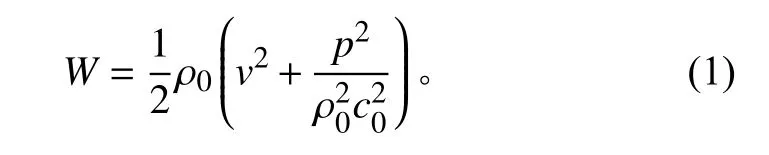
式中：v為體積元速度；c0為空氣中的聲速。

定義平面波的聲壓[10]為

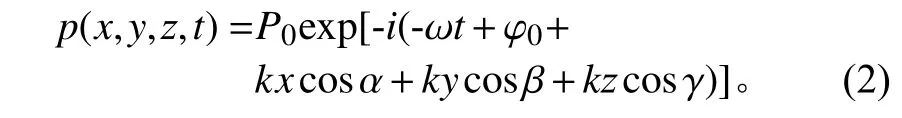
式中：x、y、z為空間位置坐標；t為傳播時間；P0為平面波聲壓幅值；ω為平面波的角頻率；φ0為初始相位；k為波數；α、β、γ為平面波傳播的方向角。

對固定空間位置的平面波，在1 個振動周期T內求取其聲能密度的平均值，有

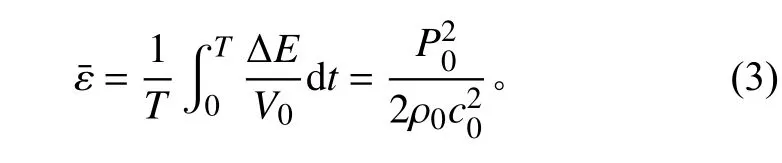
式中：T=2π/ω；ΔE為平面波的能量；V0為聲場的體積。可以看出，平面波的平均聲能密度僅與其聲壓幅值有關，而與相位和位置無關。

對于具有相同波長的2 列平面波，在該位置處的聲壓為

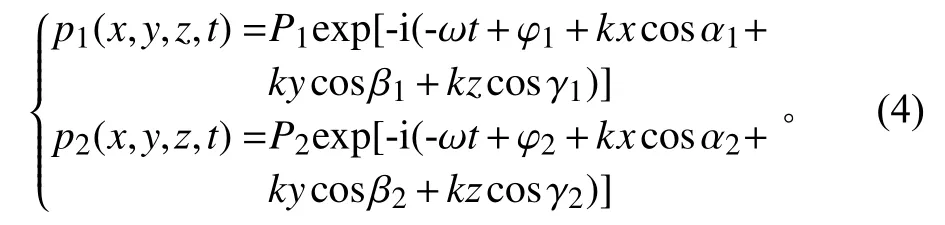
在1 個周期內對聲能密度進行平均，有

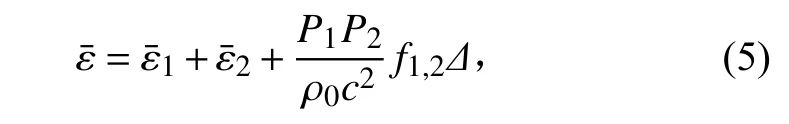
式中：

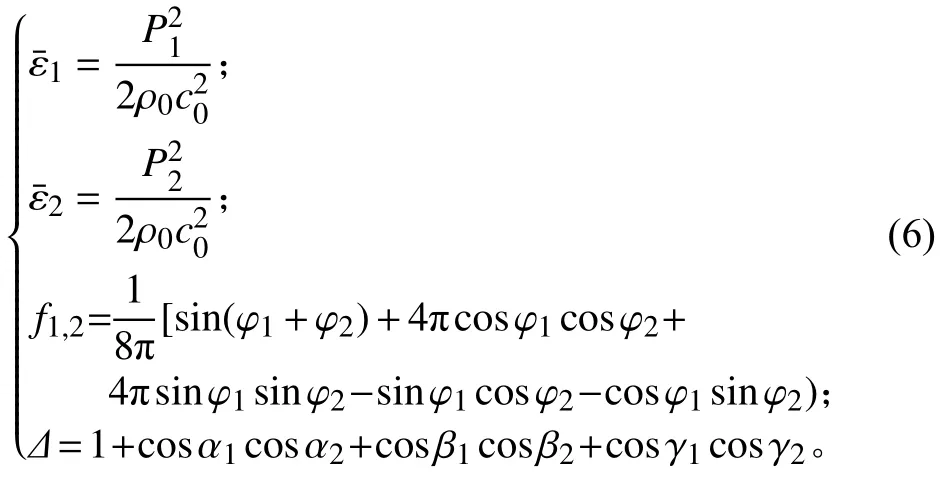
如果相位 φ1和 φ2平均分布在區間[0, 2π]內，則相位相干函數的均值為0，即

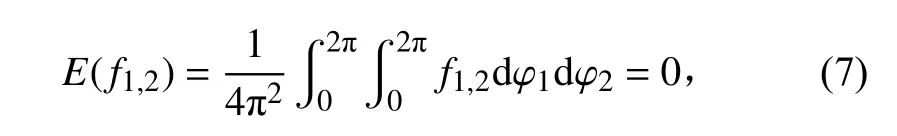
則

因此，對于具有隨機相位的2 個平面波之總成，其1 個周期內的平均聲能密度等于其中每列平面波平均聲能密度的線性疊加。同理可以推得，對于n個平面波之總成，其1 個周期內的平均聲能密度為

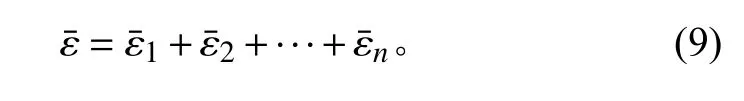
1.2 基于混響載荷聲壓的平面波分布設計

1.1 節的分析表明，在各個平面波相位隨機的情況下，平面波的聲能密度滿足線性疊加原理。

假設將整個聲空間建立在球坐標系中，將聲空間球面按照經度和緯度進行切分，將緯度分為m層，則每層之間的角間隔為Δθ=π/m，θi=Δθ/2+(i-1)Δθ, (i=1, ···,m)；將經度分為n層，每層之間的角間隔為Δψ=2π/n，ψj=Δψ/2+(j-1)Δψ, (j=1, ···,n)。如圖1 所示，假定球坐標的中心為物理坐標原點，令緯度為θi、經度為ψj位置的聲壓幅值為Pij，其空間矢量方向為

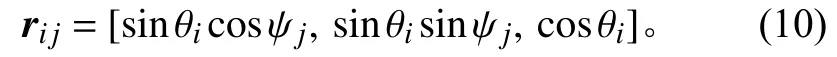
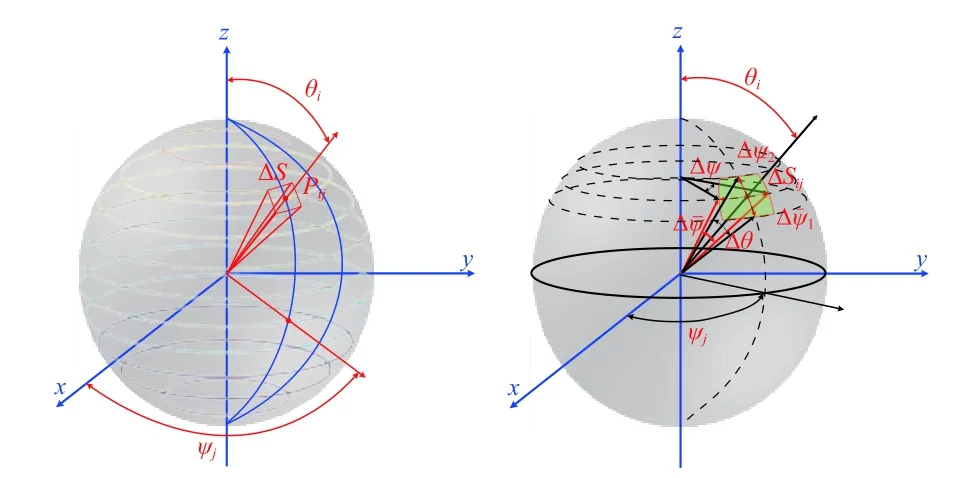
圖 1 平面波位置及其有效輻射面積示意Fig. 1 Locations and effective action area of plane waves

平面波將球體分為m×n份，假設平面波Pij作用在球面上的面積為Sij，面積元在緯度方向上的球面寬度為Δθ。因此，平面波Pij在球面上的作用面積近似為

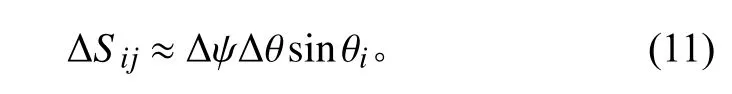
為了保證混響場在球面上的能量均勻分布，須滿足：

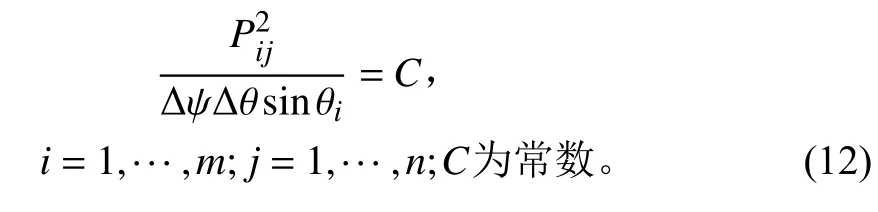
對于具有均勻分布隨機相位的平面波，其平均聲能滿足線性疊加關系，即

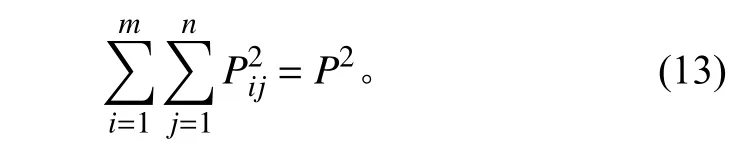
因此，每個平面波的聲壓幅值可以表示為

例如，取n=m=2，計算得到θi=[45°, 135°]，ψj=[90°, 270°]，P2=1，則不難計算得到：

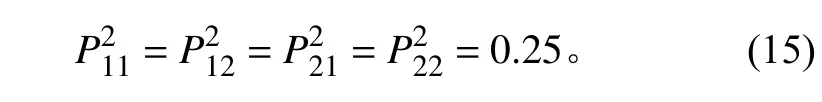
圖2 為平面波在整個球面上的聲壓貢獻量分布，可以看出，采用經緯度劃分的方式，球面的兩極位置聲壓幅值非常小，赤道附近聲壓幅值最大。這是由于在不同的位置，平面波之間的間距和有效面積不同導致的；如果采用球面等分方式確定平面波位置，那么球面上的聲壓將會平均分布。

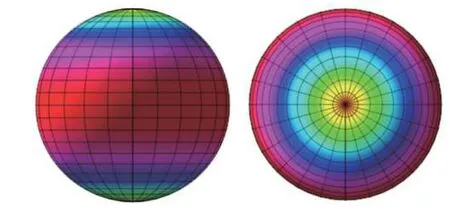
圖 2 平面波在球面上的聲壓幅值分布Fig. 2 Acoustic pressure distribution on the spherical surface

2 基于平面波疊加的混響場空間特征分析

根據式(10)，可計算得到波數在3 個軸方向上的分量，對于平面波Pij，有：

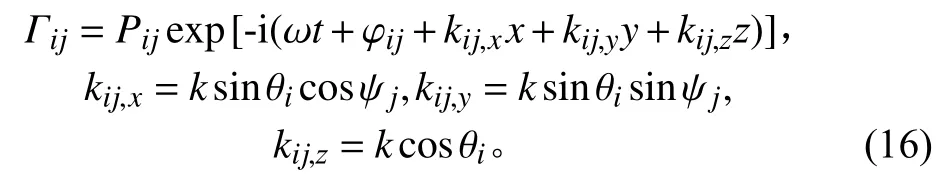
假設在結構表面有l個節點，則每個節點處的聲壓值為

聲壓的互譜功率譜密度為

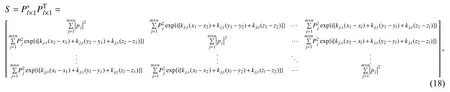
其中非對角元素代表的是空間任意兩點之間的互譜密度。設節點u和v之間的矢量為r，定義其與平面波方向的夾角為βj，則互譜功率譜密度可簡寫為

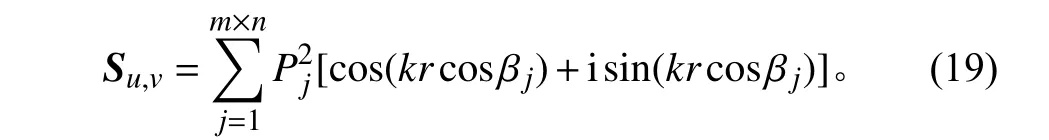
將式(14)代入式(19)，則有：

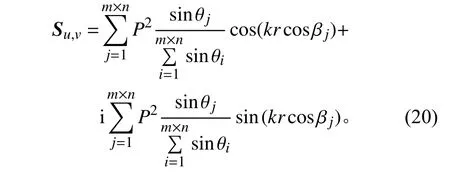
設矢量r的方向角為[ε,?]，則有：

當m→∞,n→∞時，Δθ→0, Δψ→0，則求和可近似用積分表示，

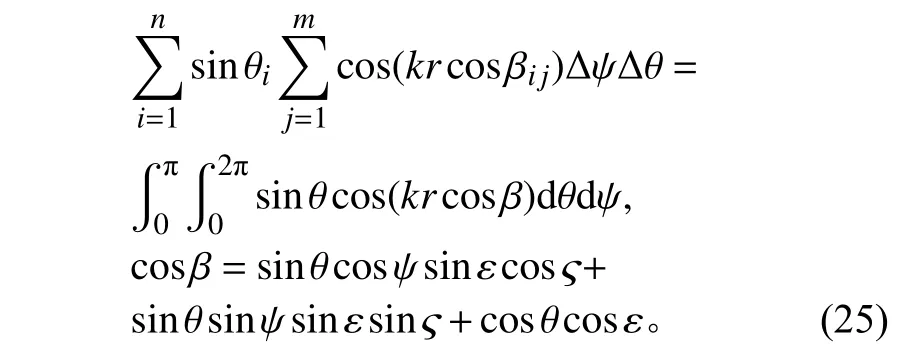
因此，可將式(20)改寫為

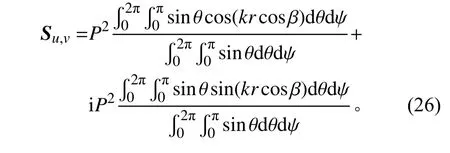
3 平面波疊加的混響聲場空間特征驗證與數目確定方法

3.1 平面波疊混響載荷的空間相關性分析

公式(26)無法直接進行積分計算，需要作一些數學處理。在此考慮取系統坐標系的z軸與距離矢量r重合，矢量r與矢量k之間的夾角為θ，因此有cosβ=cosθ，則式(26)中的各項積分可寫為：

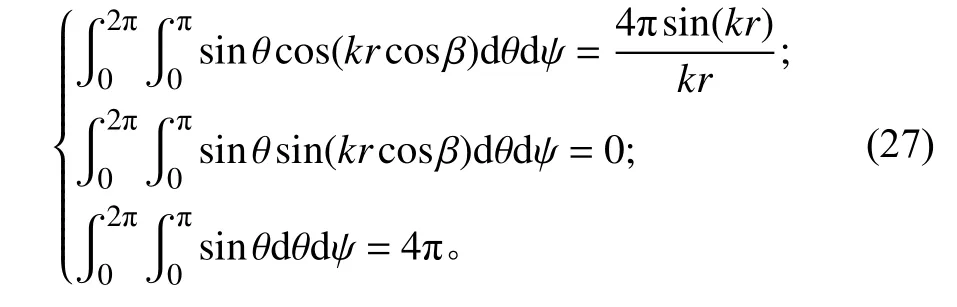
則有

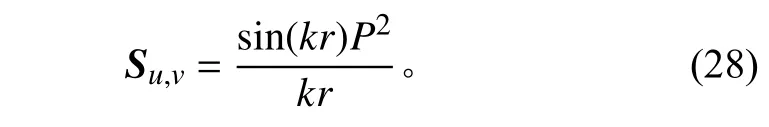
根據空間相關性系數的定義

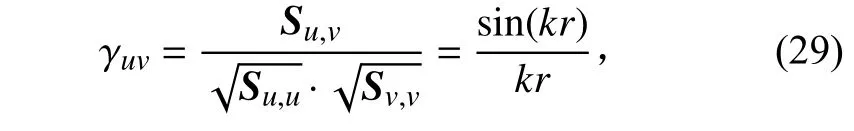
上述結論與理論解[11]完全一致。

對于任意空間矢量r，無法直接獲得解析解，這里采用數值解法驗證對于任意的空間兩點均滿足理論相干系數。圖3 為空間矢量r=[172.35°,347.35°]無限多平面波疊加模擬的空間相關性與理論相關性的對比結果，可以看出，不論是隨著波數k的變化還是隨著距離r的變化，無限多平面波疊加模擬的空間相關性與理論相關性的誤差均小于10-4dB。

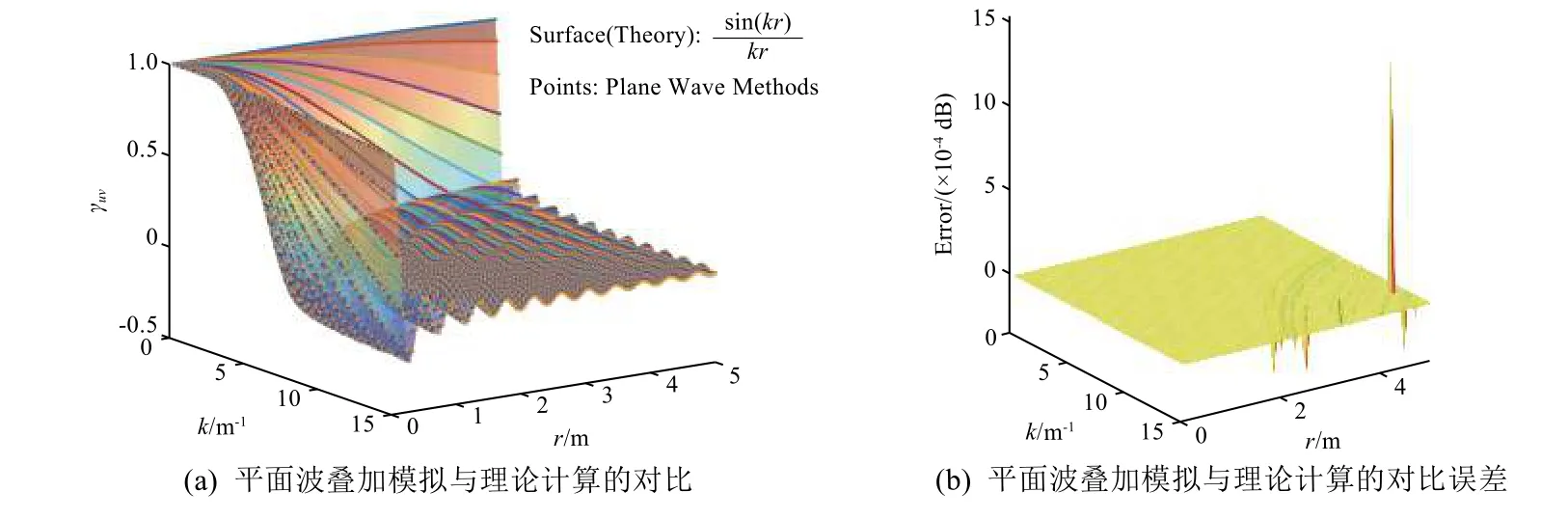
圖 3 任意空間矢量r 的空間相關性（無限多平面波疊加模擬與理論值的對比）Fig. 3 Spatial correlation coefficient of an arbitrary vector

理論上，當整個空間中分布無限平面波時，其疊加結果滿足理論空間相關性，而幅值是通過對已知混響聲壓進行分解得到，因此其疊加聲壓與實際混響聲壓也是相等的。然而在實際的工程應用過程中，混響場只能采用有限的平面波疊加進行近似，因此其空間相關性會存在一定的建模誤差，下面對誤差進行分析。

圖4 為針對固定的空間矢量r，當平面波數目n分別為2、8、16、32 時，通過Monte Carlo 仿真（仿真次數250）得到的平面波疊加的聲場空間相關性隨著(kr)的變化。可以看出，平面波數目越多，模型與理論解越吻合，n=32 時基本與理論解一致。因此，采用有限數目的平面波疊加模擬混響場時，模型的空間相關性與平面波數目n、空間點位置矢量r相關；但是隨著平面波數目的增加，兩者的影響越來越小。

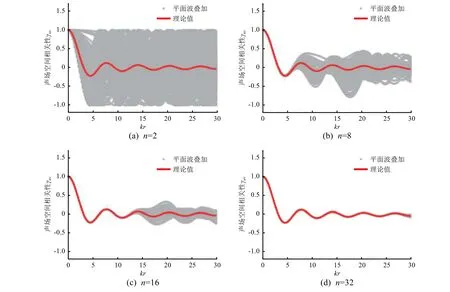
圖 4 空間相關性與平面波數目和位置矢量的關系Fig. 4 The spatial correlation coefficient against the number and the location vectors of plane waves

3.2 平面波數目的確定方法

一般而言，采用聲學邊界元和有限元建模用于低中頻的聲振耦合分析，而平面波的數目與分析頻率的上限和航天器結構的特征尺寸（最大包絡尺寸）密切相關。以分析頻率上限和結構最大包絡尺寸為參數，以空間理論相關性為目標函數，以經度與緯度的平面波數目（二者相等）為自變量，確定使得目標函數滿足給定誤差。容差函數是具有多個零點的振蕩函數，在零點處無法定義相對誤差；考慮到空間相關性最大值為1，并隨著分析頻率與空間距離的增加逼近于0，因此取絕對誤差。這里僅給出絕對誤差為0.01 的結果：

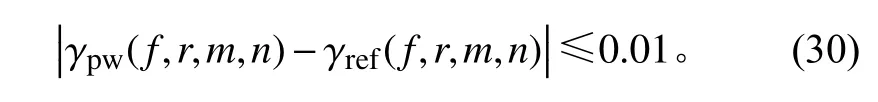
圖5 為容差為0.01 時，平面波數目n與最大包絡尺寸r和分析頻率上限f的關系。為了便于工程應用，采用二次曲面進行擬合，n、r、f滿足如下關系：

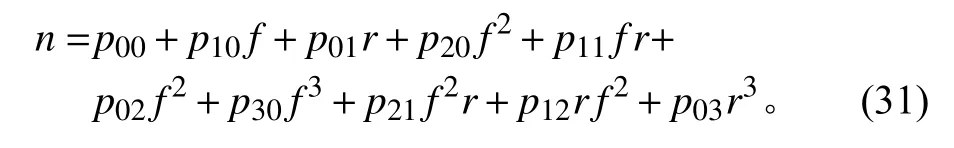
其中：

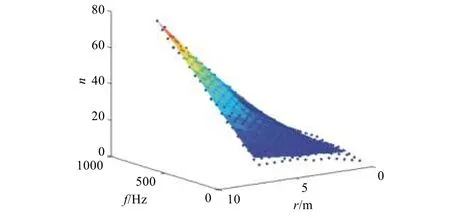
圖 5 平面波數目n 與最大包絡尺寸r 和分析頻率上限f 的關系（容差0.01 時）Fig. 5 The number of plane waves vs. the max envelope size and the top analyzing frequency

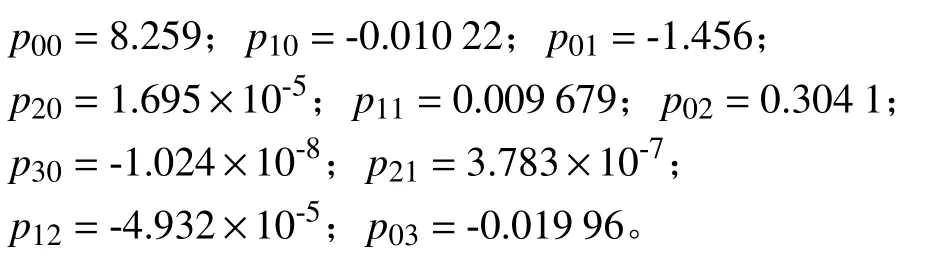
根據公式(31)確定的平面波數目疊加后，模型的空間相關性基本與理論解吻合，參見圖6。

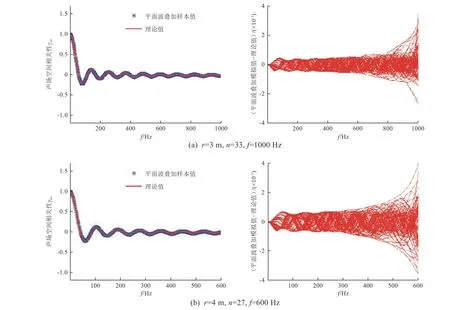
圖 6 根據擬合公式確定的平面波數目疊加后模型的空間相關性Fig. 6 The spatial correlation of the model by superimposed plane waves determined by the fitting equation

本文提出的方法偏于保守，而且給出的經驗公式假定經度方向和緯度方向的平面波數目相同。在實際工程應用中，需要通過多次不同的平面波數目仿真進行對比分析，最終綜合精度和運算的要求，確定合理的平面波數目。

4 工程應用與驗證

下文將依據本文提出的混響載荷建模方法，結合混合有限元-邊界元建模方法，開展混響載荷的聲學特征與航天工程應用案例分析，驗證方法的有效性。

4.1 多列平面波疊加模擬混響聲場

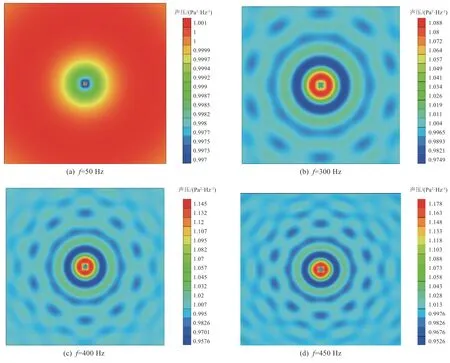
圖 7 平面波疊加模擬混響聲場的聲壓分布Fig. 7 Pressure distribution of reveberant sound field overlayed by plane waves

針對聲場中的方形障礙物，采用多列平面波疊加模擬混響載荷分析障礙物對聲場的散射效應。圖7 為多列平面波疊加后不同頻率下整個聲空間的聲壓分布。由圖可以看出：整個聲空間的聲壓與期望聲壓（1 Pa2/Hz）基本一致，聲壓分布均勻；在障礙物或者結構表面仍有明顯的硬邊界效應，不同的頻率下硬邊界效應的區域分布大不相同，因此如果直接在結構表面施加等效的聲壓載荷，可能無法準確描述該特征。

4.2 低頻混響載荷的遮擋效應模擬

采用平面波疊加模擬混響場可刻畫復雜結構在混響聲場中由于其幾何構型導致的遮擋效應，如果直接在結構表面施加聲載荷則無法刻畫之。以某結構尺寸為0.5 m×0.5 m×4 m 的復雜構型結構（參見圖8）為例，研究在混響載荷（多列平面波疊加模擬）下的聲場聲壓分布情況。圖9 所示為在不同頻率下結構遮擋效應引起的聲壓分布：由于構型原因，在不同位置不同頻率下聲壓的分布差異較大，尤其是在低頻下，窄小聲腔結構引起的聲壓放大達到15 dB。這可能是低頻結構由于聲載荷導致破壞的原因之一。

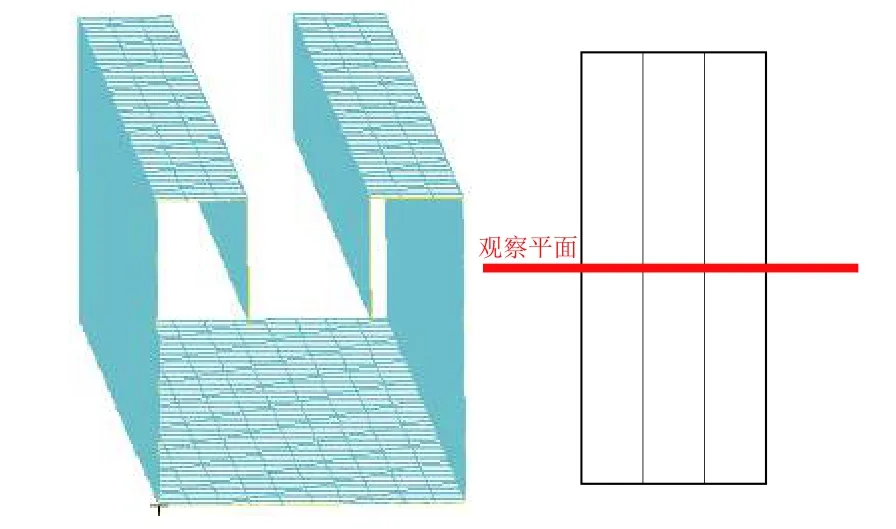
圖 8 遮擋效應分析模型Fig. 8 Illustration of masking effect

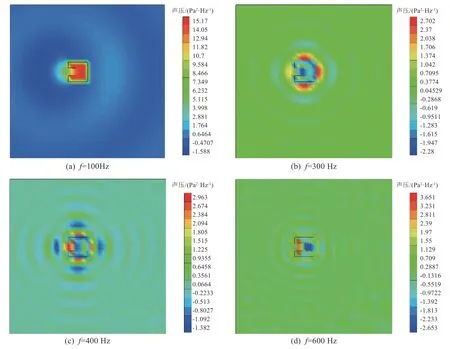
圖 9 不同頻率下結構遮擋效應引起的的聲壓分布Fig. 9 Pressure distribution change of different frequencies due to masking effect

4.3 太陽電池陣聲振響應分析與驗證

采用某平臺的太陽電池陣模型進行噪聲試驗，每塊電池陣由內外2 塊板構成。試驗時，南北太陽電池陣同時安裝在模擬墻上，如圖10 所示。根據試驗要求在太陽電池陣外側板布置約10 個測點，太陽電池陣的聲振響應以面外響應為主，因此主要考察面外響應，測點布置如圖11 所示。仿真載荷采用試驗給定條件確定：試驗條件為遠場聲壓，因此邊界元載荷定義時采用遠場聲壓；試驗條件是在倍頻程下給定的，因此需要通過計算轉換為4 Hz 等帶寬的載荷；為了模擬測量噪聲，在載荷中引入噪聲。

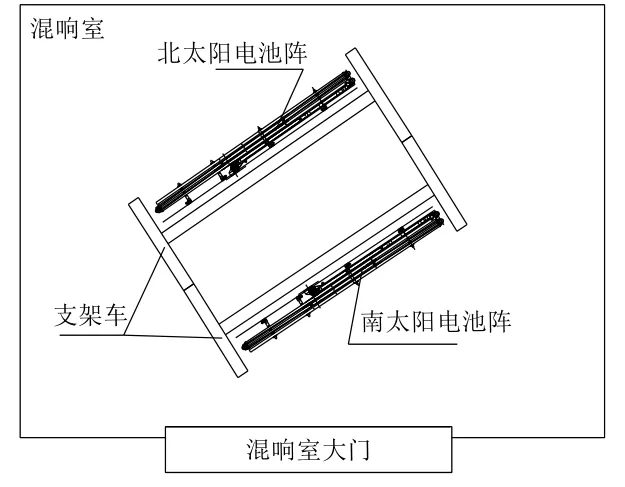
圖 10 太陽電池陣試驗狀態Fig. 10 Acoustic test of solar panels

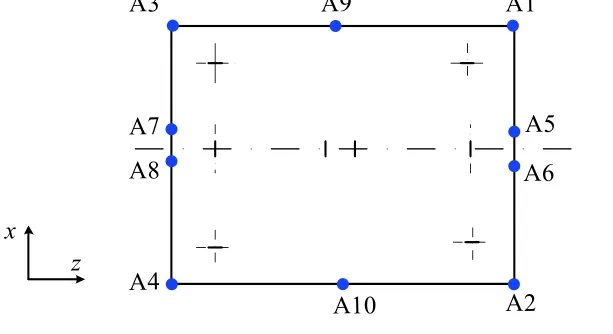
圖 11 太陽電池陣測點布置Fig. 11 Locations of sensors on the solar panel

通過對仿真分析結果對比觀測發現，測點的位置攝動對預示結果的影響較大，因此在測點附近選取多個測點測量結果與試驗結果進行對比。太陽電池陣上10 個測點的加速度響應結果如圖12 所示。可以看出：基于本文提出的混響載荷建模方法能夠準確描述太陽電池陣聲振試驗所經受的聲載荷，預示結果與試驗結果基本吻合。為進一步分析測點位置精度對仿真結果的影響，圖13 給出了測點8 附近15 個不同位置的響應預示結果與試驗值的總方均根誤差，發現最大誤差大約為4 dB，南板與北板的誤差分布基本一致，仿真模型與實際結構的測點位置存在的偏差會對仿真結果的準確性造成一定的影響。總體而言，在實際工程應用中可以通過改善模型精度、聲載荷譜的準確程度以及測點的位置精度來不同程度地提高預示結果的準確度。

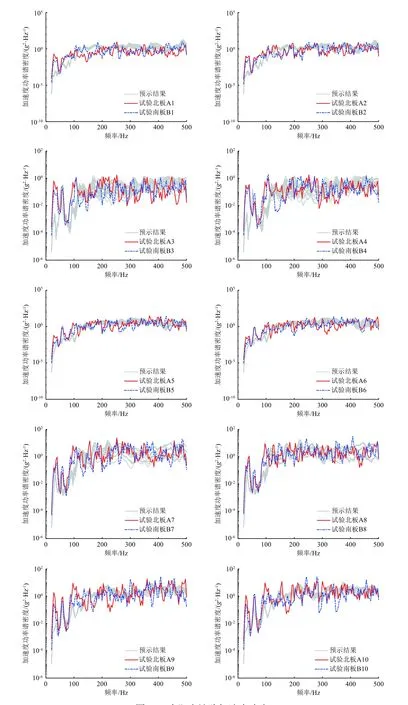
圖 12 太陽電池陣加速度響應Fig. 12 Acceleration responses of the solar panels

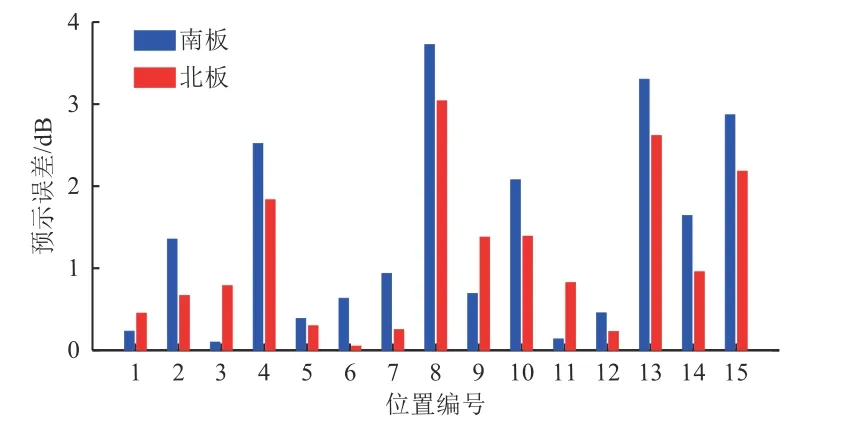
圖 13 測點8 附近不同位置的聲場響應預示誤差Fig. 13 Influence of sensor location on the RMS vibroacoustic response of the sound field

5 結束語

本文提出在平面波中引入隨機相位，通過平面波疊加模擬航天器經受的混響聲場載荷；當平面波的數目足夠多時，則整個聲空間的分布特征滿足理論空間相關性，能夠較為準確地模擬低頻段的聲空間模型。

數值算例分析表明：1）采用隨機相位的平面波疊加的混響載荷建模方法，整個聲空間的聲壓與期望聲壓基本一致。與傳統分析中將硬邊界效應定義為剛性邊界放大3 dB 不同，基于本文方法能夠明顯觀察到結構周圍的硬邊界特征，得到的硬邊界效應是隨著頻率變化的，其規律有待于進一步深入研究。2）本文提出的建模方法能夠描述復雜結構幾何形狀引起的遮擋效應，因此能夠改善中低頻聲振預示的精度。

實際工程應用案例表明：試驗結果與采用本文方法建立混響載荷模型進行聲振預示的分析結果基本吻合，驗證了本文方法的有效性。但傳感器的位置誤差會對分析結果有一定的影響，應予以關注。