采用階段更新策略加強結構進化的換熱網絡優化

趙倩倩，崔國民，肖 媛，李萬總，曹 美

（上海理工大學 能源與動力工程學院 新能源科學與工程研究所，上海 200093）

在過程工業能量系統優化領域，換熱網絡綜合方法一直是研究熱點之一［1-3］。換熱網絡的同步優化屬于混合整數非線性規劃［4］，具有求解域龐大且不規則，上下極值不穩定等特點。傳統的確定性算法易受網絡規模大小的制約，全局搜索能力弱，很難獲得相對較好的優化結果。越來越多的基于隨機技術和群體智能的啟發式方法被應用到換熱網絡優化中，如遺傳算法、微分進化、粒子群算法等［5-7］，這些算法雖然有利于優良個體的保護和遺傳，但在進化后期極易因種群的差異性過小，而導致目標函數易陷入局部最優解。肖媛等［8］提出強制進化隨機游走（RWCE）算法，該算法具有的隨機性，降低了進化后期早熟收斂弊端出現的幾率；Liu 等［9］通過對步長的研究提出拋物線函數的最大步長（ΔL）遞減調整策略來平衡RWCE 算法的全局搜索與局部搜索能力。但換熱網絡優化中依然會受到種群個體多樣性的限制，存在年綜合費用（TAC）下降緩慢或進化停滯的現象。

本工作提出了階段更新策略改進的強制進化隨機游走（PR-RWCE）算法。該算法通過階段性地隨機改變ΔL 和允許生成的最小換熱量（Qmin）對種群個體結構進行更新，增強了整型變量的進化能力和優化中產生差解的復雜性，進而促進結構進化，保持種群活力和進化種群個體的多樣性。

1 換熱網絡模型優化及RWCE 算法流程

1.1 分級超結構模型

圖1 為無分流換熱網絡的分級超結構模型［10］。由圖1 可知，熱流體由左向右為冷卻方向，冷流體由右向左為加熱方向。中間虛線的左側為第一級，右側為第二級，級數（NS）按需而定。

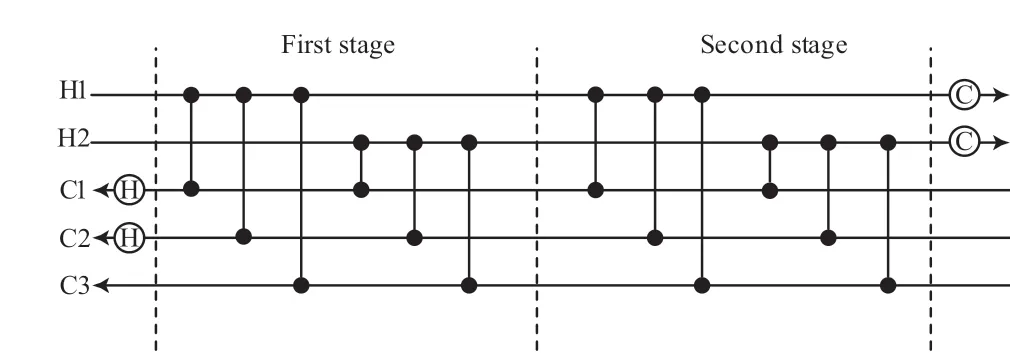
圖1 無分流換熱網絡的分級超結構模型［10］Fig.1 Hierarchical super-structure of heat exchanger networks without stream split［10］.

1.2 目標函數

以最低TAC 為優化目標，TAC 為換熱器的固定投資費用、面積費用和冷熱公用工程的運行費用之和。

1.3 RWCE 算法流程

RWCE 算法通過隨機增大或減少每個換熱單元上的換熱量協同完成連續變量（換熱單元的換熱量）和整型變量（換熱單元數）的同步優化，具體步驟如下：

1）種群初始化：隨機生成初始化種群，產生初始結構，隨機賦予換熱量（Qik）給每一個個體，見式（1）；

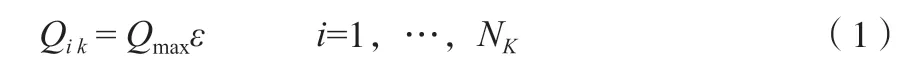
式中，Qmax為初始求解域大小，kW；ε 為（0，1）之間的隨機數。

2）個體進化：對種群中的每個個體進行變異操作，實現個體更新，見式（2）；

式中，ΔL 為最大步長；α，β 均為（0，1）的隨機數。

當某處換熱器的換熱量Qi+1，k≤ΔLη 時，消去此處的換熱器。ΔLη 為優化過程中換熱器的最小換熱量，η 為保留系數。

3）個體選擇：若變異后TAC 降低，則更新并記錄種群最優個體所對應的換熱量，否則，以一定的接受差解概率（δ）選擇更新，當隨機數rand（0，1）小于δ 時，接受當前差解進入下一次迭代；

4）終止條件：若迭代步數（IT）達到最大，則迭代終止。

2 階段更新策略的提出及效果分析

2.1 ΔL 和Qmin 對RWCE 算法優化過程的影響

表1 為以15SP 流股為例流體的物性參數［11］。令Qmin= ΔLη，參數設置：N（種群規模）=25，Qmin= 1 000 kW，δ=0.01。

2.1.1 ΔL 的影響

圖2 為不同ΔL 對進化過程的影響。由圖2 可知，當ΔL=200 kW 時，迭代25 萬次后TAC 最優解穩定在8 900 000 $/a 附近；當ΔL=30 kW 時，迭代160 萬次后TAC 降至5 298 729 $/a，但后期最低TAC 大部分時間處于“停滯”狀態；當ΔL=100 kW 時，所對應的TAC 最低，為5 208 506 $/a，但進化后期依然缺乏不斷下降的動力。因此，ΔL 的大小直接影響著進化的最優結果，決定著隨機游走時換熱量的可行域范圍及優化效率。ΔL 較大，算法的全局搜索能力增強，但局部尋優能力較低，易在局部極值附近左右跳動；ΔL 較小，有利于提高算法局部最優解的精度，但全局尋優能力較低，易陷入局部最優難以跳出。

2.1.2 Qmin的影響

圖3 為不同Qmin對進化過程的影響。由圖3可知，當Qmin=60 kW 時，TAC 呈下降趨勢，但到6 750 084 $/a 后下降停滯；當Qmin=120 kW 時，TAC 穩定在5 340 633 $/a，之后不再有明顯變化；當Qmin=90 kW 時，對應TAC 最低，為5 208 506 $/a，但在后期仍出現費用緩慢下降的現象。Qmin的大小直接影響著換熱單元的生成和消去。當ΔL不發生改變時，保留系數（η）越大，則Qmin越大，換熱單元的數目不易發生大幅度變化，同樣消去的換熱量也大，容易將換熱量較小的換熱單元消去。反之，η 越小，Qmin越小，但換熱單元的生成幾率較大，同樣消去的換熱量也小，這在進化后期會影響局部極值的精度。

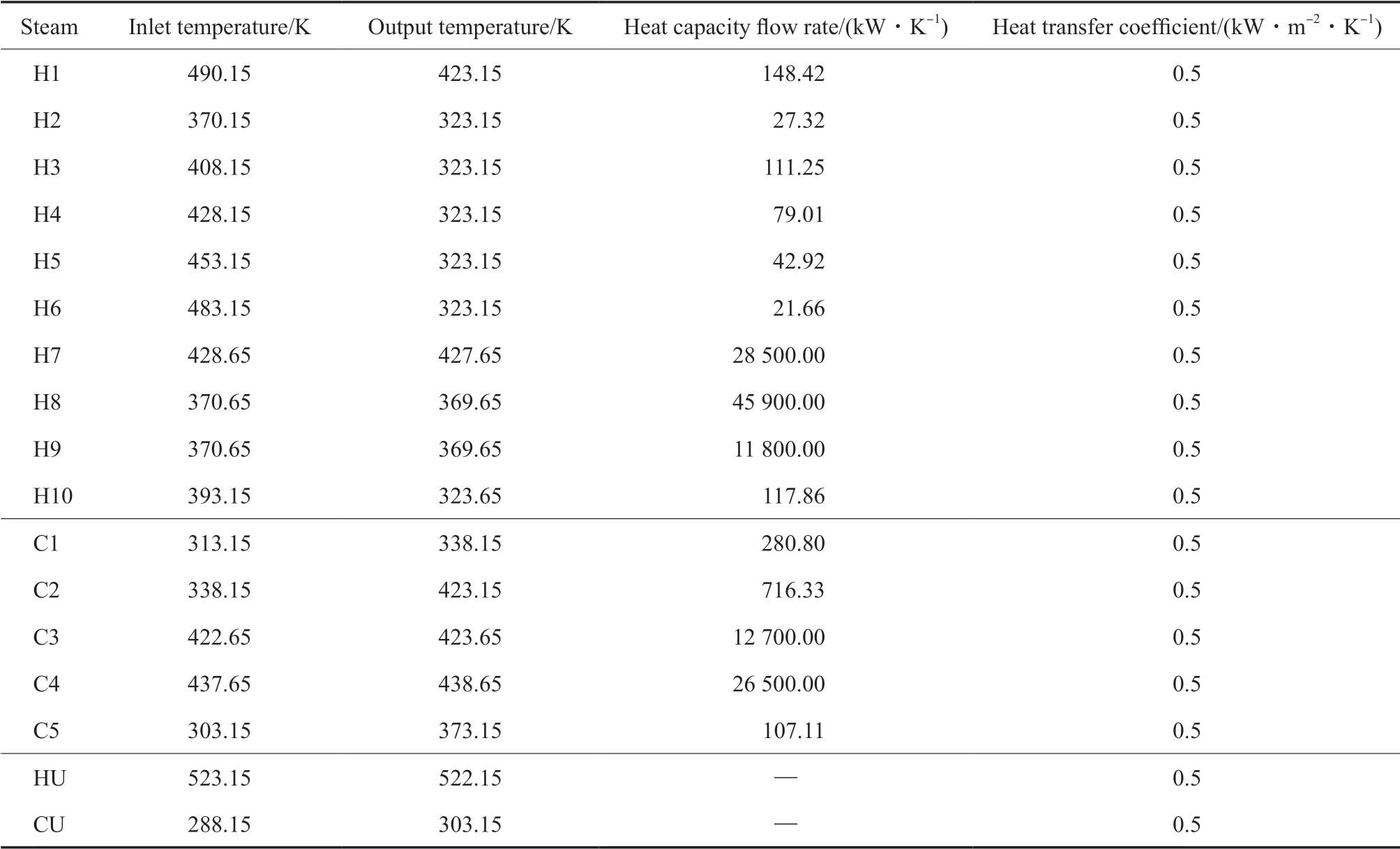
表1 15SP 流股參數［11］Table 1 Stream data of 15SP［11］

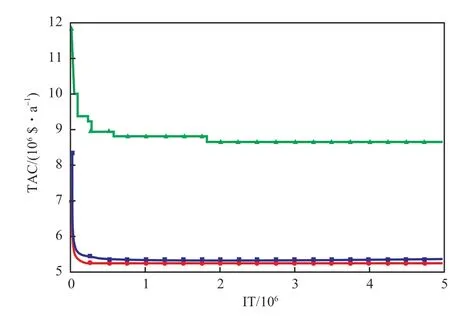
圖2 不同ΔL 對進化過程的影響Fig.2 Influence of different maximum stride length(ΔL) on evolutionary processes.

2.1.3 ΔL 和Qmin聯動影響

ΔL 和Qmin均影響著整個優化過程，將二者聯動起來，至每2 萬步或它的倍數時隨機更新一次ΔL 和Qmin，記為更新后的最大步長（ΔL*）和更新后的最小換熱量（），其他步數時保持原有的參數組不變。IT 為500 萬次的優化結果見表2。由表2 可知，相同步數下更新參數后TAC 更低（不更新參數對應的TAC 優化結果為5 208 506 $/a）。可見，更新ΔL 和Qmin可使二者在優化過程中充分發揮各自優勢，得到更好的優化結果。當換熱網絡優化陷入局部最優解時，可認為每一個換熱單元與所匹配的換熱量處于平衡狀態，此時換熱單元數目在很小的范圍內發生變化，很難突破陷入局部極值的瓶頸。定期隨機更新一次ΔL，使個體在進化變異階段已生成的換熱單元隨機增加或減少的換熱量范圍發生變化，由于新的換熱量變化使原本的平衡狀態被打破，產生新的連續變量分布。定期隨機更新一次Qmin，可增大換熱量較小的換熱單元生成和消去的機會，使換熱網絡優化過程整型變量進化能力增強，在新的結構下進一步優化，增加個體進化產生更優解的機會。

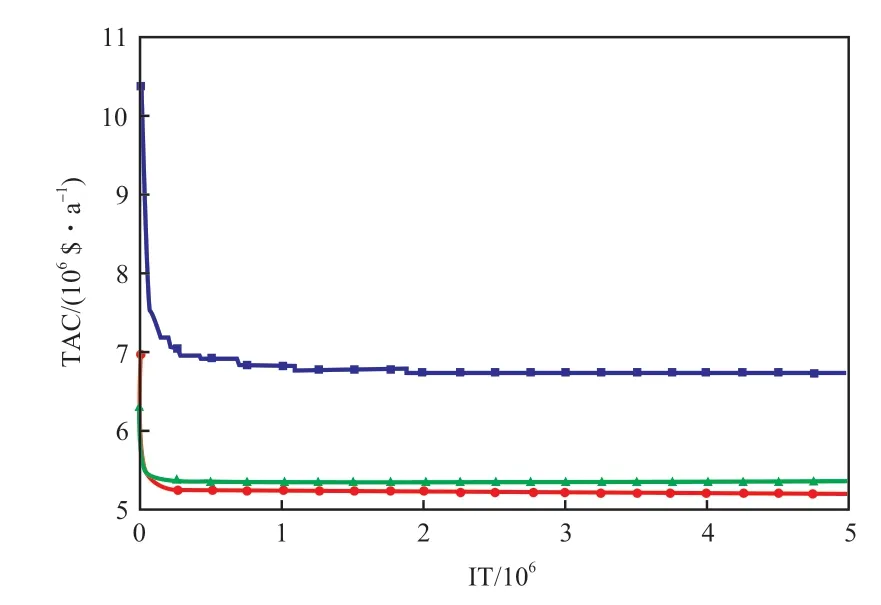
圖3 不同Qmin 對進化過程的影響Fig.3 Influence of different minimum heat(Qmin) on evolutionary processes.

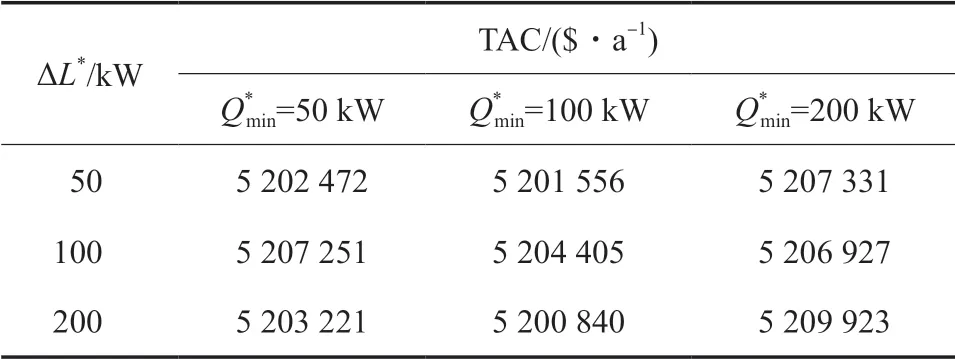
表2 更新參數后優化結果的TAC 統計Table 2 TAC statistics of optimization results after updating parameters

2.2 PR-RWCE 算法的提出

為保持種群活力和具有更好的多樣性，進一步加強結構進化能力，使優化時更易跳出局部極值尋求最優解。采用PR-RWCE 算法，通過定性設置周期（T），隨機生成ΔL*和。當IT 為T 或T的倍數時，讓本次迭代在ΔL*和下進行，否則還沿用原始的固定參數組進化，進而能夠保留原結構的原始優異性能。ΔL*和對應式（3）和式（4）：

式中，C1，C2為比例系數。

在ΔL*和Q*min下進化的個體進化有效或以一定的δ 接受更新時，個體在新的結構下繼續進化，優化結果與全局最優解比較，選擇是否更新結構。直至IT 符合終止條件，循環結束。

2.3 階段更新策略效果分析

以15SP 流股為例流體，參數設置：N=25，Qmax（初始求解域大小）=1 000 kW，δ =0.01。原始參數組中ΔL=100 kW，Qmin=90 kW，T=20 000，C1=0.1，C2=1.1。圖4 為改進前后較優新個體換熱單元數目隨IT 的變化，縱坐標為每次迭代種群中較優解的個體換熱單元數目。由圖4 可知，改進后換熱單元數目不再穩定在20 附近，而是在大范圍內隨機增大或減少，使變異后新的結構與原結構差異性增大，由此表明階段更新策略可有效地增強整型變量的進化能力。

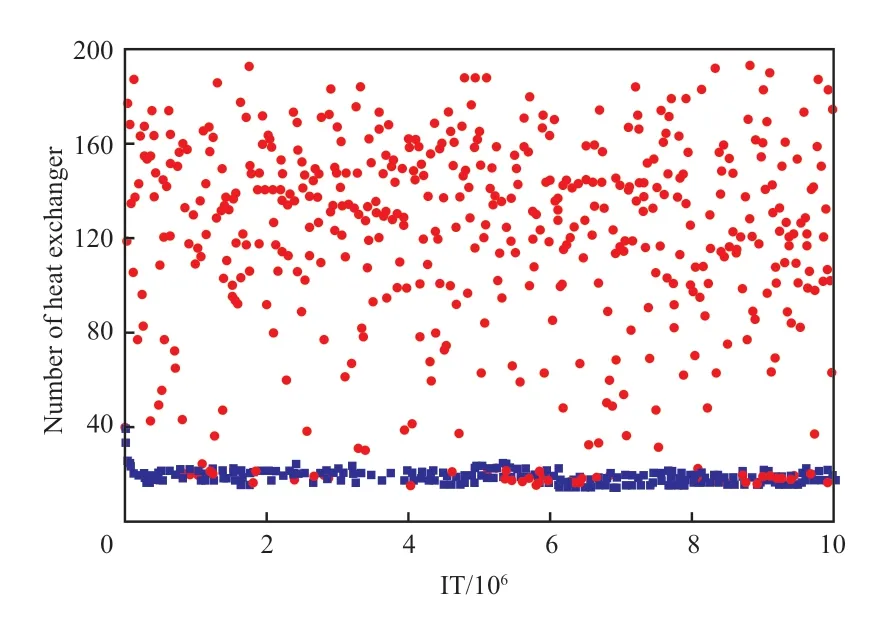
圖4 改進前后較優新個體換熱單元數目分布Fig.4 Heat exchangers units distribution of better new individuals before and after improvement.

圖5 為改進前后較優新個體的TAC 隨IT 的變化，縱坐標為每一次迭代種群中的較優解。由圖5可知，改進前較優新個體的TAC 在5 250 000 $/a附近上下跳動，改進后較優新個體的TAC 變化幅度相比改進前明顯增大，表明改進后的算法產生差解和更優解的機會增多，種群個體中差解的復雜性增強。差解以一定的概率被接受之后，新個體在新的結構下繼續進化，增加產生更優解的機會。

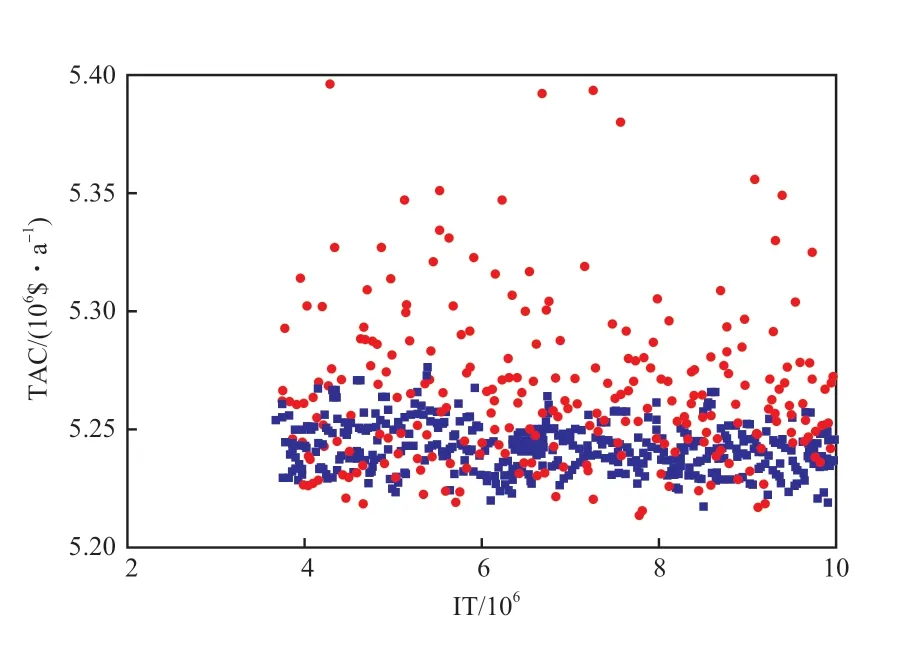
圖5 改進前后較優新個體的TAC 分布Fig.5 TAC distribution of better new individuals before and after improvement.

圖6 為改進前后TAC 變化曲線。

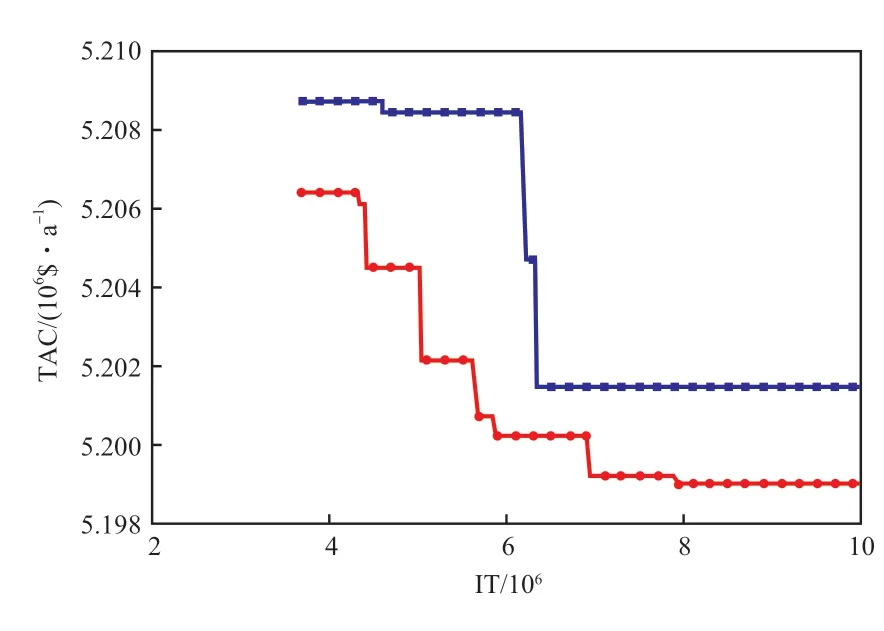
圖6 改進前后TAC 變化曲線Fig.6 TAC changing curves before and after improvement.

由圖6 可知，改進后的進化過程中尤其是在進化后期TAC 下降點增多。改進后算法的TAC 明顯降低，并使TAC 朝著更低的方向進行。迭代至630 萬次附近時，RWCE 算法在優化過程中TAC下降驟變，相比之下改進后的算法TAC 下降趨勢較穩定，具有更好的魯棒性。迭代至107次時，改進前的TAC 優化結果是5 201 524 $/a，改進后的TAC 優化結果是5 199 067 $/a，下降了12 457 $/a。這表明PR-RWCE 算法為換熱網絡的整個優化過程提供了TAC 下降的動力，階段更新策略具有可行性。

3 算例分析

3.1 算例1

選用15SP 流股［11］，其中包括10 股熱流體，5 股冷流體，各冷熱流股的物性參數見表1。參數設置：N=25，Qmax=1 000 kW，δ =0.01。固定參數組中ΔL=100 kW，Qmin=90 kW，T=20 000，定期使ΔL*和在一定范圍內隨機生成，其中，C1=0.1，C2=1.1。加入策略后最終優化結果為5 169 883 $/a，與文獻［12］相比降低了443 400 $/a。表明該策略使算法具有更強的跳出局部最優解的能力。表3 為算例1 與文獻的對比結果。圖7 為算例1 優化結果相對應的結構。

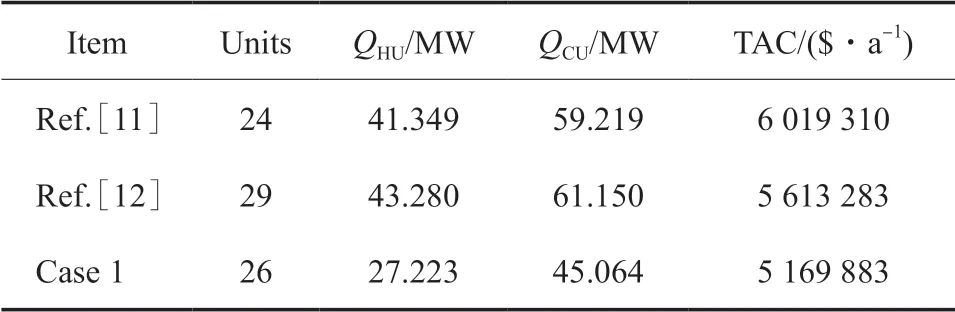
表3 算例1 與文獻對比結果Table 3 Comparison between the results of case 1 and literature data

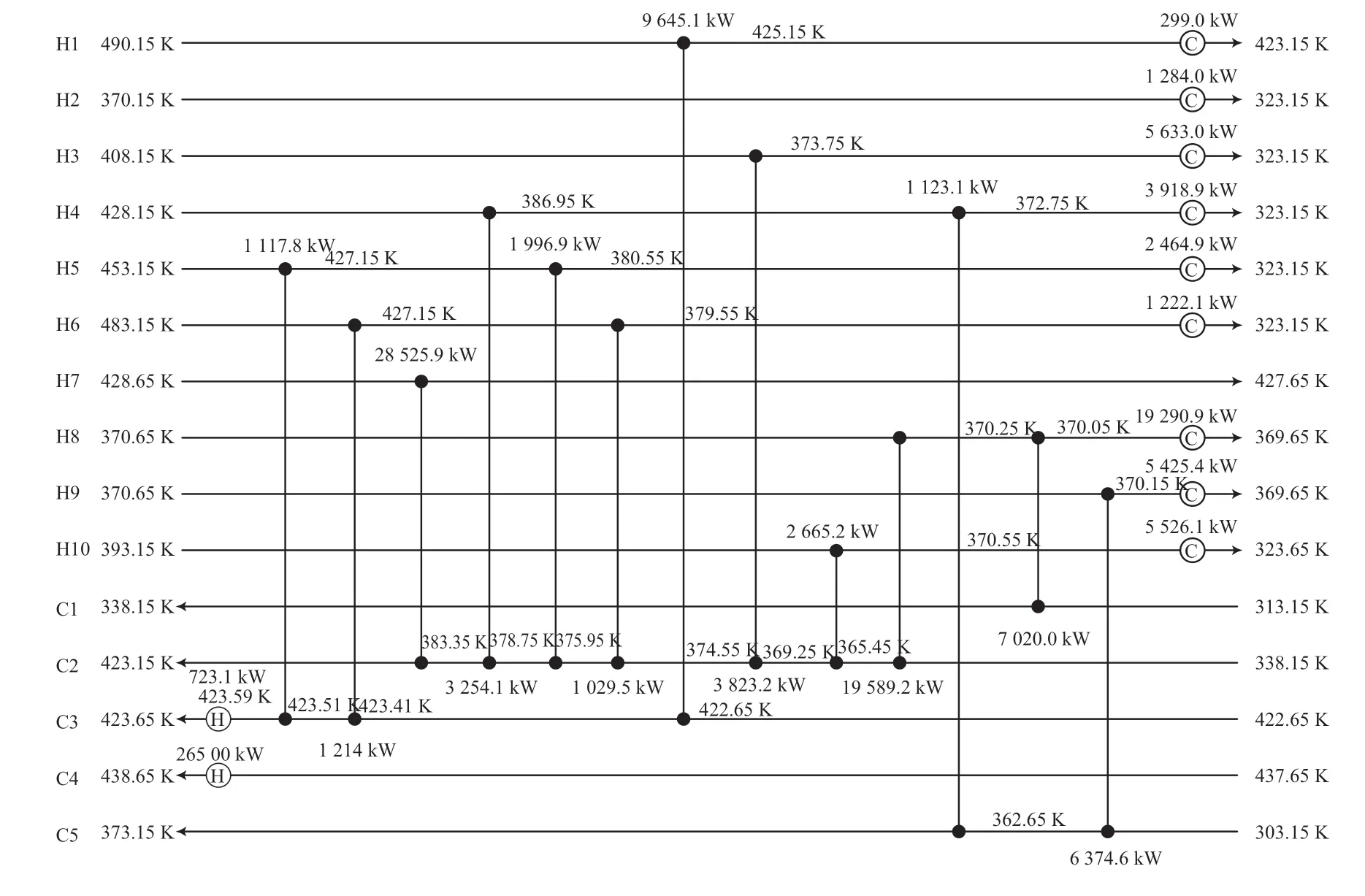
圖7 算例1 優化結果相對應的結構Fig.7 Case 1 corresponding structure of the optimization result.

3.2 算例2

選用20SP 流股［13］，物性參數見表4。參數設置：N=25，NS=4，Qmax=2 000 kW，δ =0.01。固定參數組中ΔL=100 kW，Qmin=90 kW，T=10 000，定 期 使ΔL*和在一定范圍內隨機生成，其中，C1=0.1，C2=1.1。加入策略后算例2 的TAC 優化結果為1 418 925 $/a，比文獻［14］降低了29 159 $/a。表5 為算例2 與文獻對比結果。圖8 為算例2 優化結果相對應的結構。

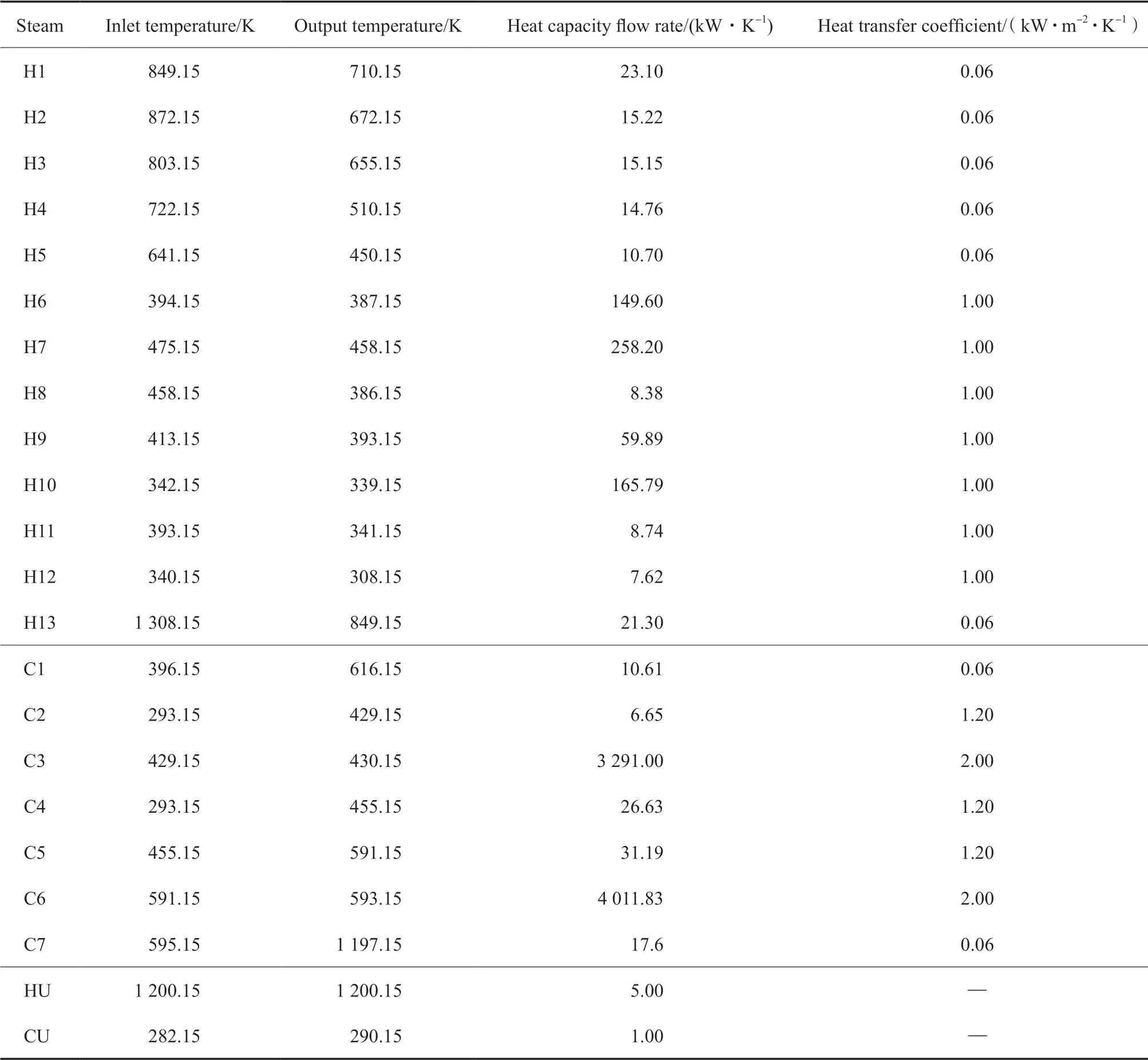
表4 20SP 流股參數［13］Table 4 Stream data of 20SP［13］

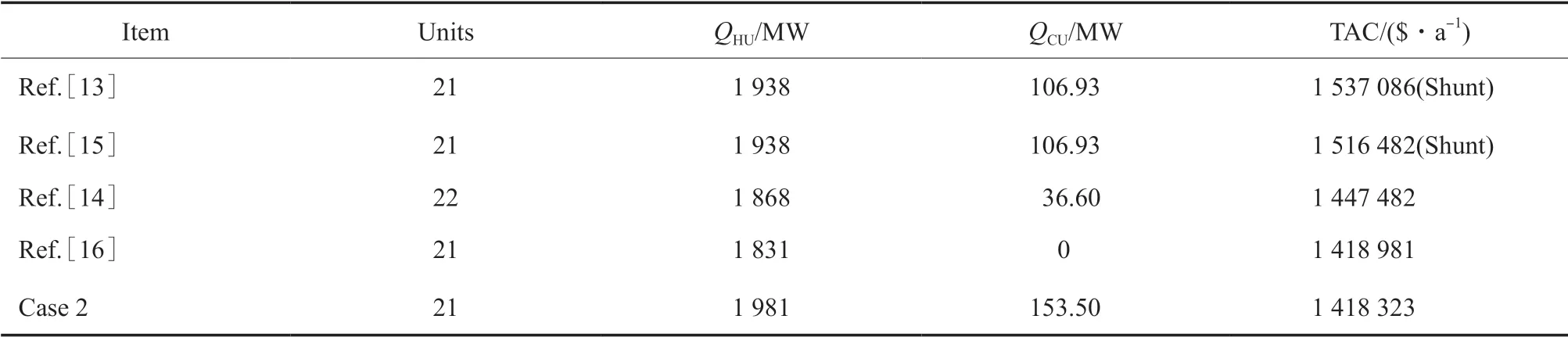
表5 算例2 與文獻對比結果Table 5 Comparison between the results of case 2 and literature data

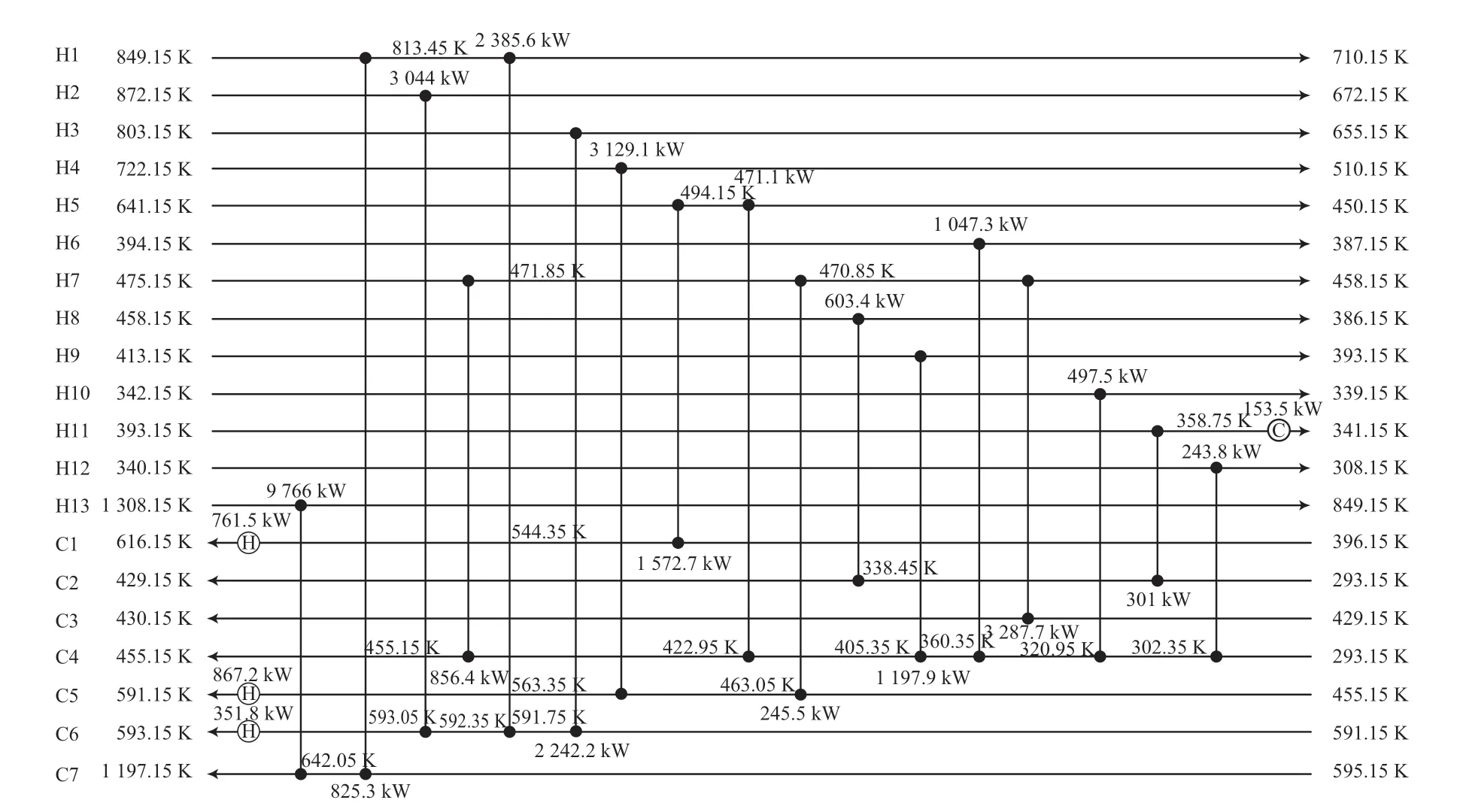
圖8 算例2 優化結果相對應的結構Fig.8 Case 2 corresponding structure of the optimization result.

4 結論

1）改進后的PR-RWCE 算法將ΔL 和Qmin在一定范圍內隨機生成新的數值，使得原本在優化全程固定不變的參數發生階段性變化。二者的聯動調整在優化中發揮各自優勢，增強了結構進化能力。

2）在優化過程中新個體的整型變量階段性地發生變化，增加了新個體產生差解和優解的可能性，也增加了新結構與原始結構的差異性，以此保持種群活力。該方法既能夠保留原結構的原始優異性能，又能整體改變結構，結構變化后的換熱量重新分配，使換熱網絡優化產生更優解的機會增加。

3）改進后的PR-RWCE 算法魯棒性增強，使優化過程更加穩定高效，能很好地在龐大且不規則的求解域中尋找到更好的解。另外種群多樣性的增加使算法在優化中更易跳出局部極值，獲得更強的全局搜索能力。