積分變換中卷積的微分性質(zhì)

馬紀(jì)英，王 潮，姜文鵬

(石家莊郵電職業(yè)技術(shù)學(xué)院，河北 石家莊 050021)

卷積是分析數(shù)學(xué)中一種重要的運(yùn)算，是一種積分變換的數(shù)學(xué)方法，它是通過兩個(gè)函數(shù)生成第三個(gè)函數(shù)的一種數(shù)學(xué)算子.卷積與Fourier變換，以及Fourier變換的特殊形式Laplace變換，都有著密切的關(guān)系，尤其是卷積定理，把函數(shù)卷積的積分變換和函數(shù)積分變換的乘積聯(lián)系起來，大大簡化了卷積的計(jì)算量，使得Fourier分析中許多問題的處理得到簡化.同樣，卷積自身又有著諸如數(shù)乘、微分、積分、不等式等各種運(yùn)算性質(zhì)以及運(yùn)算規(guī)律，其中卷積的微分性質(zhì)尤其處于顯要位置.

1 卷積的概念和微分性質(zhì)

1.1 Fourier變換卷積的概念和微分性質(zhì)[1]

若已知函數(shù)f1(t)，f2(t)，則積分

稱為f1(t)與f2(t)的卷積，記為f1(t)*f2(t)，即

卷積運(yùn)算滿足：交換律、結(jié)合律、對加法的分配律；還具有數(shù)乘、微分、積分、不等式等基本性質(zhì).其中微分性質(zhì)如下：

1.2 Laplace變換卷積的概念和微分性質(zhì)

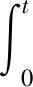
同F(xiàn)ourier變換的卷積一樣，Laplace變換的卷積運(yùn)算也滿足：交換律、結(jié)合律、對加法的分配律；也具有數(shù)乘、微分、積分、不等式等基本性質(zhì).其中微分性質(zhì)如下：

2 微分性質(zhì)的證明

2.1 Fourier變換微分性質(zhì)的證明

由卷積運(yùn)算的交換律f1(t)*f2(t)=f2(t)*f1(t)，可得

2.2 Laplace變換微分性質(zhì)的證明

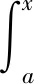
設(shè)φ(x)，ψ(x)在區(qū)間[a,b]上連續(xù)，

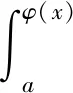
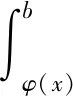
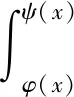
證明：根據(jù)引理，令f(τ,t)=f1(τ)f2(t-τ)，則有

同樣，由卷積運(yùn)算的交換律f1(t)*f2(t)=f2(t)*f1(t)，可得

3 微分性質(zhì)的應(yīng)用

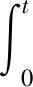
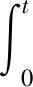
解令[y(t)]=Y(s).由

取其逆變換可得y(t)=?-1[Y(s)]=sint+y(0)cost，

當(dāng)t=0時(shí)，有y(0)=0.因此，方程的解為y(t)=sint.

4 小結(jié)

卷積和卷積定理是Fourier變換和Laplace變換的一類非常重要的性質(zhì)，在求解積分變換的逆變換，微分、積分方程，偏微分方程的過程中發(fā)揮著巨大的作用，雖然卷積并不是很容易計(jì)算，但是卷積定理和卷積的運(yùn)算性質(zhì)提供了卷積計(jì)算的簡便方法，化卷積運(yùn)算為乘積運(yùn)算，這就使得卷積在線性系統(tǒng)分析中稱為特別有用的方法.此外，卷積運(yùn)算在統(tǒng)計(jì)學(xué)、概率論、聲學(xué)、電子工程與信號處理、物理學(xué)等工程和數(shù)學(xué)上都有很多應(yīng)用.