基于多目標蝗蟲優化算法的移動機器人路徑規劃

黃超 梁圣濤 張毅 張杰

摘 要：在靜態多障礙物環境下的移動機器人路徑規劃問題中，粒子群算法存在容易產生早熟收斂和局部尋優能力較差等缺點，導致機器人路徑規劃精度低。為此，提出一種多目標蝗蟲優化算法（MOGOA）來解決這一問題。根據移動機器人路徑規劃要求將路徑長度、平滑度和安全性作為路徑優化的目標，建立相應的多目標優化問題的數學模型。在種群的搜索過程中，引入曲線自適應策略以提高算法收斂速度，并使用Pareto最優準則來解決三個目標之間的共存問題。實驗結果表明：所提出的算法在解決上述問題中尋找到的路徑更短，表現出更好的收斂性。該算法與多目標粒子群（MOPSO）算法相比路徑長度減少了約2.01%，搜索到最小路徑的迭代次數減少了約19.34%。

關鍵詞：路徑規劃;移動機器人;蝗蟲優化算法;多目標

中圖分類號：TP242.6;TP23

文獻標志碼：A

Abstract： In the mobile robot path planning problem in static multi-obstacle environment， Particle Swarm Optimization （PSO） algorithm has the disadvantages of easy premature convergence and poor local optimization ability， resulting in low accuracy of robot path planning. To solve the problem， a Multi-Objective Grasshopper Optimization Algorithm （MOGOA） was proposed. The path length， smoothness and security were taken as path optimization targets according to the mobile robot path planning requirements， and the corresponding mathematical model of multi-objective optimization problem was established. In the process of population search， the curve adaptive strategy was introduced to speed up the convergence of the algorithm， and the Pareto optimal criterion was used to solve the coexistence problem of the above three targets. Experimental results show that the proposed algorithm finds shorter paths and shows better convergence while solving the above problems. Compared with the Multi-Objective Particle Swarm Optimization （MOPSO） algorithm， the proposed algorithm has the path length reduced by about 2.01 percentage， and the number of iterations reduced by about 19.34 percentage.

Key words： path planning; mobile robot; grasshopper optimization algorithm; multi-objective

0 引言

在移動機器人導航系統中，規劃一條最優路徑成為近年來一個重要的課題，引起了眾多研究者的關注[1]。移動機器人的最優路徑規劃問題，就是依據某些優化準則（工作代價最小如行走路線最短等），在其工作空間中找到一條從起始狀態到目標狀態并且能避開障礙物的最優路徑。

當前在移動機器人路徑規劃中常用的粒子群（Particle Swarm Optimization， PSO）算法[2]屬于進化算法的一種，與模擬退火算法相似，它也是從隨機解出發，通過迭代尋找最優解，利用適應度來評價解的品質，并通過追隨當前搜索到的最優值來尋找全局最優。該算法的優點是實現容易、精度高、收斂快;但容易產生早熟收斂，局部尋優能力較差。賈會群等[3]為了提高路徑規劃的精度，對基本粒子群算法進行改進，將各階段慣性因子和加速因子使用三角函數方式進行自適應調節，并且引入了雞群算法中的母雞更新方程和小雞更新方程，提高了算法的搜索能力。多目標進化算法結合粒子群算法的研究在國內外已經取得了研究成果，2018年楊景明等[4]將帕累托（Pareto）解集與“多點變異”引入粒子群算法中，避免了算法陷入早熟收斂。但是多目標粒子群（Multi-Objective PSO， MOPSO）算法在解集分布性、收斂性方面仍然存在不足。

近年來，一些學者提出了元啟發式方法[5]來克服經典方法的不足。特別是在大范圍和高自由度問題中，蝗蟲優化算法（Grasshopper Optimisation Algorithm， GOA）[6]由Saremi等于2017年1月提出。蝗蟲算法相較于粒子群算法[7]具有良好的全局搜索能力和收斂速度。因為該算法的提出時間較短，目前對該算法的研究文獻較少，現在主要是對算法的應用場景和算法自身的改進兩個方面。2017年，Tumuluru等[8]利用蝗蟲優化算法更新癌癥分級問題中神經網絡的權值;2017年，Barman等[9]將蝗蟲優化算法應用于電力負荷預測問題中的向量機參數估計問題中。在算法改進的方面，2017年Mirjalili等[10]提出了一種多目標蝗蟲優化算法（Multi-Objective Grasshopper Optimization Algorithm， MOGOA）;2018年閆旭等[11]將量子旋轉門引入基本蝗蟲優化算法，并應用到車間調度問題;2017年，程澤新等[12]首次將蝗蟲算法應用到解決無人機（Unmanned Aerial Vehicle， UAV）三維航跡規劃問題中，并能夠規劃出一條較優路徑。但由于UAV所處的環境障礙物較少、環境簡單，將蝗蟲優化算法引入移動機器人路徑規劃當中，其所處的環境相較于空中環境要復雜，所以容易陷入局部最優和收斂精度不足。本文提出應用曲線調整策略自適應更新c參數來平衡局部搜索能力和全局搜索能力，提高算法的搜索能力;然后引入多目標最優方法來獲得合適的導航路線;最終提高了算法的收斂性及穩定性。

為了平衡種群搜索和開發，需要用c參數動態調整蝗蟲群的勘探和開發，同時應減小與迭代次數成比例的舒適區，采用曲線自適應更新策略剛好彌補這一不足。式（15）中采用的是余弦自適應方式，余弦函數在開始和結束時下降速率小，余弦自適應調整參數c在前期的值比式（16）線性調整的值大，增加蝗蟲的搜索能力，隨著迭代次數的增加，搜索的效率提高，蝗蟲群會朝目標位置附近收斂;后期c參數的比式（16）中的小，可以縮小蝗蟲的搜索范圍，增加蝗蟲的局部搜索能力。這些特點使得在不陷入局部最優的情況下，極大地提高了算法的收斂速度。

2）添加外部儲存archive集來保存搜索過程中的非支配解。每次迭代過程對支配解集B進行位置更新，并對更新后的支配解集B與archive中的粒子進行比較，若xi∈B，且xj∈archive，使得xi支配xj，則刪除xj，使xi加入A更新外部archive，全局最優解從外部儲存archive中選出。具有最短和最光滑路徑約束的多目標路徑規劃優化模型的主要目標是獲得多目標Pareto最優解，因此，根據決策空間可行解集λ和Pareto最優解F（p*），

MOGOA的主要目的是確定通過確定保存在archive中的Pareto最優解集X的支配關系，

若新的候選解優于當前解，則優勝劣汰，不斷更新當前解和全局最優解解。

2.2.2 算法流程

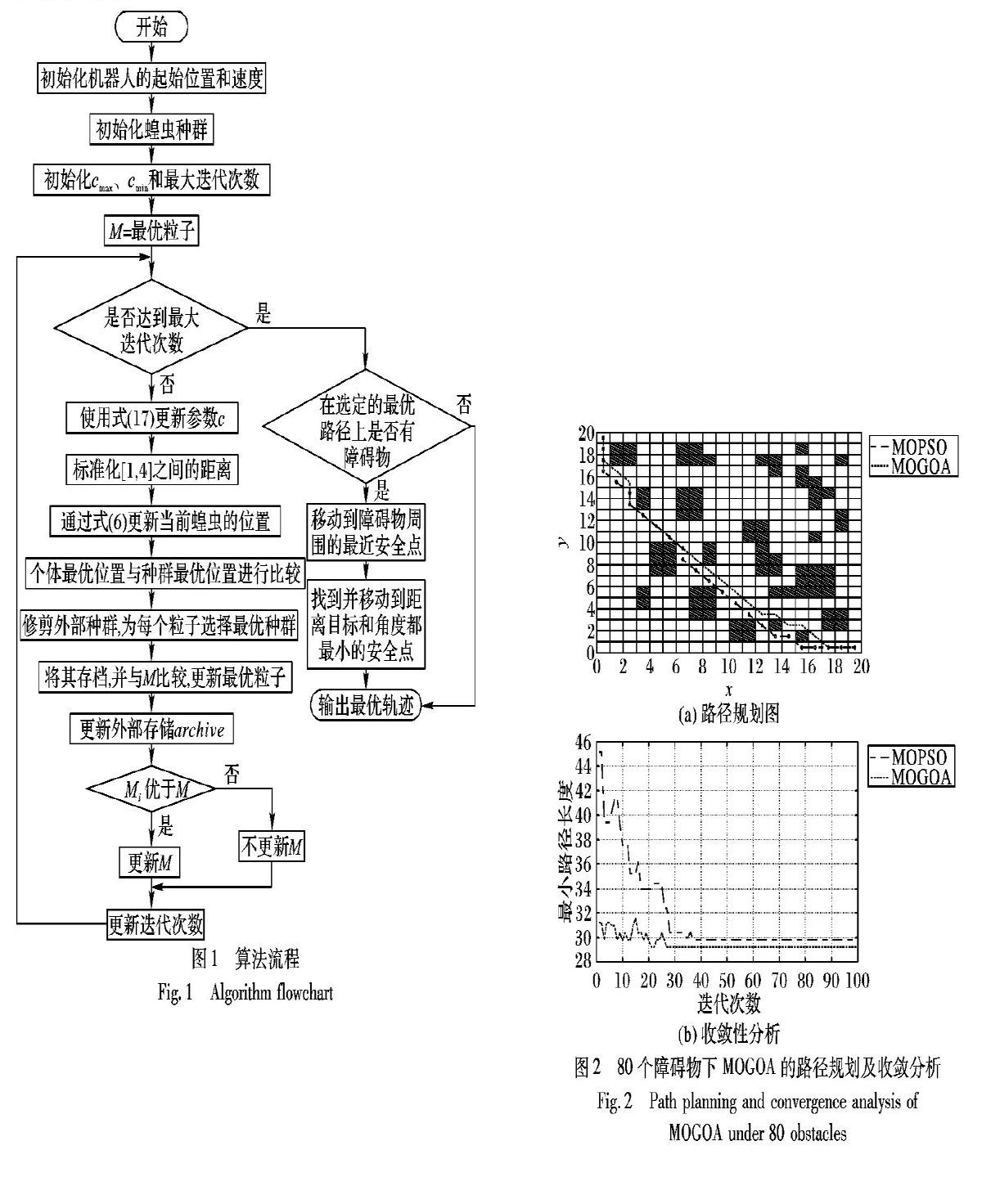
算法流程見圖1，具體算法步驟如下：

1）初始化蝗蟲種群的初始位置、種群規模及算法中的各參數，如：cmax、cmin、最大迭代次數;

2）計算蝗蟲群每個搜索個體的適應度值，并找出當前全局最優解;

3）M=最優粒子;

4）使用式（17）更新參數c;

5）標準化區間在[1，4]的蝗蟲之間的距離;

6）通過式（6）更新當前粒子的位置;

7）修剪外部種群，為每個粒子選擇全局最優位置;

8）計算并選擇每個粒子的個體歷史最優位置和種群最優位置進行比較;

9）將每個粒子的最優位置粒子存檔，與M進行比較，更新最優粒子;

10）根據新的非支配解與已存檔的非支配解的比較，更新外部存儲archive;

11）移動機器人繞開障礙物，選擇距離目標最安全的點，輸出最優軌跡。

2.2.3 評價指標該算法在多個障礙物且數目不同的環境中進行了性能和效率的測試。

第一個測試標準是最優解錯誤率（Error Ratio， ER）[16]，本文使用一個標準來評估多目標優化算法的性能，測量解是否為實際Pareto最優解的概率，ER是評價帕累托最優解算法精度的一個很好指標。計算方法如下：

其中：m為Pareto最優解的個數。當xi=0時，得到的解是Pareto最優解;否則，xi=1。

第二個測試標注是最優解覆蓋率SCM（Set Coverage Metric）[17]，計算公式如下：

其中：A和B是目標空間中的兩個非支配解，即覆蓋率是B中的非支配解被A中非支配解覆蓋的個數在B中所占比例[18];|B|表示集合B中元素的個數;表示Pareto占優。

由式（19）可知，SCM（A，B）∈[0，1]。SCM（A，B）值越大，表示解集A覆蓋解集B的程度越高，也就是說A優于B的程度也越高，當SCM（A，B）>SCM（B，A）時，表示解集A覆蓋解集B的比例要小于解集B覆蓋解集A的比例，說明解集A中的非支配解要優于解集B中的非支配解集。

3 實驗與結果分析

仿真實驗所用軟件是Matlab R2014，在具有Intel i7處理器（2.8 GHz）CPU和16 GB RAM的聯想筆記本上實現。最大迭代次數為100，cmax=1，cmin=0.00001。MOPSO的參數組合為：c1=c2=1.5，權重系數為0.8，最大最小權重系數分別為0.2和0.9。在環境1和環境2中，蝗群規模和粒子群規模均設置為500。

為了驗證該算法相較于粒子群算法的優越性，與文獻[19]中的多目標粒子群（MOPSO）算法進行比較。實驗環境均采用20×20方格，初始位置的坐標為（0，20），目標位置的位置為（20，0），黑色陰影部分表示環境中的障礙物。

在環境1中，將障礙物的數量設置為80，圖2是MOGOA與MOPSO在80個障礙物數目下的路徑規劃結果和收斂性分析。

在環境2中，將障礙物的數量增加為100。圖3是MOGOA與MOPSO在100個障礙物數目下的路徑規劃結果和收斂性分析。

在環境1和環境2不同的障礙物數目下得到的路徑長度和迭代次數進行比較分析。從表1可看出，不論在環境1還是環境2中，MOGOA在路徑長度均小于MOPSO，且收斂速度較快。多目標蝗蟲群算法（MOGOA）與多目標粒子群（MOPSO）算法相比路徑長度縮短了約2.01%，搜索到最小路徑的迭代次數相比減少了約19.34%。本文算法提高了蝗蟲優化算法的搜索能力，同時也提高了算法的收斂速度。

表2為MOGOA和MOPSO在ER和SCM兩個指標的運算結果，為通過算法10次獨立運行后獲得。從表2可以明顯看出，MOGOA的解集錯誤率都明顯低于MOPSO，同時在解集覆蓋度SCM（MOGOA，MOPSO）也都大于SCM（MOPSO，MOGOA），表明MOGOA在Pareto最優解精度方面優于MOPSO。因此，實驗結果表明，MOGOA能很好地收斂于帕累托最優解。與MOPSO相比，本文算法在較短的時間內獲得了最優解和最優路徑，說明該算法在尋找最短路徑、收斂性方面的性能優于PSO算法。

為了驗證MOGOA的性能，將MOPSO和MOGOA在Schaffer2和ZDF4兩個多目標測試函數上進行對比，它們的最優邊界收斂對比結果如圖4所示。Schaffer2和ZDF4具有不同的復雜度情況：Schaffer是一個一維兩個極小值點的函數;ZDT4是一個多維多個極小值點的函數。

[11] 閆旭， 葉春明.混合蝗蟲優化算法求解作業車間調度問題[J]. 計算機工程與應用， 2019， 55（6）： 257-264. （YAN X， YE C M. Hybrid grasshopper optimization algorithm solves job-shop scheduling problem [J]. Computer Engineering and Applications 2019， 55（6）： 257-264.）

[12] 程澤新， 李東生， 高楊.基于蝗蟲算法的無人機三維航跡規劃[J]. 飛行力學， 2019， 37（2）： 46-50， 55. （CHENG Z X， LI D S， GAO Y. UAV three-dimensional path planning based on grasshopper algorithm[J]. Flight Dynamics， 2019， 37（2）： 46-50， 55.）

[13] HUA Y， JIN Y， HAO K. A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts[J]. IEEE Transactions on Cybernetics， 2019， 49（7）： 2758-2770.

[14] THABIT S， MOHADES A. Multi-robot path planning based on multi-objective particle swarm optimization[J]. IEEE Access， 2018， 7： 2138-2147.

[15] MAC T T， COPOT C， TRAN D T， et al. A hierarchical global path planning approach for mobile robots based on multi-objective particle swarm optimization[J]. Applied Soft Computing， 2017， 59： 68-76.

[16] COELLO C A C， LAMONT G B， van VELDHUIZEN D A. Evolutionary algorithms for solving multi-objective problems[M]. Boston： Springer， 2002.

[17] SHIM M， SUH M， FURUKAWA T， et al. Pareto-based continuous evolutionary algorithms for multiobjective optimization[J]. Engineering Computations， 2002， 19（1）： 22-48.

[18] FENG W， ZHANG L， YANG S， et al. A multiobjective evolutionary algorithm based on coordinate transformation[J]. IEEE Transactions on Cybernetics， 2019， 49（7）： 2732-2743.

[19] DI L， ZHENG Z， XIA M. Robot path planning based on an improved multi-objective PSO method[C]// Proceedings of the 2016 International Conferenceon Computer Engineering， Information Science & Application Technology. Paris： Atlantis Press， 2016： 496-501.