“人教版”“四邊形”教學方法探究

摘 ? 要:長方形、正方形是最基本的平面幾何圖形,是學習三角形、平行四邊形、梯形等平面圖形的基礎。文章通過對相關教材的分析,提出了在教學中多角度利用點子圖素材,開展活動探究,不斷建構完善長方形正方形的特征。
關鍵詞:長方形;正方形;點子圖;活動
作者簡介:陳樂樂,浙江省溫州市籀園小學教師,研究方向為小學數學教學。(浙江 ?溫州 ?325000)
中圖分類號:G623.5 ? ? 文獻標識碼:A ? ? ?文章編號:1671-0568(2019)23-0105-02
“人教版”三年級上冊中的“四邊形”教學內容起承上啟下的作用,所以教材內容編排、新舊教材的變化、教師該如何根據教材變化進行有效的教學,都需要重視。
一、教材編寫及變化情況
筆者翻閱了2003版本與2013版本的“四邊形”的教學內容,發現教材在內容上有較大的改變。
1. 單元標題呈現不同。2003版單元標題為“四邊形”,安排在第三單元“多位數乘一位數”之前,而2013版單元標題為“長方形和正方形”,安排在第七單元“多位數乘一位數”之后。由此可見,變化有:內容凸顯長方形正方形;習題設置范圍加大,素材更豐富。
2. 學習素材呈現不同。2003版教材例題中學習材料呈現多個四邊形,并為分類做準備,讓學生在分類中認識不同四邊形的特征。2013版本只呈現長方形和正方形,重點讓學生主動探究歸納長方形和正方形的特征,使學生對它們的認識由表象到實質。
2003版本中只出現一次用釘子板圍四邊形的練習,2013版本中出現一次用點子圖畫四邊形,還有一次是用格子圖畫長方形和正方形。提供的素材不同,操作方法也不同。從實踐操作看,釘子板上圍四邊形,只要一圍自然而然就產生了直邊和角,所以學生對于四邊形的認識就是一種感知認識;而2013版本的在點子圖上或者格子圖上畫,學生要邊操作邊思考怎么畫產生角和直邊,對于學生認識四邊形,特別是認識長方形、正方形的特征有直接的體驗。
二、教學前學生情況
新舊教材中,變化之一就是出現了點子圖,那點子圖對學生的實際學習有什么正遷移或者負遷移呢?教學前有如下思考:①點子圖為學生畫四邊形提供支點,但會不會限制學生的思維,使學生看到點子圖只會想到長方形和正方形?②點子圖上的點是不是更能凸顯四邊形的特征?③點子圖是否可以規范學生的操作活動?
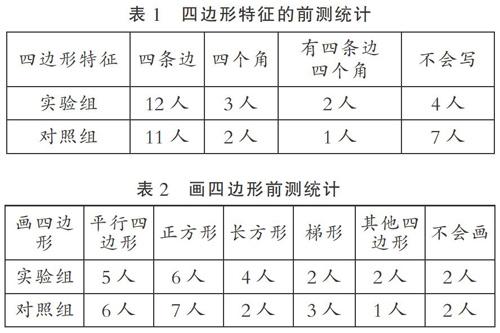
帶著這些疑問,筆者進行了前測并進行了分析。將全班42人分成兩大組,每組21人,一組同學當實驗組,一組是對照組。前測題目如下:①實驗組觀察點子圖上的四邊形說一說四邊形的特征;對照組根據白紙上的四邊形說一說四邊形的特征。②實驗組在點子圖上畫四邊形,對照組在白紙上畫四邊形。
結果分析如下(見表1、表2):
由前測結果可以看出:①讓學生畫四邊形點子圖不僅不會帶來負遷移,更是規范了學生的畫法;但對于認識四邊形特征并沒有特別明顯的優勢。②部分學生對于四邊形有一定的了解,但他們所熟悉的知識是零散的,沒有架構起零散的知識系統。
三、四邊形認識的教學思考
1. 關注知識的前后關聯,適當調整教學目標。在一年級下冊,學生學過簡單平面圖形的認識,對于不同圖形的特征有一定的了解。基于此,教師結合前測將2013版教材三年級上冊的“四邊形”內容定為認識四邊形,特別是認識長方形和正方形,重點是對長方形和正方形特征的理解。教學目標的調整如下:
(1)知識與技能:讓學生經歷多種四邊形的認識,尋找共性,概括四邊形的基本特征并能辨析四邊形;在活動探究中明晰長方形、正方形的特征,能從邊、角兩個維度加以概括。
(2)過程與方法:讓學生經歷“提出問題→大膽猜想→實驗驗證→得到結論”這一探究過程,引導學生主動觀察、實驗、猜測、驗證、推理與交流等。
(3)情感態度與價值觀:培養學生空間想象能力,感受數學的嚴密性,激發學生學習數學的興趣。
2. 巧用點子圖,感知四邊形特征。點子圖是由一行行、一列列相互對齊的點組成,每行、每列點與點之間的距離都相等。只有點沒有線,能擴大學生的思維空間,所以借助點子圖來讓學生認識四邊形尤為巧妙。四邊形的特征“封閉圖形”“四個角”“四條直邊”是學生認識四邊形、判斷四邊形的主要抓手。
(1)“四條直邊”的認識。“四條直邊”本質就是線段,可以度量長度,而點子圖一個個點,形象直觀地展現了這個特征,橫豎斜的點子連接,有長度有方向,使學生對邊的認識上升到線段。
(2)“四個角”的認識。從一點引出兩條射線組成的圖形就是角,而點子圖里的一個個點,讓學生認識四個角有點可依。
(3)“封閉圖形”。點子圖的前身就是格子圖,格子圖的密鋪性促使點子圖也具有該特征,點子圖上一個個密鋪的圖形,使學生對封閉圖形的認識更清晰。
3. 重視動手操作,完善知識結構。發展空間觀念是“幾何與圖形”領域的重要目標之一,而空間觀念是一種數學思考,這種數學思考必須有豐富的、形象的體驗為基礎,并在自主性的探究過程中得以發展。
因此,教師應設置實踐活動,幫助學生一步一步構建長方形和正方形,讓思維有螺旋式上升的梯度。筆者設置了如下活動:
(1)打破固有的思維。按照學生對于四邊形的認識,長方形、正方形是有4條邊,那是不是一定就需要四條邊呢?給定一條邊能確定長方形或者正方形嗎?學生在操作中感受到,一條邊不能確定一個長方形,長方形不唯一。但是,能確定一個唯一的正方形,感受正方形四條邊相等、四個角都是直角的特征。
(2)樹立全新的思維。再給定兩根②號小棒,兩根③號小棒(長度跟①號小棒一樣),至少需要再選幾根就能確定一個長方形?選1根②號會怎么樣?選1根③號呢?讓學生在操作中感知只要知道一條長一條寬就能確定一個長方形,從而掌握長方形對邊相等、四個角都是直角的知識。
從“立—破—立”,讓學生的思維在不斷的調整中,建立長方形、正方形的思維模型,在探究中不斷完善長方形和正方形的特征,在理解中感知長方形、正方形的特性。關注體驗的形式和思考,可以幫助學生在頭腦將表象與長方形、正方形特征之間建立聯系。
參考文獻:
[1] 葛素兒.方寸之間 ?獨具一格——方格圖在第一學段數學學習中的應用策略[J].教學月刊(數學小學版),2016,(11).
[2] 程佳麗.基于“格子圖”的幾何直觀培養策略[J].教學月刊(數學小學版),2015,(4).
[3] 于蓉.小學數學“圖形與位置”教材內容比較與分析[J].小學數學教育,2018,(20).
責任編輯 錢娜

