基于特征類型概率剪枝查詢的算法研究
占美星 范少帥 周鵬

摘 要:針對不確定對象的最近鄰反向查詢沒有考慮多種特征類型而不能滿足復雜的應用場景的問題,提出了基于限界剪枝和概率剪枝的多類型概率最近鄰反向(Multiple types probabilistic nearest neighbor reverse,MTPNNR)查詢算法。限界剪枝利用最小耗費來修剪不可行解或者非最優解對象;概率剪枝是基于概率分布模型和不確定對象分解的策略,根據概率各個閥值和剪枝的深度來控制需要剪枝的精度。與原始基于定義的算法相比較,MTPNNR查詢算法在CPU資源開銷方面有比較大的優勢,能夠完成在較大數據復雜等環境下的查詢。基于實驗結果顯示,MTPNNR算法在離散型的數據集和不確定數據集上有比較好的查詢效率。
關鍵詞:不確定對象;最近鄰反向查詢;概率剪枝;限界剪枝
1 緒論
在數據集中,其不確定性是一個比較新的領域,并且一直受到許多關注和研究。Lian等人于2009年首次提出了的LC算法,[1]在LC算法中第一次研究了PRNN問題,對于不確定對象LC算法采用了連續的概率密度函數來表示,該算法采用了數據集中的可能模型,對于數據集的不確定區域劃分為球形區域,當查詢的結果大于該概率閥值則成為RNNs。
Cheema等人于2010年首次提出了CLWZP算法,[2]但該算法僅僅適合用于離散分布情況,并且采用了基于非平凡修建的規則和概率閥值的修剪算法,這樣能夠解決高維空間的不確定修剪不確定和收縮修剪區域的問題,比近似抽樣算法具有更高效和更具有擴展性。
Emrich等人于2010年對MBRs的空間剪枝方法提出了最優的研究方法,而Bernecker等人于2010年對概率近似性排序研究了相關算法,[4]該算法提出了概率剪枝法來加速排除不確定對象的相似。[5]基于這些前提的研究,Bernecker等人于2011深入研究了PNNR查詢,首次提出了概率修剪方法。[6]目前對確定數據集對象上多類型最近鄰反向查詢有一部分相關研究。[7-12]本文針對多個不同類型的不確定數據集對象,提出了MTPNNR查詢的概念,并基于離散型不確定數據集對象模型提出了MTPNNR查詢算法。
2 相關理論
2.1 基本概念
4.2 實驗
本實驗通過與base-MTPNNR算法相比較及逐步調整各輸入參數來驗證MTPNNR算法的有效性。MTPNNR算法與base-MTPNNR算法相比,對于概率提純和過濾的上,采用了分層的概率剪枝,這樣大大節省了計算所有概率特征線路和所有不確定數據集的實例。
圖1比較了MTPNNR算法與base-MTPNNR算法的性能。如圖所示,當FT=1時,其算法相差不大,查詢時間基本相等。圖2比較了基線算法和MTPNNR算法關于Ins查詢性能。
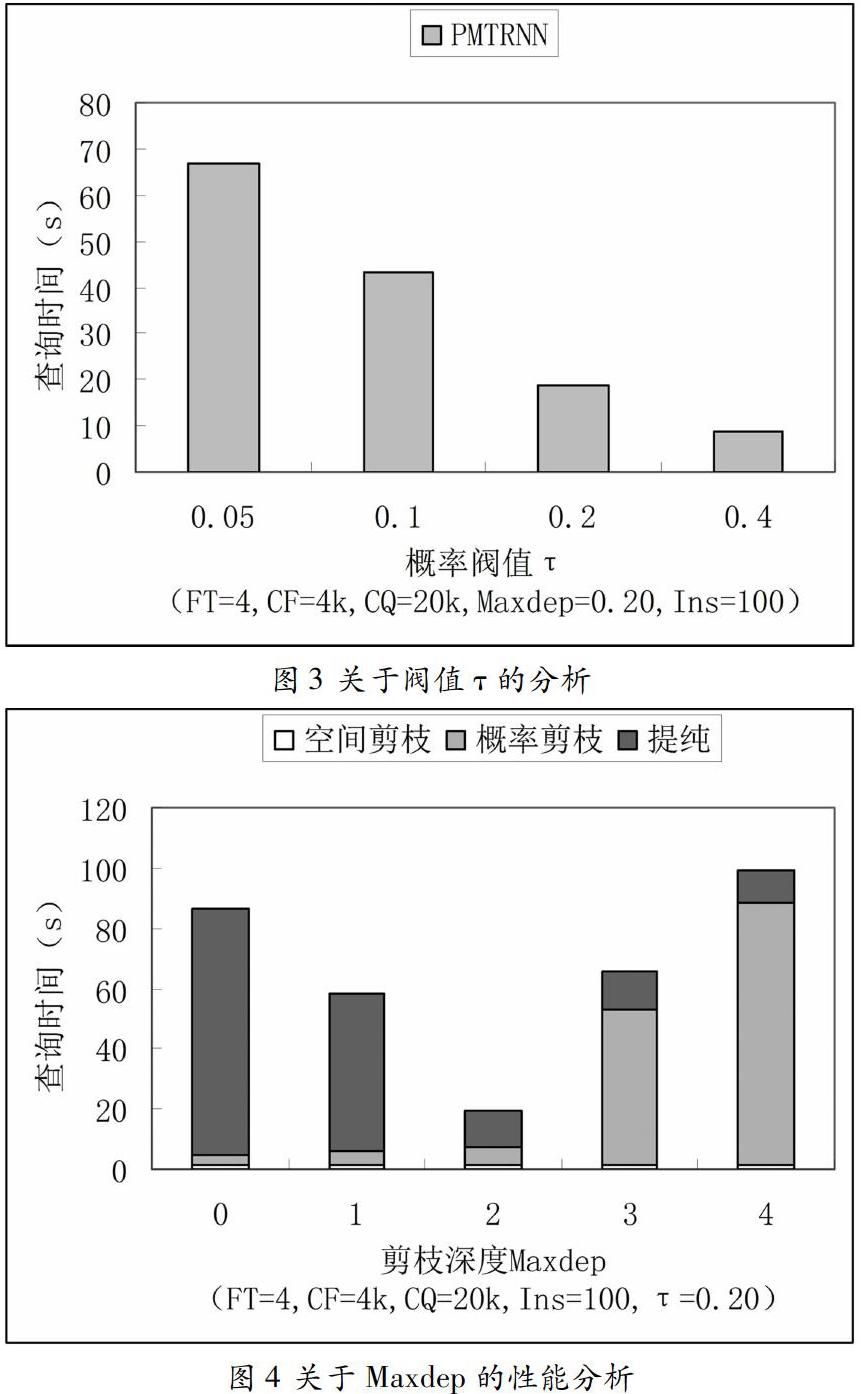
圖3描述了概率閥值對MTPNNR查詢的效率影響。從圖中可以看出MTPNNR的執行時間是隨著τ值的增大而減小。這是由于較大的τ值會使互斥的最小概率1-τ的值減小,那么當MTPNNR概率閥值增大時,其搜索空間對象相應的隨著被修剪的概率1-τ減小而減少,所以在概率剪枝計算時,是很快找到所需的修剪閥值,是的增快了剪枝速度。
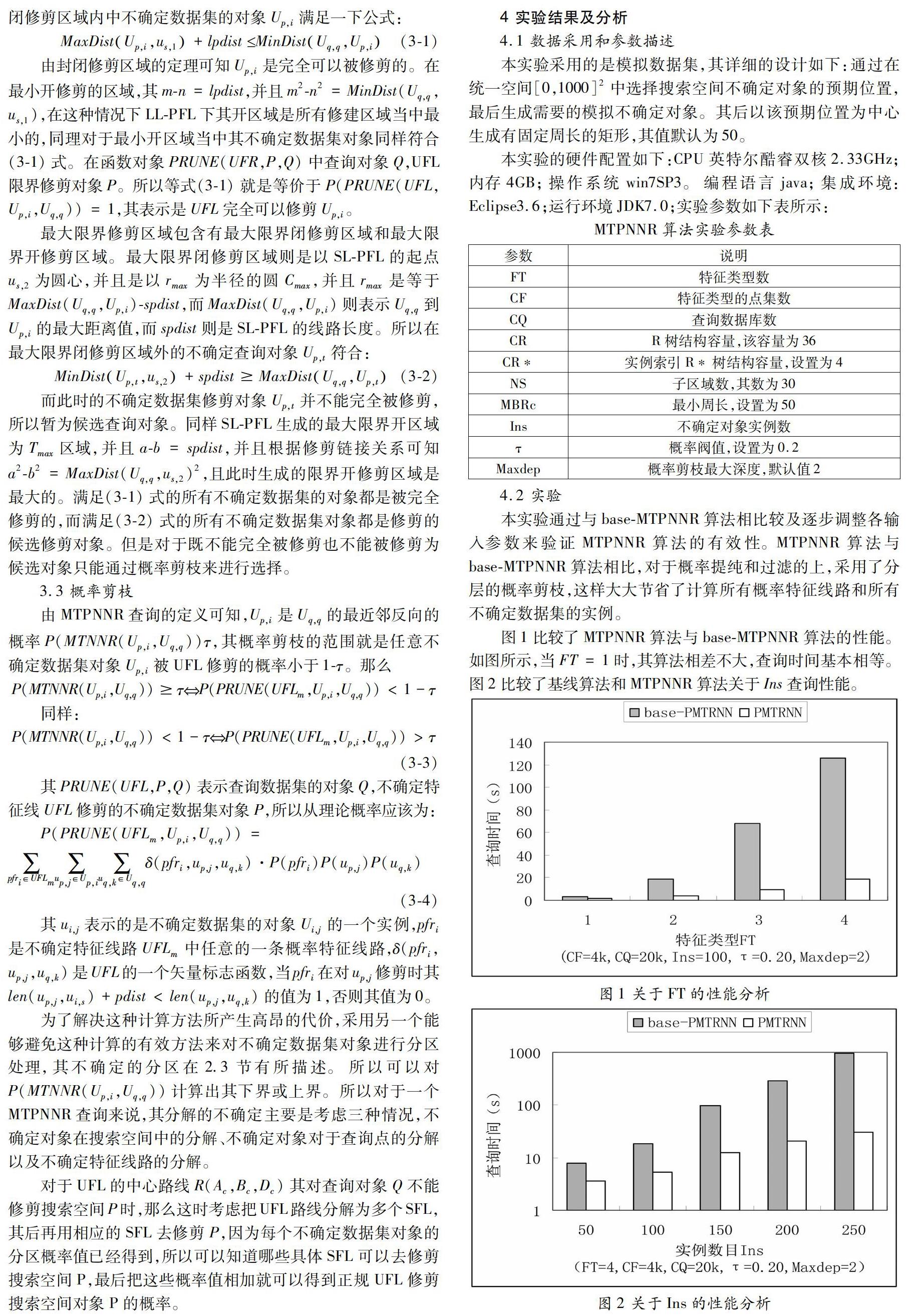
圖4-4是展示了MTPNNR算法對于Maxdep的查詢性能分析的結果,從圖中看到,隨著Maxdep增大,可以明顯的降低提煉步驟的CPU資源消耗。很顯然對于Maxdep來說,提煉步驟是主要的資源瓶頸,這是因為對于較小的Maxdep值,每個在用于概率剪枝的不確定數據集對象的子區域集合是很小的,但是其分區很大。
經過本次實驗可知,MTPNNR算法的查詢性能是與各個輸入參數有直接的聯動關系,并且實驗結果驗證了MTPNNR查詢算法的有效性,并且能夠在較合理的時間段內完成相關查詢和剪枝。
5 結語
本文提出了多類型概率最近鄰反向查詢MTPNNR算法。并且針對MTPNNR查詢的需求,提出了SL-PFL和LL-PFL的特征概率修剪方法,從而整天提高了算法的空間查詢和剪枝效率。其次是運用了限界剪枝方法,分層進行剪枝,最后通過計算概率剪枝的上下界的方法進行概率剪枝,最后通過實驗,并且通過調整輸入參數使得MTPNNR查詢算法達到最優,并且實驗結果驗證了MTPNNR算法的有效性,能為不確定數據集對象上的多類型概率最近鄰反向查詢提供有意義的參考。
參考文獻:
[1]Lian X,Chen L.Efficient processing of probabilistic reverse nearest neighbor queries over uncertain data[J].The VLDB Journal,2009,18(3):787-808.
[2]Cheema M A,Lin X,Wang W,et al.Probabilistic reverse nearest neighbor queries on uncertain data[J].IEEE Transactions on Knowledge and Data Engineering,2010,22(4):550-564.
[3]Emrich T,Kriegel H P,Kroger P,et al.Boosting spatial pruning:On optimal pruning of MBRs[C].Proceedings of the 2010 ACM SIGMOD International Conference on Management of data.New York:ACM Press,2010:39-50.
[4]Bernecker T,Kriegel H P,Mamoulis N,et al.Scalable probabilistic similarity ranking in uncertain databases[C].Proceedings of IEEE Transactions on Knowledge and Data Engineering.[s.l.]:TKDE Press,2010:1234-1246.

