基于兩種預壓縮模型的格萊圈靜密封性能
蔡智媛, 王冰清, 彭旭東, 郭生榮, 孟祥鎧
(1. 浙江工業大學 過程裝備及其再制造教育部工程研究中心, 杭州 310032;2. 中航工業金城南京機電液壓工程研究中心, 南京 211106)
近年來,我國密封行業迅速發展,但也面臨著因高速、高壓和高溫等苛刻工況下引起的密封易泄漏失效.為滿足更高的參數工況條件,延長密封壽命和提高密封可靠性,密封件結構形式也逐步向橡塑組合的形式發展[1].橡塑組合密封也因其具有低摩擦、自潤滑、耐磨損等特性而被廣泛應用于航空航天、建筑、礦山等行業的機械設備中[2].
格萊圈(Glyd-ring)密封是一種典型的橡塑組合密封,一般由一個矩形聚四氟乙烯(PTFE)滑環和一個提供彈性支撐的O型橡膠圈組成,其性能直接關系到液壓系統的運行可靠性和安全壽命[3].目前,關于格萊圈密封的研究已有不少.張付英等[4]系統分析了倒角大小、接觸寬度、活塞桿速度、摩擦系數等參數對密封力學性能的影響;楊忠炯等[5]運用MATLAB/Simulink仿真分析了不同基礎振動參數下間隙的波動規律,并采用Abaqus軟件研究了基礎振動下格萊圈的靜密封性能變化;Heipl等[6]設計了測試高速情況下階梯密封摩擦特性的裝置,比較了不同類型密封件的摩擦特性;王冰清等[7]基于軟彈流理論分析了液壓格萊圈的密封機理,給出了相關操作工況參數對密封性能的影響規律.以上研究成果在一定程度上揭示了格萊圈密封的密封機理,初步明確了相關參數對密封性能的影響;但是,在格萊圈安裝預壓縮過程的有限元模擬中,上述研究為簡化計算量普遍通過活塞桿或活塞的徑向壓縮實現密封圈過盈裝配,這顯然與密封圈實際安裝預壓縮過程表現出的行為存在差異,可能造成仿真預測出現誤差.
在實際安裝過程中,往往是先通過導向套和整形套配合使用,把格萊圈O型橡膠圈沿軸向推進溝槽內,用礦物油加熱PTFE滑環使其脹大,然后通過導向套和整形套配合使用快速將其推入,靜置冷卻等待其恢復原狀,再將活塞軸向推入缸體實現密封件的過盈預壓縮安裝[8].鑒于此,目前國內已有相關學者應用有限元法針對密封圈實際安裝過程的受力情況進行分析,但普遍以單彈性體O型圈為研究對象,有關成果缺乏對橡塑組合密封分析的直接指導意義[9].
本文以格萊圈密封為研究對象,借助ANSYS軟件建立軸對稱二維幾何模型,采用更符合實際的軸向推進預壓縮有限元模型對格萊圈的靜密封性能進行分析,預判密封易失效部位;并與目前普遍采用的徑向壓縮預壓縮有限元模型分析結果進行對比,指出兩者的差異,為格萊圈密封的設計與安裝提供理論指導.
1 計算模型及方法
1.1 幾何模型
具體的格萊圈密封安裝過程如圖1所示.圖 2 所示為目前仿真分析通常采用的徑向壓縮和根據實際安裝預壓縮行為建立的軸向推進兩種預壓縮有限元分析模型(以下分別簡稱為徑向壓縮模型和軸向推進模型)的幾何示意圖.由圖2可知,該幾何結構由PTFE滑環、橡膠O型圈、缸筒和活塞組成.其中,格萊圈結構選自Trelleborg公司的產品RG0519500, O型圈結構尺寸為?15.2 mm×2.62 mm,PTFE滑環結構尺寸為2.9 mm×1.4 mm;采用矩形溝槽,其尺寸嚴格按照GB/T 15242.3-94《液壓缸活塞和活塞桿動密封裝置用同軸密封件安裝溝槽尺寸系列和公差》設計;定義缸筒與PTFE滑環接觸的區域為主密封面.

圖1 格萊圈安裝示意圖Fig.1 The installation schematic of Glyd-ring

圖2 有限元分析用幾何模型Fig.2 Geometric model for finite element analysis
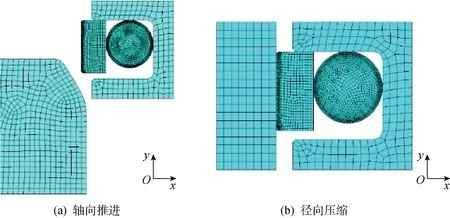
圖3 有限元模型Fig.3 Finite element model
1.2 材料的本構模型
橡膠材料是一種典型的非線性材料,其變形與所受應力表現為高度的非線性.許多學者在大量實驗的基礎上提出了描述該類材料的不同本構模型,如Neo-Hookean、Mooney-Rivlin (M-R)和Klosne-Segal[10].其中M-R模型在中小應變下具有較高的精度,可描述橡膠材料的真實特性且被大量的實驗所驗證[11].本文采用其中較為經典的二項參數模型來描述O型圈的力學行為,表達式為
W=C10(I1-3)+C01(I2-3)
(1)
式中:W為應變勢能函數;I1和I2分別為第1和第2 Green應變不變量;C10和C01分別為M-R模型系數,均為正定常數.本文采用的O型圈材料為聚氨酯,其彈性模量為43 MPa,泊松比為0.499.M-R模型系數分別為:C10=0.402 MPa;C01=1.143 MPa[12].
活塞和缸筒材料均為304不銹鋼,其彈性模量為210 GPa,泊松比為0.3.PTFE材料彈性模量為550 MPa,泊松比為0.4.不失一般性,取密封溝槽與O型圈的摩擦因數為0.25,PTFE滑環與缸筒的摩擦因數為0.1[13].
1.3 有限元模型及邊界條件
有限元分析模型中O型圈和PTFE滑環均選用超彈體平面6節點單元 PLANE183,而合理選擇分析網格的數量,是保證較高計算效率和可靠計算精度的有效手段.探索發現,在保證接觸區域網格足夠密的條件下,當網格數目在(7~15)×104范圍內時能使計算數據誤差小于5%,因此本文在兼顧計算效率和精度的情況下,繪制 75 463 個網格開展分析研究,有限元分析計算所用網格模型如圖3所示.設置滑環與缸筒、滑環與溝槽、滑環與橡膠彈性體、橡膠彈性體與溝槽4個接觸對,接觸方式均為“面-面”接觸,接觸類型為剛-柔接觸,接觸算法采用加強拉格朗日法.
具體的邊界條件如下:所有過程中活塞均施加位移全約束.在安裝過程的仿真模擬中,針對軸向推進模型對缸筒施加y軸正方向位移,直至密封圈達到初始安裝位置;針對徑向壓縮模型對缸筒施加x軸正方向過盈量位移,直至密封圈達到初始安裝.在加壓過程中,對介質側與流體存在潛在接觸可能的密封件表面施加流體壓力載荷,模擬流體壓力施加過程.其中,流體壓力邊界精確解的確定采用逐點搜尋實現.
2 計算結果分析
2.1 安裝過程中格萊圈力學性能

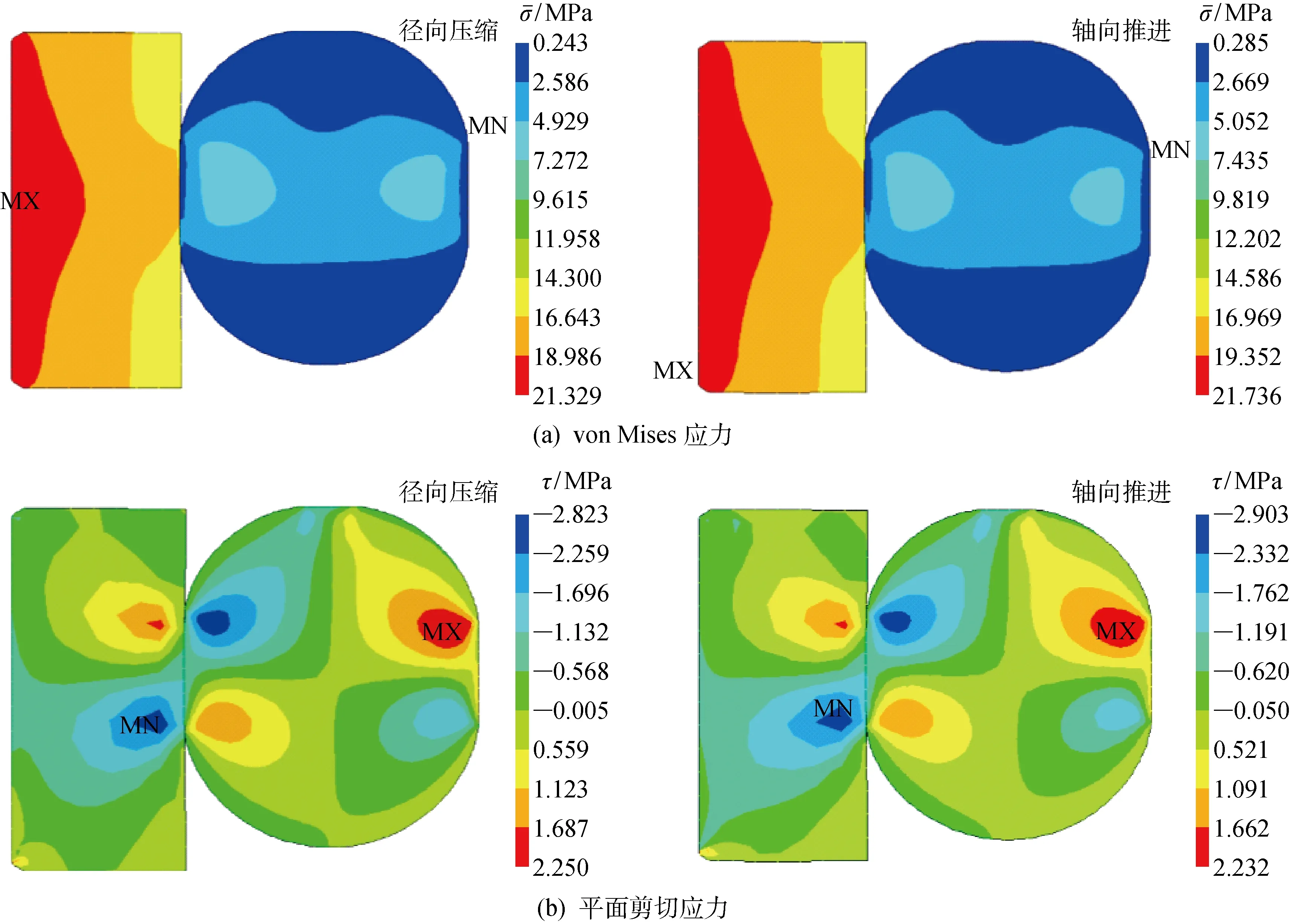
圖4 安裝狀態下的應力云圖Fig.4 Stress nephogram of installation condition
當密封件所受剪切應力超過材料允許的剪切強度時,密封圈會發生剪切撕裂破壞失效.圖4(b)示出了兩種模型下密封圈所受平面剪切應力值的大小及其分布.結果表明,兩種模型預測的O型圈結構的剪切應力分布幾乎一致(最大值相對誤差不到1%),且對整個密封件來說,預測的最大剪切應力的最大值和最小值發生區域基本一致.但對PTFE滑環應力的預測略有差別,這也是由于軸向推進模型中接觸摩擦力的差異造成的(見圖5(a)).

圖5 安裝狀態的接觸應力分布Fig.5 Contact stress distributions of installation condition
圖5(a)和5(b)分別示出了徑向壓縮和軸向推進兩種模型對應的格萊圈密封接觸摩擦力(f)和接觸壓力(p)的分布.一般來說,接觸摩擦力是密封界面存在的阻礙相對運動產生的反向應力,其值在一定程度上反映了密封表面是否存在磨損失效的危險.圖5(a)表明,兩種模型下格萊圈的最大和最小摩擦應力值均發生O型圈表面,這是由于O型圈表面具有相對較大的摩擦因數所致,也從一定程度上反映了O型圈在溝槽內存在滾動或扭曲的風險.對PTFE滑環而言,徑向壓縮模型預測主密封面接觸摩擦應力存在方向的轉變,這顯然區別于實際過程中密封界面的接觸摩擦應力.進一步來看,軸向推進模型中界面靠近流體介質側具有接觸摩擦力突變峰值,說明滑環的該側倒角容易發生磨損失效.圖5(b)表明,當采用軸向推進模型時,在滑環靠近空氣側槽口倒角處出現了接觸壓力峰值,進一步說明該處為密封易發生失效的“潛在”部位.
2.2 壓縮率對靜密封性能的影響
依據文獻[15],確定本文壓縮率ε的研究范圍為8%~20%.圖6所示為介質壓力(pm)為15 MPa時,不同壓縮率下徑向壓縮和軸向推進兩種預壓縮模型預測的最大von Mises應力和主密封面最大接觸壓力的變化情況.可以看出,兩種模型預測密封圈的最大von Mises應力和最大接觸壓力(pmax)均隨壓縮率的增大而增大.
由圖6(a)可見,當壓縮率較小時,兩種模型預測的最大von Mises應力變化均較為平緩,對應最大von Mises應力的位置基本一致,均發生在滑環與空氣側溝槽槽口圓角接觸處.此時采用兩種模型進行靜力學分析均基本合理,但軸向推進模型預測的最大von Mises應力值始終大于徑向壓縮模型的預測值.這是因為活塞與缸筒間存在較大間隙,導致主密封面存在的切向摩擦力使滑環表面產生微小切向變形,造成滑環材料在介質側倒角處“聚集”而形成較大擠壓變形,產生應力集中現象.同時看出,當壓縮率較大時,應力變化加劇,軸向推進模型預測的最大von Mises應力反而小于徑向壓縮模型的預測值,且徑向壓縮模型預測的最大應力位置仍在滑環與空氣側溝槽槽口圓角接觸處并逐漸向滑環與軸接觸的倒角處移動,而軸向推進模型預測的最大應力位置隨軸向推進量增大向內移動,并保持在與筒體接觸的PTFE滑環中部.這是由于摩擦力增大,但間隙減小,軸向推進模型預測主密封面存在的切向摩擦力與方向相反的介質壓力相互作用,使PTFE滑環的切向變形主要集中在主密封面中部,而徑向壓縮模型預測的介質壓力擠壓下,PTFE滑環產生的主密封面的切向摩擦力使滑環表面切向變形小于整體變形,所以使接近空氣側與缸筒接觸的滑環材料變形加大,出現應力集中,導致壓縮率較大時,徑向壓縮模型預測的應力值大于軸向推進模型預測值.因此,在壓縮率較大時,考慮安裝過程的安全性,采用軸向推進模型進行研究設計更為合理.

圖6 壓縮率與兩種模型應力關系曲線及云圖Fig.6 Relation curves and nephograms of compression rates and stresses of two models
由圖6(b)可見,主密封面最大接觸壓力隨壓縮率的增大而增大,且始終滿足密封要求,且與圖 6(a) 所示的最大von Mises應力變化趨勢一致.隨著壓縮率的變化,軸向推進模型的主密封面最大接觸壓力從比徑向壓縮模型的大到比其小,且密封結構的最大接觸壓力分布基本一致,進一步表明在壓縮率較小時,使用兩種模型均可,但徑向壓縮模型更為安全,而壓縮率較大時,采用軸向推進模型進行研究設計更能確保可靠.
2.3 介質壓力對靜密封性能的影響
圖7所示為ε=12%,介質壓力pm分別為0、5、10、15、28和35 MPa時,由徑向壓縮和軸向推進兩種模型預測的格萊圈密封最大von Mises應力以及PTFE滑環主密封面的最大接觸壓力曲線與云圖.
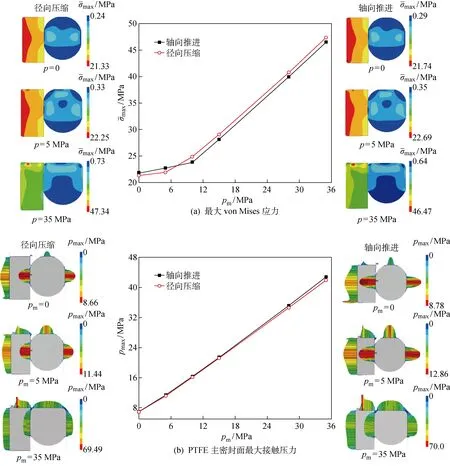
圖7 介質壓力與兩種模型應力關系曲線及云圖Fig.7 Relation curves and nephograms of medium pressures and stresses of two models
由圖7(a)看出,當壓力較低時,隨著壓力的增加,兩種模型預測的最大von Mises應力其變化較為平緩,這歸因于格萊圈的von Mises應力主要由O型圈的初始壓縮決定;隨著壓力繼續增大,最大von Mises應力加速變化,與介質壓力呈現明顯線性關系.最大von Mises應力隨介質壓力的變化規律與壓縮率相似.當介質壓力較低時,軸向推進模型預測的最大von Mises應力大于徑向壓縮模型預測值,且最大von Mises應力的位置從無介質壓力時的介質側PTFE滑環倒角處,到小介質壓力時的與缸筒接觸PTFE滑環主密封面中部,最終穩定在PTFE滑環與空氣側溝槽槽口圓角接觸處;而徑向壓縮模型預測的最大值位置在無介質壓力時為與缸筒接觸PTFE滑環主密封面中部,施加介質壓力后始終處于PTFE滑環與空氣側溝槽槽口圓角接觸處.這是由于溝槽與缸筒間存在較大間隙,軸向移動時,摩擦力作用PTFE滑環主密封面材料產生輕微軸向移動,介質壓力小使PTFE滑環整體變形較小時,無法消減摩擦力的作用,使與缸筒接觸PTFE滑環主密封面中部出現較大von Mises應力.介質壓力增大時,抵消摩擦力的作用,使PTFE滑環整體軸向移動擠入間隙,使PTFE滑環與空氣側溝槽槽口圓角接觸處產生最大應力.但兩種模型的應力值大小基本一致,因此當壓縮率恒定時,針對不同介質壓力進行靜力學研究分析兩種模型均可適用.
由圖7(b)可知,隨著介質壓力的增大,兩種模型的主密封面最大接觸壓力隨之增大,最大接觸壓力始終大于介質壓力,滿足密封要求[4],且兩種模型密封結構的最大接觸壓力的大小及分布基本一致,從而主密封面上的表面接觸摩擦力也基本相等(摩擦因數相等情況下).如前所述,兩種仿真模型所預測的應力分布差異主要是由表面摩擦力引起的,因此在開展靜力學特性分析時,針對定壓縮率、變介質壓力工況的研究,兩種模型均可適用.
3 結論
針對不同介質壓力與壓縮率,對模擬密封圈安裝過程中采用的軸向推進和徑向壓縮兩種預壓縮有限元模型進行了對比研究,通過分析比較發現:
(1) 安裝狀態下,徑向壓縮和軸向推進兩種模型計算所得的密封圈的von Mises應力分布較為類似,但兩種模型對應的最大von Mises應力的位置存在明顯不同.軸向推進模型由于主密封面切向摩擦力的存在,最大值發生在滑環靠近介質側的倒角處,表明該處安裝過程中易發生“畸變”,與實際安裝過程中反饋的問題更為切合.
(2) 當介質壓力恒定、壓縮率變化時,兩種模型模擬所得的應力差異較大.壓縮率較小時,最大von Mises應力位置基本一致,但軸向推進模型的最大von Mises應力始終大于徑向壓縮模型的最大值,因此采用徑向壓縮模型進行分析設計更為安全;壓縮率較大時,應力變化加劇,軸向推進模型的最大von Mises應力反而小于徑向壓縮模型的最大值,且兩種模型的最大值位置存在差異,因此在壓縮率較大時,需考慮安裝過程,采用軸向推進模型進行研究設計更為合理.
(3) 當壓縮率恒定,介質壓力變化時,兩種模型模擬所得的應力差異較小,分析計算所得的各應力的變化規律及分布基本一致.進一步表明兩種模型的應力差異主要由表面摩擦力引起,因此進行靜力學特性分析,針對定壓縮率和變介質壓力的研究,兩種模型均可適用.

