巧添“隱形圓”解決初中“幾何最值與路徑”問題


摘 要:幾何最值與路徑問題能較好地考查同學們的幾何探究與推理能力及數學思想方法的運用。有些立意新穎、構思巧妙的中考題目,將圓隱藏在已知條件里,隱晦地考查圓的有關知識。解題時,需要通過分析探索,發現這些隱圓,做到圖中無圓,心中有圓。
關鍵詞:幾何最值;隱形圓;定邊對定角;定點定長;夾角定位;圓的定義;動點軌跡
初中幾何中的最值問題是指在一定的條件下,求平面幾何圖形中某個確定的量(如線段長度、角度大小、圖形面積)等的最大值或最小值。在近幾年各地中考中,幾何最值與路徑問題屢屢受到命題者關注,一批立意新穎、構造巧妙的新題、活題脫穎而出。此類問題不僅涉及平面幾何的基礎知識,還涉及幾何圖形的性質、平面直角坐標系、方程與不等式、函數知識等,能很好地考查同學們的幾何探究、推理能力及數學思想方法的運用。本文結合筆者的教學實踐與這幾年的中考題談談初中幾何“與動點有關的幾何最值與路徑”問題的求解策略。
一、 幾何最值的理論依據與基本模型
求解幾何最值的基本依據是:①兩點之間線段最短。②垂線段最短。③在三角形中,兩邊之和大于第三邊,兩邊之差小于第三邊。求幾何最值問題的基本方法有:特殊位置與極端位置法;幾何定理(公理)法;數形結合法等。與圓有關的常用模型如下:
模型1:如圖1,當點P是⊙O外一點,直線PO分別交⊙O于點A、B兩點,則線段PA的長是點P到⊙O的最短距離,線段PB的長是點P到⊙O上的點的最長距離。
理由:在過點P另做直線交⊙O于點A′、B′,則有PA=PO-OA=PO-OA′
模型2:如圖2,當點P是⊙O內一點,直線PO分別交⊙O于點A、B,則線段PA的長是點P到⊙O上的點的最短距離,線段PB的是點P到⊙O上的點的最長距離。
理由:在⊙O另取不同于點A、B的點A′、B′,則有PA=OA-OP=OA′-PO
模型3:定邊對定角
已知點A、點B是定點,平面內的動點P滿足∠APB=n°(n為定角),根據“經過不在同一條直線的三個點有且只有一個圓”可知動點P的運動路徑是圓弧。當0°<n<90°時,可知點P的運動軌跡是以AB為弦的一段優弧APB(A、B兩點除外),如圖3;而當180°>n>90°時,可知點P的運動軌跡是以AB為弦的一段劣弧AB(A、B兩點除外),如圖4;而當n=90°時,點P在以AB為直徑的圓弧上,“定邊對直角”是“定邊對定角”的特例,如圖5。
注:這是動點P的運動軌跡僅做出了弦AB一側的情形,由對稱性可知,AB的另一側還存在一條弧滿足條件。
以上的三種模型,屬于單動點問題。在運動過程中動點的運動路徑圓(或圓弧)并不直接給出,此時需要根據條件把“隱圓”勾畫出來,具體來說“隱圓”一般有如下呈現方式:①定點定長;②定弦定角;③圓的定義。如何確定“隱形圓”的圓心與半徑呢?下面結合各地近幾年的中考熱點考題進一步說明如何利用“隱形圓”巧妙解題。
二、 走進中考,提升思維
(一) 定邊對定角:確定動點的位置在確定的圓弧上,再求線段長度的最值
【例1】 (泉州七中2019屆中考模擬試題)如圖6,∠MON=45°,矩形ABCD的頂點A、B分別在OM、ON上運動,若AB=2,BC=1,則OC的最大值是。
分析:如圖7,假設矩形ABCD不動,讓點O運動。作以AB為斜邊的等腰直角三角形△APB,由AB=2,∠APB=90°,知PA=PB=2,此時圓角角∠AOB=45°,所以動點O在⊙P上運動,OP=AP=2。當O、P、C三點共線時,OC有最大值=OP+PC=2+5(由∠PBC=135°,PB=2,BC=1,可求出PC=5)。
點評:本題的解題很有技巧,把動矩形化為動圓,而定點O在圓上,再用圓與三角函數的知識求線段長。
利用“定邊對定角”模型解題的關鍵是:首先要有“動中找靜”求動點的軌跡的意識,在目標動點處看看是否存在定角。若存在,再尋找該定角是否有相對的定邊,一旦兩者都具有,就自然會產生“圓弧型”路徑,然后找其圓心,定其半徑,求其弧長或最值即可。
(二) 圓的定義法:到定點的距離為定長的所有動點在確定的圓上,再解決路徑長度
在初中階段,動點的路徑常見有三類:直線型路徑、圓弧形路徑、來回型路徑。求動點的路徑長的問題,關鍵是先分析路徑的形狀。
1. 直線型路徑
【例2】 (2017江蘇揚州)已知正方形ABCD的邊長是4,點P是AB邊上的一個動點,連結CP,過點P作PC的垂線交AD于點E,以PE為邊作正方形PEFG,頂點G在線段PC上,對角線EG、PF相交于點O。當點P從點A到點B的運動時,求點O經過的路徑長。
分析:(1)法一:如圖8,Rt△APE的外接圓是以斜為PE為直徑的⊙M,連結OM、AM。正方形EFGH中,∠EOP=90°,則有OM=12PE=AM,所以點O一定在△APE的外接圓上。易知∠1=∠2=45°,所以動點O以必在直線AC上運動,再找臨界點可知:點O的起點位置是點A,點O的終止位置是點線段AC的中點,所以點O經過的路徑長=12AC=22。
法二(雙垂直法):如圖9,過O作OH⊥AB于點H,過O作OK⊥AD于點K,易證明△OHP≌△OKE(AAS),所以OH=OK,根據“到角的兩邊距離相等的點在角的角平分線上”,所以OA平分∠BAD,即點O在AC上運動。剩下同法一可求出。
點評:本題中“用夾角定位法”,可知動點O的路徑是直線型。“用夾角定位法”確定動點路徑的一般步驟是:①找定點,一般是目標動點的起點與終點;②連結目標動點和該定點,證明它與某直線的夾角確定;③采用臨界點法,找出動點的起點與終點,求出路徑。
2. 圓弧形路徑
【例3】 (2017年江蘇宿遷)如圖10,在矩形紙片ABCD中,已知AB=1,BC=3,點E在邊CD上移動,連接AE,將多邊形ABCE沿直線AE翻折,得到多邊形AB′C′E,點B、C的對應點分別為點B′、C′。在點E從點C移動到點D的過程中,求點C′運動的路徑長。
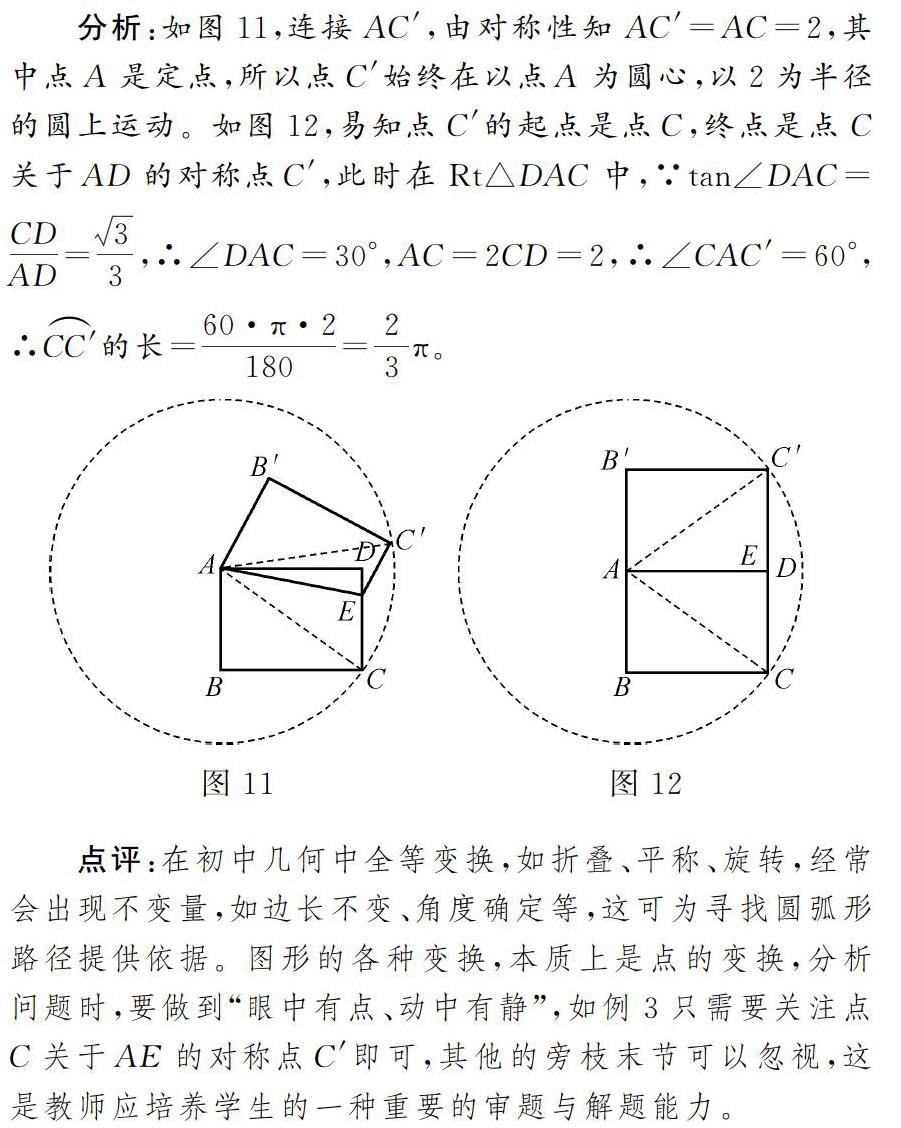
分析:如圖11,連接AC′,由對稱性知AC′=AC=2,其中點A是定點,所以點C′始終在以點A為圓心,以2為半徑的圓上運動。如圖12,易知點C′的起點是點C,終點是點C關于AD的對稱點C′,此時在Rt△DAC中,∵tan∠DAC=CDAD=33,∴∠DAC=30°,AC=2CD=2,∴∠CAC′=60°,∴CC′的長=60·π·2180=23π。
點評:在初中幾何中全等變換,如折疊、平稱、旋轉,經常會出現不變量,如邊長不變、角度確定等,這可為尋找圓弧形路徑提供依據。圖形的各種變換,本質上是點的變換,分析問題時,要做到“眼中有點、動中有靜”,如例3只需要關注點C關于AE的對稱點C′即可,其他的旁枝末節可以忽視,這是教師應培養學生的一種重要的審題與解題能力。
若遇到“來回型路徑”,則需要先定性分析,再定量計算,并且結合解析幾何、消參數的技巧,在高中解析幾何中會系統學習。本文就不詳細舉例說明。
三、 小結與反思
從以上的例題分析中,筆者認為有些數學問題,將圓隱藏在已知條件里,隱晦地考查圓的有關知識。解題時,需要我們通過分析探索,發現這些隱圓,做到圖中無圓,心中有圓,使動點的軌跡一目了然。由于這類問題具有很強的探索性,解題時需要運用動態思維、數形結合、特殊與一般相結合、邏輯推理與合情想象相結合等思想方法。在平時的教學中老師多引導學生善于從復雜的幾何圖形中抓住圖形的本質特征,抽象出常用的數學模型,化繁為簡,化難為易,不斷提升數學綜合思維與解題能力。
參考文獻:
[1]鄒黎明,周敏峰,鄒瑜.巧添“隱圓”求幾何最值[J].中學生數學,2018(12).
[2]段廣猛.廣猛說題——中考數學壓軸題破解之道[M].上海:華東師范大學出版社,2018年7月.
[3]吉宏軍.構造隱形圓,妙求幾何最值——以一道幾何最值問題為例[J].數學教學通訊,2018(29).
作者簡介:
曾立萱,福建省泉州市,福建省泉州七中金山校區。

