變利率下再保險雙方聯合最優再保險-投資策略

崔 永，夏登峰，苑偉杰

(安徽工程大學 數理學院，安徽 蕪湖 241000)

再保險是一種保險形式，它是保險商為了分擔風險而支付一定的保費給再保險商，即保險商購買的保險。而投資能有效地使保險商規劃其盈余來實現股東價值最大化。因此，再保險-投資對保險商很重要。

Lundberg[1]和Cramér[2]最早對風險過程進行了探究,提出的風險過程被稱為C-L(Cramer-Lundberg)模型,該模型奠定了隨機風險模型的基礎。Schmidli[3]研究了在擴散和C-L風險模型下的最優比例再保險問題。夏登峰[4]等考慮在含糊厭惡情形下的比例再保險盈余模型，以股東紅利效用最大化為目標，得到了最優紅利和再保險策略。關于再保險雙方的聯合最優再保險-投資策略問題，黃婭[5]從最大化再保險雙方盈余加權和的效用函數這一角度進行了研究。此外，近年有學者[6-8]研究了隨機利率、通脹環境等情況下基于CEV(Constant Elasticity Of Variance)模型的再保險-投資問題。

再保險策略涉及保險商和再保險商兩個主體，他們之間存在利益平衡。Borch[9]指出保險商的最優再保險策略對再保險商不是最優的。因此，把再保險商的情況考慮進去是必要的。例如Zhao[10]討論了CEV模型下保險商與再保險商共同利益的時間一致的再保險投資策略。Li[11]研究了CEV模型下保險商和再保險商的最優投資問題。Huang[12]研究了保險商和再保險商產品的穩健最優投資和再保險問題。Wang[13-14]研究了CEV模型下具有跳躍擴散風險過程的保險商和再保險商最優投資策略，以及Heston's SV(Heston's Stochastic Volatility)模型下保險商與再保險商之間的博弈。Hu[15]等考慮了跳擴散下保險商和再保險商最優再保險-投資策略。

以上研究均沒有考慮變利率情形，但由于通貨膨脹和貨幣政策的調整等不確定因素存在，考慮變利率是必要的。考慮變利率下保險商和再保險商最優再保險-投資策略問題，分別構造保險商和再保險商的財富過程，財富過程由跳擴散風險模型描述。金融市場由無風險資產和價格服從幾何布朗運動的風險資產組成，利率為確定性函數。同時假設保險商和再保險商是含糊厭惡型。采用動態規劃方法和對偶理論建立HJB方程，解出最優策略。最后通過數值模擬，分析參數對再保險-投資的影響。

1 再保險-投資模型

考慮連續時間金融模型，并假設金融市場是無摩擦成本的，即保險商可以連續交易，且交易中不涉及成本或稅收。設(Ω,F,{Ft}t∈[0,T],P)是一個完備的帶流概率空間，信息流{Ft,0≤t≤T}表示直到時間t為止可以獲得的全部市場信息，T>0表示終端時刻。

1.1 保險商的財富過程

在沒有再保險和投資的情況下，保險商的盈余過程R(t)通過跳擴散模型描述：

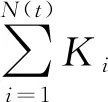
當考慮再保險時，設q1(t)∈[0,1]是再保險比例，當第i次索賠Ki發生時，保險商僅支付q1(t)Ki，再保險商支付(1-q1(t))Ki。再保險保費率通過期望值原理有：c1=(1+η)λμ，其中，再保險安全負荷η>0。于是，在再保險策略q1(t)下，保險商盈余過程為：

假設無風險資產價格S0(t)滿足如下微分方程：

dS0(t)=r(t)S0(t)dt,

其中利率r(t)是確定性函數。

風險資產價格S(t)滿足以下方程：

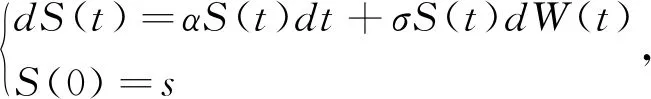
式中，σ>0,W(t)是定義在(Ω,F,{Ft}t∈[0,T],P)上的標準布朗運動，且滿足E[dW1(t)dW(t)]=ρdt，其中ρ∈[-1,1]是相關系數。

1.2 再保險商的財富過程

在比例再保險中,再保險商盈余過程R2(t)滿足:

其中,q2(t)是再保險商選取的再保險比例策略。

2 保險商的最優策略

假設保險商采用指數效用函數:

(1)

式中，γ1>0代表絕對厭惡風險系數，λ1>0和m>0是常數。

對于每一對可容許策略(q1,π1)∈∏1，可以定義值函數:

其中邊際條件H(T,x)=U1(x)。如果值函數H(t,x)和其偏導數Ht，Hx，Hxx在[0,T]×R+是連續的，則H(t,x)滿足HJB方程

(2)

式中，對于任何(t,x)∈[0,T]×R+，其邊際條件H(T,x)=U1(x)。

由一階條件可得：

(3)

把式(3)代入HJB方程式(2)，得到

(4)

式中，H(T,x)=U1(x)。猜測式(4)有以下形式的解：

因為H(t,x)=U1(x)，所以h(T)=0，得到：

Ht=(H(t,x)-λ1)[-γ1xer(t)(T-t)×(rt(t)T-rt(t)t-r(t))-ht(T-t)]，

E[H(t,x-q1(t)K)-H(t,x)]=(H(t,x)-λ1)[MK(γ1q1(t)er(t)(T-t))-1],

(5)

把式(5)代入式(4)，得到:

(6)

其中,

f(q1(t))=λ(H(t,x)-λ1)×[-μγ1(1+η)q1(t)er(t)(T-t)+MK(γ1q1(t)er(t)(T-t))-1]。

(7)

對式(7)關于q1(t)求導，得到:

因此，f(q1(t))是凹的，其最大值q1(t)滿足以下方程:

(8)

引理1 方程(8)有唯一正根ε。

證明令

則

v′(ε)=-E[K2eεK]<0,v″(ε)=-E[K3eεK]<0,

因為v(ε)是遞減的凹函數，并且v(0)=μη>0,因此v(ε)與橫坐標軸交于唯一點。以上說明式(8)有唯一正根ε。

證畢。

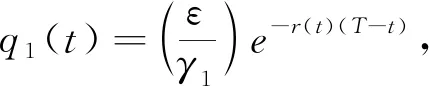
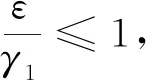
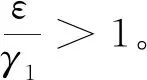
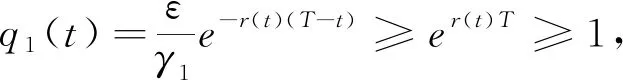
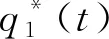
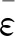
把上式代入式(6)，得到:

(9)

于是隨機控制問題轉化為求解一個關于值函數H(t,x)的偏微分方程。下面將通過Legendre變換運用邊際條件H(T,x)=U1(x)求解方程(9)。

定義2 設H:R→R是一個凸函數。對于z>0，定義Legendre變換:

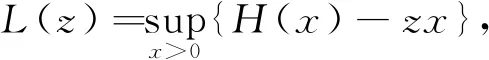
函數L(z)為H(x)的Legendre對偶函數。

為求解方程式(9)，定義以下Legendre變換：

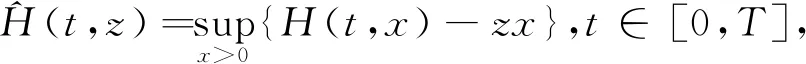
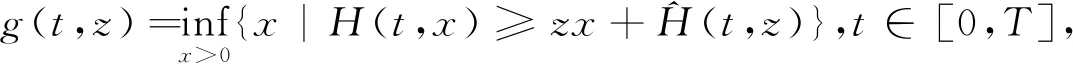
(10)

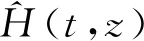
在終端時刻T，有H(T,x)=U1(x)，所以

因此，得到:

(11)

式(11)表明g(T,z)是邊界效用的逆。

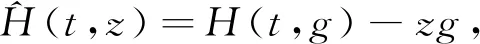
(12)

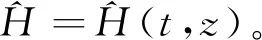
(13)

其中，

式(13)關于z求導，并令ρ2=1，有

(14)

最優投資策略(3)可表示為式(15)：

(15)

解決式(14)的對偶g(t,z)，并將其替換為式(15)以得到最優策略。

由式(1)和式(11)可知,

構造式(14)的解為:

其中，a(T)=1,b(T)=0。于是，

(16)

將式(16)代入式(14)，有

進一步，有

a(t)r(t)-at(t)=0,

把邊際條件a(T)=1，b(T)=0代入，可得:

綜合以上討論，可得以下定理。

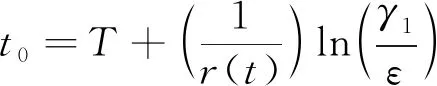
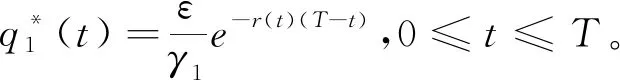
(2)如果γ1≤ε≤γ1er(t)T，最優再保險策略為:

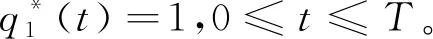
最優投資策略為：

若r(t)為正常數r時，最優投資策略為：

3 再保險商的最優策略

假設再保險商的效用函數如式(17)所示：

(17)

式中，γ2>0代表絕對厭惡風險系數。λ1>0和m>0是常數。

對于每一對可容許策略(q2,π2)∈∏2，可以定義值函數:

式中，邊際條件H(T,y)=U2(y)。相應的HJB方程是:

(18)

式中，邊際條件H(T,y)=U2(y)，值函數H(t,y)的偏導數分別為Ht，Hy，Hyy。

類似于式(8)，對于再保險商，有

其中,

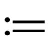
(19)

類似于定理3，得到定理4。

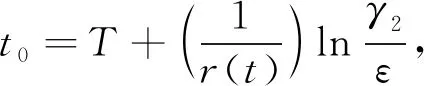
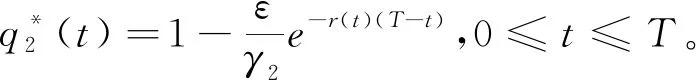
(2)如果γ2≤ε≤γ2er(t)T，最優再保險策略為

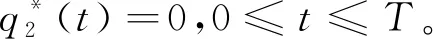
最優投資策略為：

若r(t)為正常數r時，最優投資策略為：

4 數值模擬

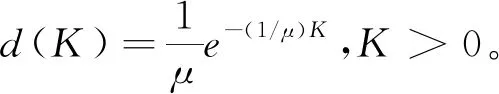
進一步可以得到，

利用Matlab數值模擬，為了方便分析，假設r(t)為正常數r，除特殊說明外，基本參數設置如表1所示。

表1 各項參數

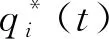
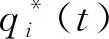
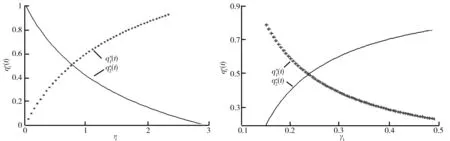
圖1 η對的影響 圖2 γi對的影響

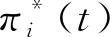
圖3 γi對的影響

此外，當γ1=γ2時，保險商和再保險商的最優再保險策略和為1，反映了保險商和再保險商之間的博弈過程。

5 結論

在研究中同時考慮了保險商和再保險商終端財富效用最大化時，各自的最優再保險-投資策略問題。應用隨機控制理論得出相應的HJB方程，再考慮指數效用最大化情形下的最優再保險-投資策略。對比雙方的最優投資策略，保險商的再保險策略不同于再保險商的策略，最優再保險策略與再保險商的安全負荷和索賠分布有關。當風險模型和風險資產價格存在相關性時，金融市場和保險市場參數都會影響最優投資策略。否則，投資策略僅被金融市場參數和投資者的風險偏好影響。當保險商和再保險商具有相同的絕對回歸風險系數，兩個最優保留比例和為1，說明了保險商和再保險商之間的利益沖突。最后，分析了參數對最優策略的影響并且給出數值模擬及相關經濟學解釋。