中震作用下超限高層結構抗震性能分析
——對長沙福晟金融中心的專例評價

李 峻

(福建六建集團有限公司 福建福州 350014)

0 引言

近年來，隨著施工技術的發展和建筑結構體系的完善，高層甚至超高層建筑的設計、施工不再受到限制，超高層建筑也不斷涌現。而我國許多區域處于地震多發地帶，抗震防災成為結構設計的重要組成部分。超高層建筑由于體型復雜，高度較高，在地震作用下的結構響應也不同于普通建筑[1]。因此，通過對超高層建筑進行抗震性能分析來優化設計方案，對提高建筑抗震等級和降低地震災害具有較大工程應用價值。

我國能在復雜超高層建筑結構領域取得高速發展離不開科研工作者的研究成果。呂西林，等[2-3]采用Perform 3D建立某高層結構數值模型，通過彈性分析其抗震性能，與規范對比分析，結果表明該建筑在罕遇地震作用下依然滿足性能要求。郝嶸，等[4]利用SATWE對某超限高層框剪結構進行分析，通過調整剪重比等參數來優化設計，對優化后的設計方案進行罕遇地震作用下的彈塑性分析，結果表明優化后結構能滿足“大震不倒”的設計要求。陳濤，等[5]對兩類剪力墻進行建模分析，通過對比分析延性性能，為超限高層剪力墻的設計提供了參考依據。張崢，等[6]則從概念設計、結構體系設計和超限分析等方面對連體結構進行抗震分析，為工程應用提供改進措施。生永栓，等[7]通過對某超限高層分析表明，要滿足規范中提出的“三水準”抗震設計目標，在實際工程建設時需要提高抗震設計標準和加強構造措施要求。蘭和義，等[8]利用ETABS及SATWE建立長沙福晟金融中心的有限元模型，通過“中震不屈服”分析，對結構設計方案進行性能評價，給出相關建議措施。

綜上所述，由于超高限建筑結構較為復雜，在不同抗震設防水準下，其地震響應規律不明確，因此有必要對超高層建筑設計方案進行抗震專項分析，以此提高結構抗震性能。本文以長沙福晟金融中心超高限建筑為研究背景，對其框架柱、連梁、剪力墻等進行中震彈性分析或不屈服分析，評價結構抗震性能。

1 工程概況

長沙福晟金融中心是超高層商務辦公大廈，地下3層，地上46層，結構總高度約204m，1F～5F為商業裙樓，層高均為5.4m，6F以上為商務寫字樓，層高均為4.3m。整棟大樓設置了3個避難層，分別設置于16F、29F和42F，建筑周邊設置了高度為26m的裙房，裙房共5層，層高與塔樓一致。同時，樓底設置了3層地下停車庫。考慮結構抗震設防要求，在塔樓與裙房之間設置了防震縫，將塔樓與裙房從結構上形成獨立單元。

地下室和商業裙樓采用混凝土框架結構，塔樓及塔樓區域地下室采用型鋼混凝土柱-鋼筋混凝土核心筒混合結構，混凝土強度等級1F～5F的C60，逐漸過渡到42F～46F的C30。連梁高度從600mm～1000mm不等，墻厚從底層的1100mm～頂層的300mm不等。結構平面布置如圖1所示。

圖1 結構平面布置示意圖

2 有限元模型

根據房建結構特點，數值模型中梁、柱均采用框架單元模擬，可分析構件的彎剪扭作用；剪力墻和樓板利用殼單元模擬，介于板單元和膜單元的計算原理中間，這樣可以考慮構件平面內和平面外的剛度，符合構件實際受力。由于回填土作用，地下室整體可按固結處理，固定端設于地下室頂板位置。利用SATWE軟件建立三維空間模型如圖2所示。

圖2 三維有限元模型

3 抗震設防性能目標

對于不同建筑進行抗震性能化設計，具有較強的針對性，根據工程設計需要，可以是整個結構的性能設計，也可以是局部或關鍵構件的設計。性能化設計綜合考慮了結構承載力和變形能力，根據性能分析結果運用相應措施達到性能目標，以此提高建筑的抗震性能。

根據《高層建筑結構設計規范》第3.11.1～3.11.2條的規定，抗震設防性能目標分為A～D四個等級，抗震性能分為1～5五個水準。根據該工程項目的抗震設防類別、設防烈度和場地條件等因素，確定該建筑抗震性能目標為C級，相應的性能水準如表1所示。

表1 結構抗震性能目標

4 設計地震參數選擇

設計采用抗震規范與安評報告提供的設計基準期為50年(設防概率10%)的場地地面設計地震動參數及曲線。規范及安評報告地震動參數見表2。

表2 抗規及安評報告地震動參數

工程場地設計地震動加速度反應譜由公式(1)確定：

(1)

且βmax=2.5，地震系數Ks=0.1164，αmax=Ksβmax，阻尼比ζ=0.05，γ=1.0。

安評報告中震反應譜與規范對應中震反應譜、小震反應譜如圖3所示。

圖3 小震、中震規范譜及中震場地譜對比

經計算，采用中震規范譜計算基底剪力大于采用安評譜所得基底剪力，所以取中震規范反應譜作為設計依據來定義中震工況。

5 中震作用下結構抗震性能分析

在中震作用下進行結構抗震性能分析，主要目的是驗算結構整體剛度和重要構件的承載力，包括框架柱、剪力墻、框架梁、連梁，以及耗能支撐等。再根據小震設計下得到的實際配筋計算各主要構件的承載力，與中震下的效應組合進行比較，并進行屈服判別。對產生屈服的構件調整結構構件配筋及采取相應加強構造措施，使之滿足預定的性能水準。

5.1 構件承載力驗算方法

根據性能目標，針對第二水準(中震可修)下的中震組合效應進行構件承載力驗算，目前較為常見的技術手段有兩種：一是“中震彈性”分析，即在中震作用下保證結構的承載力在彈性范圍，計算過程中不考慮地震內力調整系數，其他基本同抗震設計的第一階段(小震彈性)。采用與小震時相同的作用分項系數、材料分項系數和抗震承載力調整系數，材料強度取設計值，不考慮風荷載參與組合，組合見表3。截面承載力驗算表達式見式(2)。

表3 地震作用及荷載效應組合

(2)

式中：γRE為承載力抗震調整系數，Rd為構件承載力設計值。

第二種是“中震不屈服”分析，即采用振型分解反應譜法計算地震效應，不考慮內力的調整，荷載以及地震作用分項系數均取1.0。截面驗算過程使用材料強度標準值，對抗震承載力不作調整，同時且不考慮風荷載參與組合，見表4。

表4 地震作用及荷載效應組合

對于本文研究工程中的型鋼混凝土柱和鋼筋混凝土柱、剪力墻、框架梁和連梁采用中震不屈服分析，對底部通高墻和柱的抗剪驗算則采用中震彈性分析。

5.2 主要構件中震不屈服分析

根據擬定的抗震設防性能目標，該項目采用“中震不屈服”的設計方法對構件進行分析，中震截面承載力驗算表達式見式(3)。

(3)

式中：Sk即為荷載效應標準組合值；Rk為結構構件的抗力。

驗算的效應組合和驗算表達式前文已表述，由于剪力墻、框架柱等重要構件的內力構成不同，截面抗力計算方法也不相同。如：對型鋼混凝土柱和普通鋼筋混凝土柱，采用N-M-M包絡面與內力組合效應進行對比分析，以此判斷構件是否屈服。對剪力墻而言，通過N-M包絡線與內力組合效應對比分析，確定剪力墻的屈服情況。

5.2.1型鋼混凝土柱和鋼筋混凝土柱

對單向壓彎柱而言，判斷截面屈服的主要依據是壓彎承載力的包絡線。在實際工程中，由于地震作用方向的不確定性，型鋼混凝土和普通鋼筋混凝土柱均屬于雙向壓彎構件，柱截面的壓彎承載力為雙向偏壓下的承載力，此時包絡線擴展為空間的包絡面，即洋蔥頭形狀的N-M-M曲面。判斷柱截面屈服的依據是組合后的效應點與N-M-M包絡面之間的位置關系，若效應點在包絡面內部，則說明柱截面不屈服；否則認為受壓柱進入了塑性狀態。

為更準確描述受壓型鋼柱和普通混凝土柱的抗震力學性能，利用富余度來描述截面負荷情況。富余度通過組合效應點與N-M-M包絡面表面的最小距離來描述；或通過調整組合效應中的地震作用效應比例直到組合效應點達到包絡面的表面來判斷。兩種方法各有優勢，前面一種方法較為直觀，但受繪圖單位和質量限制，且在結構自重較大的情況下，地震組合效應會被削弱甚至掩蓋。第二種方法即直接揭露地震作用下截面的富余度，但會受到內力路徑的影響。根據已有研究表明，在中震作用下采用分解振型反應譜法，采用第二種方法能更準確描述受彎承載力富余度，剪力以利用率來表示。

由于篇幅所限，文中僅列出了第1層KZ1和KZ2的計算結果，如圖4～圖5所示。

圖4 第1層KZ1的N-M-M包絡面與組合效應點

圖5 第1層KZ2的N-M-M包絡面與組合效應點

由計算可得，一層KZ1受彎富余系數最小值為3.52；受剪利用率最大值為0.024；一層KZ2受彎富余系數最小值為4.16；受剪利用率最大值為0.022。綜合所有分析結果可知，型鋼柱的安全儲備比較高，角柱的富余系數比中柱略小，中震工況下，均未出現受拉情況，各層框架柱能夠保證抗彎及抗剪均不發生屈服，說明構件存在較大的富余度。

5.2.2鋼筋混凝土剪力墻

對超高層建筑核心筒承載能力的驗算一直是個技術難題，目前的做法主要是將核心筒的剪力墻拆解驗算。剪力墻屬于單向壓彎構件，因此，采用N-M包絡線進行驗算。同樣采用截面受彎富余系數和受剪利用率來判斷剪力墻的受力狀態。圖6～圖8為典型樓層剪力墻N-M(軸力-面內彎矩)相關曲線。

圖6 第1層W1剪力墻N-M相關曲線

圖7 第1層W2剪力墻N-M相關曲線

圖8 第1層W3剪力墻N-M相關曲線

由計算可知，第1層W1主要受力方向的受彎富余系數最小值為1.626，受剪利用率最大值為0.365；第1層W2的受彎富余系數最小值為1.094，受剪利用率最大值為0.759；第1層W3的受彎富余系數最小值為1.406，受剪利用率最大值為0.569。

基于限幅機構的功能需求、性能指標及作業載荷，筆者設計了一種鎖合隨動式限幅機構，該機構的結構組成及工作流程如圖4所示。

綜合計算結果來看，中震工況下墻體均未出現拉力，按小震配筋的首層極個別墻體的受彎接近屈服，基本達到屈服的極限，可相應調整加大豎向配筋增加結構的安全儲備；剪力墻的受彎富余系數隨樓層數上升逐漸增大，墻體抗彎富余量相對較大，抗剪安全系數相對較高。

綜上所述，對底部加強區樓層接近屈服的墻體采取適當增大配筋的加強處理措施，可增加結構整體的安全儲備，更好地抵抗地震作用，從而保證結構的整體安全。

5.2.3框架梁和連梁

根據框架梁和連梁的受力特點，其屈服彎矩和剪力主要由截面尺寸、材料強度和配筋率確定。此處采用承載力利用率來判定框架梁的屈服狀況。利用率即為中震作用下的荷載效應與其小震作用下配筋截面的相應承載力比值。例如：框架梁的受彎、受剪截面承載力利用率，定義為框梁截面中震作用下的彎矩、剪力與其小震作用下的實配鋼筋截面的受彎、受剪承載力的比值。以此來衡量框梁受彎及受剪方面的抗震性能。由于篇幅所限，本文僅給出部分分析結果，見表5～表6。

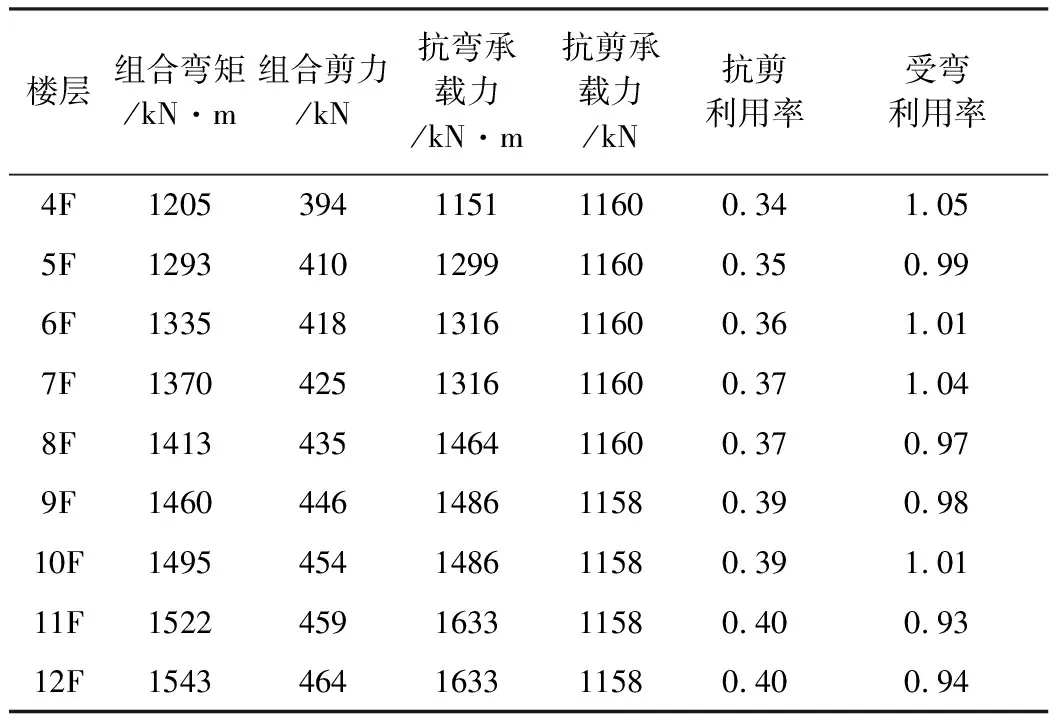
表5 KL2承載能力計算結果

表6 LL2承載能力計算結果

經分析表明，在中震作用下，僅四層、六層、七層和十層(利用率分別為1.05、1.01、1.04和1.01)的KL2出現屈服，其余框梁滿足要求。所有框梁的受剪承載力利用率均不超過55%，絕大多數位于30%～40%之間，存在較大富余，均能滿足預定抗震性能目標。

在中震作用下，僅四十四層LL2連梁(抗彎承載利用率為1.01)出現屈服；但抗剪承載力利用率均不超過100%，絕大多數位于70%～80%之間，存在一定富裕，均能滿足預定抗震性能目標。

5.3 底部通高墻、柱抗剪中震彈性分析

根據抗震設防性能目標，采用“中震彈性”的設計方法對底部通高墻、柱構件進行分析。鋼骨混凝土柱的受剪承載力則采用《鋼骨混凝土結構設計規程》和《建筑抗震鑒定標準》計算，兩者取小值。公式分別為式(4)和式(5)。

(4)

(5)

(6)

按“中震彈性”設計方法分析，典型柱、墻的具體計算結果見表7。

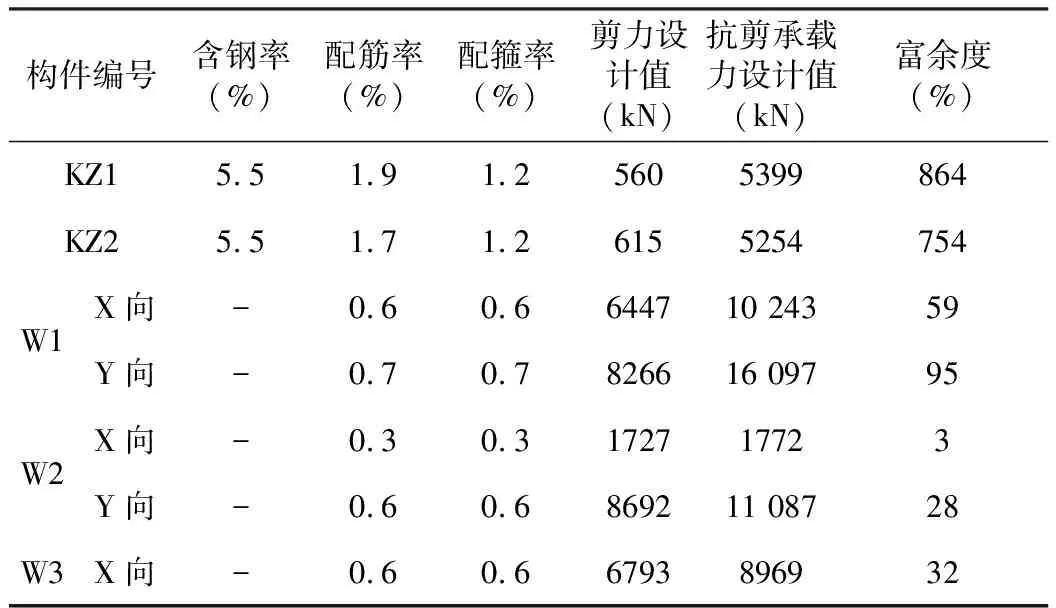
表7 典型柱和墻計算結果

以上結果表明，在中震作用下，底部通高墻、柱均滿足抗剪彈性設計的性能化設計要求。

6 結論

(1)通過中震不屈服分析和判斷可以清楚地看到，豎向構件基本保持著良好的彈性性能。而水平構件中框架梁在考慮樓板增強作用的情況下，有少數構件出現抗彎屈服，其余框架梁基本能保證不屈服。作為主要耗能構件的連梁在地震作用下出現少量受彎屈服，但不嚴重，而抗剪性能仍處于彈性階段，可滿足中震不屈服的要求。

(2)本結構在設計上保證了中震不屈服概念的具體落實，實現了中震可修的性能水準。同時，在中震作用下，連梁先于框架梁屈服，而后剪力墻的塑性鉸區出現屈服，整個過程中框架柱未出現屈服，這與抗震設防二道放線的基本要求相符。

(3)在中震作用下，對底部通高墻、柱進行彈性分析，結果表明，其受彎受剪性能均滿足彈性設計的性能化設計要求。