含優(yōu)先級約束的旅行商問題研究*
□ 張思龍
(上海交通大學(xué) 中美物流研究院,上海 200030)
旅行商問題(TSP)廣泛存在于物流服務(wù)、交通運(yùn)輸、生產(chǎn)制造等應(yīng)用場景中,高效的求解方法有助于減小操作成本、提升服務(wù)效率。很多學(xué)者致力于研究這一問題的精確算法和近似解法,在這方面的杰出貢獻(xiàn)有Lawler等和Gutin等。如果實際問題存在優(yōu)先級約束,此時問題變?yōu)楹瑑?yōu)先級約束的旅行商問題(TSP-PC)。TSP是TSP-PC的一種特殊情況,因此TSP-PC屬于NP-hard問題。
Mingozzi等在考慮含時間窗以及優(yōu)先級約束的TSP時,提出了相應(yīng)的動態(tài)規(guī)劃算法,并采用定界函數(shù)去減小狀態(tài)空間的規(guī)模。Moon等采用遺傳算法求解TSP-PC時,使用拓?fù)渑判蛞约耙环N新的交叉算子來增加解的多樣性。Deineko等和Burkard等研究了某些關(guān)于TSP的變種。
雖然已經(jīng)有不少學(xué)者獲得了豐富的研究成果和經(jīng)驗,由于問題的復(fù)雜性,求解大規(guī)模問題的精確解仍然有著不小的挑戰(zhàn)。為了更好的解決該問題,本文先給出該問題的數(shù)學(xué)模型,然后提出動態(tài)規(guī)劃精確解法,最后進(jìn)行相關(guān)的數(shù)值實驗。
1 問題描述與數(shù)學(xué)模型
1.1 問題描述

TSP-PC的目標(biāo)在于找到一條滿足以下兩個條件的最短的路徑:①該路徑經(jīng)過圖中所有結(jié)點(diǎn)剛好一次;②優(yōu)先級較高的結(jié)點(diǎn)必須先于優(yōu)先級較低的結(jié)點(diǎn)被訪問,即訪問優(yōu)先級較低的結(jié)點(diǎn)之前,必須保證優(yōu)先級比它高的結(jié)點(diǎn)都已經(jīng)被該路徑訪問。
需要注意的是,兩個結(jié)點(diǎn)i和j之間的優(yōu)先級關(guān)系有三種:①i的優(yōu)先級高于j,此時在訪問j之前必須確保i已經(jīng)被訪問;②i的優(yōu)先級低于j,此時在訪問i之前必須確保j已經(jīng)被訪問;③i的優(yōu)先級和j的優(yōu)先級相等,此時不對i和j之間的相對次序作出要求。
為了進(jìn)一步闡明問題,有必要使用算例做出形象解釋。表1是圖中5個結(jié)點(diǎn)的之間的距離矩陣,表2是優(yōu)先級關(guān)系表,可以轉(zhuǎn)化為圖1所示的優(yōu)先級拓?fù)鋱D。路徑{e13,e32,e24}沒有訪問到所有結(jié)點(diǎn),路徑{e13,e32,e24,e42,e25}把結(jié)點(diǎn)2訪問了2次,路徑{e12,e23,e34,e45}違反了結(jié)點(diǎn)2和結(jié)點(diǎn)3之間的優(yōu)先級約束,所以它們都不是可行的路徑。路徑{e13,e32,e24,e45}雖然可行,但是它的長度為18,顯然過大。實際上,該算例的最優(yōu)解是路徑{e34,e41,e12,e25},長度為13。

表1 距離矩陣表

表2 優(yōu)先級關(guān)系表

圖1 優(yōu)先級拓?fù)鋱D
1.2 數(shù)學(xué)模型
建立數(shù)學(xué)模型可以使定義變得更加精準(zhǔn),描述變得更加清晰和嚴(yán)密。為此我們首先介紹它所涉及到的集合、參數(shù)、決策變量,然后建立一個整數(shù)線性規(guī)劃模型。
1.2.1 下標(biāo)和集合
0:虛擬的起始結(jié)點(diǎn)和虛擬的終止結(jié)點(diǎn);
V:V={1,2,…,N}是圖中結(jié)點(diǎn)的集合;
V0:包含虛擬起止點(diǎn)的結(jié)點(diǎn)的集合,V0=V=V∪{0};
i,j:結(jié)點(diǎn)的下標(biāo);
Pi:優(yōu)先級低于結(jié)點(diǎn)的結(jié)點(diǎn)的集合。
1.2.2 參數(shù)
N:圖中結(jié)點(diǎn)的數(shù)量;
dij:弧eij的長度。
1.2.3 決策變量
xij:二元變量,當(dāng)且僅當(dāng)路徑經(jīng)過弧eij時取值為1,否則取值為0;
yi:整數(shù)變量,取值范圍是{1,2,…,N},代表結(jié)點(diǎn)i在路徑中的次序。
1.2.4 整數(shù)線性規(guī)劃模型
(1)
(2)
(3)
yj-yi>(xij-1)N,i∈V0,j∈V:i≠j
(4)
yi (5) y0=0 (6) 1≤yi≤N,integer,i∈V (7) xij∈{0,1},i∈V0,j∈V0:i≠j (8) 式(1)是目標(biāo)函數(shù),表示最小化路徑的長度。式(2)和式(3)是流平衡約束,要求每個結(jié)點(diǎn)的入度和出度均為1,以保證每個結(jié)點(diǎn)剛好被訪問一次。式(4)是為了消除子回路。優(yōu)先級約束體現(xiàn)在式(5)中,確保優(yōu)先級較高的結(jié)點(diǎn)一定先被訪問。式(6)-(8)表明決策變量的類型和取值范圍。 動態(tài)規(guī)劃通過逐步遞推最優(yōu)子結(jié)構(gòu)得到最終的最優(yōu)解,而且能夠消除冗余的中間狀態(tài),可以非常高效地求解TSP-PC問題。為了闡述求解該問題的動態(tài)規(guī)劃算法,本節(jié)內(nèi)容首先定義若干符號和算子,然后給出狀態(tài)轉(zhuǎn)移方程,最后描述算法流程。 應(yīng)該注意到,如前述算例所示,輸入的數(shù)據(jù)Pi只是包含了直接的優(yōu)先級關(guān)系,間接的優(yōu)先級關(guān)系并未被考慮。例如,由P3={2,4},P4={5}得知,結(jié)點(diǎn)3的優(yōu)先級比結(jié)點(diǎn)5高。在紛繁復(fù)雜的大規(guī)模情況下,要想憑肉眼觀察出全面的優(yōu)先級關(guān)系并非易事,因此有必要使用如下的GET_PC算法來達(dá)到上述目的。 GET_PC算法 輸入:優(yōu)先級關(guān)系表Pi,i∈V 輸出:后序集Ai,i∈V,先序集Bi,i∈V,無序集Ci,i∈V 步驟1:初始化Ai←Bi←Ci←?,i∈V,初始化矩陣M:若j∈Pi,則Mij←1;否則Mij←+∞ 步驟2:對矩陣M運(yùn)行弗洛伊德(Floyd)算法 步驟3:對于i∈V,j∈V,i≠j,執(zhí)行:若Mij 步驟4:輸出Ai,Bi,Ci,i∈V算法結(jié)束 運(yùn)行GET_PC算法產(chǎn)生的三種集合的含義分別如下:對于?j∈Ai,i∈V而言,結(jié)點(diǎn)的優(yōu)先級(直接或者間接)高于結(jié)點(diǎn)j,在訪問結(jié)點(diǎn)j之前必須確保結(jié)點(diǎn)i已經(jīng)被訪問;對于?j∈Bi,i∈V而言,結(jié)點(diǎn)的優(yōu)先級低于結(jié)點(diǎn)j,在結(jié)點(diǎn)j被訪問之后才允許訪問結(jié)點(diǎn)i;對于?j∈Ci,i∈V而言,結(jié)點(diǎn)i和結(jié)點(diǎn)j的優(yōu)先級相等,先訪問哪一個都可以。此外,這三個集合互斥,而且它們的并集等于V{i},即有|Ai|+|Bi|+|Ci|=N-1和Ai∪Bi∪Ci∪{i}=V。 下面進(jìn)一步定義一些符號: H:H是一個結(jié)點(diǎn)的集合,且其中所有結(jié)點(diǎn)的優(yōu)先級相等,即對于?i,j∈H,有j∈Ci; s:s={H,i},i∈H是一個狀態(tài),它對應(yīng)著一類路徑,該類路徑訪問過的結(jié)點(diǎn)集合是W(H),且最后訪問的結(jié)點(diǎn)是i; Q(s):Q(s)={j:j∈VW(H),?j2∈VW(H),j2?Bj}是結(jié)點(diǎn)集合,它們尚未被s所對應(yīng)的路徑訪問,且在剩下的結(jié)點(diǎn)當(dāng)中,沒有任何一個結(jié)點(diǎn)的優(yōu)先級高于它們; R(s):表示狀態(tài)s所對應(yīng)的最短路徑; St:St={{H,i}:|W(H)|=t,i∈V},t∈{1,2,…,N}是一類狀態(tài)的集合,這類狀態(tài)所對應(yīng)的路徑訪問過的結(jié)點(diǎn)數(shù)量為t; F(s):目標(biāo)函數(shù),表示狀態(tài)s所對應(yīng)最短路徑的長度;若{H,i}?St,t=|W(H)|,則F({H,i})=+∞。 有了上述定義之后,現(xiàn)在給出狀態(tài)轉(zhuǎn)移條件: j∈Q({H,i}),H′=H∪{j}Bj,F({H,i})+dij (9) 上式對結(jié)點(diǎn)j做了明確要求,且指出了H′的形式:它等于原有集合H并入結(jié)點(diǎn)j之后,再減去所有優(yōu)先級比j高的結(jié)點(diǎn)。另外,只允許發(fā)生讓路徑的長度變得更短的狀態(tài)轉(zhuǎn)移。在式(9)被滿足的情況下,狀態(tài)轉(zhuǎn)移如下進(jìn)行: F({H′,j})=F({H,i})+dij,R({H′,j})=R({H,i})∪{eij} (10) 動態(tài)規(guī)劃算法的另一關(guān)鍵部分是邊界條件: F(?)=0,R(?)=? (11) 具備以上鋪墊之后,現(xiàn)在介紹求解TSP-PC的動態(tài)規(guī)劃精確算法。 DP_TSP_PC算法 輸入:各結(jié)點(diǎn)之間的距離dij,i∈V,j∈V,i≠j,優(yōu)先級關(guān)系表Pi,i∈V 輸出:TSP-PC問題的最優(yōu)解(長度d以及路徑r) 步驟1:運(yùn)行GET_PC算法,得到Ai,Bi,Ci,i∈V 步驟2:初始化:t←1,S0←{?},S1←S2←…←SN←? 步驟3:對于?{H,i}∈St-1,?j∈Q({H,i}),若狀態(tài)轉(zhuǎn)移條件式(9)被滿足,則按照式(10)進(jìn)行狀態(tài)轉(zhuǎn)移,且St←St∪{{H′,j}} 步驟4:若t=N,轉(zhuǎn)到步驟5;否則t←t+1,轉(zhuǎn)到步驟3 介紹數(shù)值實驗的內(nèi)容之前,需要再引入一個符號K,它代表著H中所包含結(jié)點(diǎn)的數(shù)量的上限|H|max。實際上,K的值由優(yōu)先級關(guān)系中的Ci,i∈V唯一確定。這是因為H中各個結(jié)點(diǎn)的優(yōu)先級相等,即?j1,j2∈H,j1≠j2,一定有j1∈Cj2(j2∈Cj1也會自然成立)。 本文實驗使用C++語言編寫的程序,在酷睿四核I7-7700HQ(2.80GHz)和16GB內(nèi)存的計算機(jī)上,求解15個不同規(guī)模的隨機(jī)算例來驗證算法的效率。如表3所示,值、值越大,算例越復(fù)雜。 K值較小的時候求解速度很快,程序能在數(shù)秒內(nèi)給出最優(yōu)解。即使N=100,K=15的時候,最優(yōu)解也能在6分鐘以內(nèi)求得。另外,可以看出當(dāng)N值不變時,K值的增長導(dǎo)致求解時間增長的幅度特別大,遠(yuǎn)比當(dāng)K值不變時單純增大N值帶來的影響強(qiáng)烈,這說明當(dāng)K值不是特別大的時候,K值對復(fù)雜度的影響比網(wǎng)絡(luò)中結(jié)點(diǎn)總數(shù)N值的影響要大。 表3 不同規(guī)模算例所耗費(fèi)的時間 (單位:秒) 本文研究了含優(yōu)先級約束的旅行商問題(TSP-PC)的模型和算法,并對算法做了相關(guān)分析和數(shù)值實驗。在此過程中,建立了整數(shù)線性規(guī)劃模型,但是由于該問題屬于NP-hard問題,所以直接使用求解器求解模型是不夠高效的,為此本文提出了相應(yīng)的狀態(tài)表示方法及動態(tài)規(guī)劃算法。通過數(shù)值實驗證明了該算法的高效性,多達(dá)100個結(jié)點(diǎn)的TSP-PC問題的最優(yōu)解能被很快地求出來。在后續(xù)的研究中,可以著手考慮尋找比較好的上界和下界,使動態(tài)規(guī)劃過程中出現(xiàn)的狀態(tài)數(shù)量減少,從而加快求解速度。2 求解算法
2.1 符號和算子


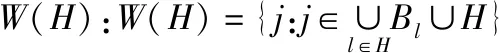
2.2 狀態(tài)轉(zhuǎn)移方程
2.3 算法流程

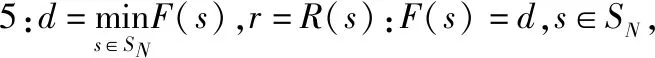

3 數(shù)值實驗

4 總結(jié)
——以物品堆碼為例
——以云南經(jīng)濟(jì)管理學(xué)院為例
——基于貴州省的實證研究
——以中衛(wèi)市沙坡頭區(qū)為例

