頻率分布直方圖經典題型剖析

■胡 磊

頻率分布直方圖屬于一種重要的統計圖表,在統計中具有廣泛的應用。頻率分布直方圖是高考考查的重要知識點,下面對這類題型進行剖析。

一、明確頻率分布直方圖中的相關結論

1.求解頻率分布直方圖問題的關鍵是掌握頻率分布直方圖中的相等關系,其主要關系包括：(1)各小組的頻數之和等于樣本容量;(2)頻率=;(3)各小組的頻率之和等于1;(4)各小組的組距相等,即每個小長方形的寬都相等;(5)各小長方形的高=即小長方形的高與頻率成正比,與頻數也成正比;(6)各小長方形的面積等于各組的頻率,小長方形面積之和等于頻率之和,即為1。

2.利用頻率分布直方圖估計幾種數據：在頻率分布直方圖中,眾數是最高小長方形底邊中點的橫坐標所對應的數據,它表示樣本數據的中心值;在頻率分布直方圖中,中位數是左右兩邊的小長方形的面積相等的底邊的值;平均數等于各個小長方形的面積乘以對應的小長方形的底邊中點的橫坐標之和。

二、頻率分布直方圖經典題型剖析

1.頻率分布直方圖的相關計算。

例1統計某校學生的某次數學同步練習成績(滿分150分),根據成績分成六組：[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],繪制的頻率分布直方圖如圖1所示,若已知不低于140分的人數為110,則該校被統計的學生人數是( )。

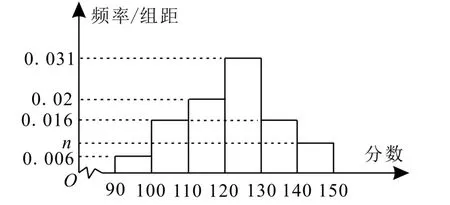
圖1

A.800 B.900

C.1200 D.1000

分析：由頻率分布直方圖可求出n=0.011,從而可得不低于140分的頻率為0.011×10=0.11,由此求出該校被統計的學生人數。

解：由頻率分布直方圖可得10×(0.031+0.02+0.016×2+n+0.006)=1,解得n=0.011。因為不低于140分的頻率為0.011×10=0.11,所以該校被統計的學生人數為應選D。

本題主要考查頻率分布直方圖的有關計算,考查同學們的計算求解能力。

例2港珠澳大橋于2018年10月正式通車,它是中國境內一座連接香港、珠海和澳門的橋隧工程,橋隧全長55km,橋面為雙向六車道高速公路,大橋通行限速100km/h。現對大橋某路段上1000輛汽車的行駛速度進行抽樣調查,畫出了頻率分布直方圖(如圖2)。根據頻率分別直方圖,估計在此路段上汽車行駛速度在區間[85,90)上的車輛數和行駛速度超過90km/h的頻率分別為( )。

圖2

A.300,0.25 B.300,0.35

C.60,0.25 D.60,0.35

分析：由頻率分布直方圖可求出在此路段上汽車行駛速度在區間[85,90)上的頻率,從而求出在此路段上汽車行駛速度在區間[85,90)上的車輛數,再求出行駛速度超過90km/h的頻率。

解：由頻率分布直方圖可得,在此路段上汽車行駛速度在區間[85,90)上的頻率為0.06×5=0.3,所以在此路段上汽車行駛速度在區間[85,90)上的車輛數為0.3×1000=300,行駛速度超過90km/h的頻率為(0.05+0.02)×5=0.35。應選B。

樣本的頻率分布直方圖的畫法步驟：計算數據極差xmax-xmin;決定組距和組數;決定分點;列頻率分布表;畫頻率分布直方圖。

2.利用頻率分布直方圖求平均數、中位數、眾數。

例3某企業對其生產的一批產品進行檢測,得出每件產品中某種物質含量(單位：g)的頻率分布直方圖,如圖3所示,則該物質含量的眾數和平均數分別為( )。

圖3

A.83和84 B.83和85

C.85和84 D.85和85

分析：由頻率分布直方圖中最高小長方形可知眾數落在第三小組,從而求出眾數的值,再由每個小組的頻率以及中間值求出平均數。

解：根據頻率分布直方圖可知眾數落在第三小組,所以眾數為

由含量在[60,70)內的頻率為0.1,含量在[70,80)內的頻率為0.2,含量在[80,90)內的頻率為0.4,可得含量在[90,100)內的頻率為0.3,所以該物質含量的的平均數為65×0.1+75×0.2+85×0.4+95×0.3=84。應選C。

本題主要考查頻率分布直方圖中眾數和平均數的求法,考查運算求解能力。

例4在某次高中學科競賽中,4000名考生的參賽成績統計如圖4所示,60分以下視為不及格,若同一組中數據用該組區間中點作代表,則下列說法中錯誤的是( )。

圖4

A.成績在[70,80]內的考生人數最多

B.不及格的考生人數為1000

C.考生競賽成績的平均分約為70.5

D.考生競賽成績的中位數為75

分析：利用頻率分布直方圖即可判斷四個選項的正確與否。

解：根據頻率分布直方圖可得,成績在[70,80]內的頻率最大,即考生人數最多,A正確。不及格的考生人數為10×(0.01+0.015)×4000=1000,B正確。根據頻率分布直方圖估計考試成績的平均分為45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5,C正確。由前四組的頻率大于0.5,前三組的頻率等于0.45,可知中位數在第四組,可得考生競賽成績的中位數為錯誤。應選D。

在頻率分布直方圖中,眾數是最高小長方形底邊的中點所對應的數據,它表示樣本數據的中心值;中位數左邊和右邊的直方圖面積相等,由此可以估計中位數的值,但有偏差;平均數等于每個小長方形的面積乘以小長方形底邊中點的橫坐標之和,平均數是頻率分布直方圖的“重心”,它是頻率分布直方圖的“平衡點”。