斜支柱小水線面雙體船水動力性能的數值研究

毛立夫，李英輝，易 宏

(上海交通大學 海洋智能裝備與系統教育部重點實驗室; 海洋工程國家重點實驗室;高新船舶與深海開發裝備協同創新中心, 上海 200240)

小水線面雙體(SWATH)船是一種通過流線型支柱連接排水部分及水上部分的船型[1]，其排水體積主要集中于除支柱外的水下部分(魚雷體)，因其深埋于水中，故受到的波浪干擾力、在大風浪中的失速、運動響應幅值、運動加速度幅值均較小.此外，與排水量相當的常規單體船及雙體船相比，該船型的水線面較小，縱搖及橫搖固有運動周期較大，在斜浪中不易發生斜搖，具備優良的耐波性能.SWATH船具有適于遠洋航行、風浪中出航率高、波浪失速少、暈船率低、工作效率高等優點[2]，在海上交通、海洋調查、水聲監測等領域受到了廣泛的應用.目前，在新興的水面無人艇領域的應用也備受關注[3].除了采用常規直立支柱的SWATH船外，具有良好隱身特點的斜支柱小水線面雙體(I-SWATH)船也逐漸得到了開發與應用[4].

較小的水線面積能使SWATH船獲得較大的垂蕩、縱搖及橫搖固有運動周期，從而避開與中等以下海浪的主要波頻成分發生諧振，降低波浪中的運動響應.但其垂蕩及縱搖回復力(矩)相對較小，在對應的諧振頻率處其響應峰值較高.當有義波高較低時, SWATH船具有較小的暈船率(MSI)；但當有義波高大于3.0m (高于四級海況)后，MSI將會快速增大，導致船員和旅客的舒適感降低.這是由于隨著有義波高的增加及波浪周期的延長，SWATH船的遭遇頻率逐漸靠近最大響應頻率(諧振頻率)，致使運動響應越來越劇烈[5].為了改善SWATH船耐波性能的不足，研究人員研發出一種具有傾斜支柱的SWATH船.

有關SWATH船的水動力性能，國內外的學者做了大量研究.如毛筱菲[6]、劉志華等[7]均基于二維切片理論，采用半經驗方法考慮黏性及穩定鰭的影響，對SWATH船的耐波性進行了大量的數值研究.林鵬等[8]基于重疊網格技術研究縱向航態對SWATH船的阻力影響.考慮模型試驗的尺度效應，Dubrovsky 等[9]分析了SWATH船的形狀阻力并總結了影響剩余阻力的因素.Lei 等[10]基于雷諾平均Navier-Stokes (RANS)方程和流體體積(VOF)模型求解黏性興波流場，并開展了SWATH船在迎浪規則波中縱向運動及波浪載荷的非線性研究.然而，除了Brizzolara等[1,3]對一艘內傾式支柱SWATH船水下潛體的阻力進行優化外，上述學者的研究工作多集中于常規直支柱的SWATH船上.

傾斜支柱的最初設想源于Techet[11]關于將振動翼作為新型高效船用推進器的研究設想.鑒于振動翼自身類似魚鰭的二維擺動能夠產生推力，當具有傾斜支柱的SWATH船在波浪中進行垂蕩及縱搖運動時，斜支柱的運動形式類似于振動翼的二維擺動，因此可能能夠利用由波浪產生的推力[12-13].為此在前期工作[4,14-16]中，運用 STF(Salvesen，Tuck，Faltinsen)切片理論考慮片體之間的干擾，對I-SWATH船的耐波性進行頻域分析，并基于RANS方程對其在低速段(弗勞德數Fr<0.35)的耐波性做了初步研究，發現其波浪增阻較小，運動響應呈現出一定的非線性，且運動周期大于波浪遭遇周期.

但由于STF切片理論忽略了黏性阻尼，運動響應的計算結果往往偏高.雖然能夠獲得垂蕩、縱搖及波浪增阻的大致變化規律，但在每個遭遇頻率下的計算精確度較差(尤其在高速段Fr>0.4)，并不能反映出局部細節的特性.此外，雖然I-SWATH船的片體和支柱可以看作是細長體，但由于傾斜支柱與自由面是斜交的，形成的不對稱流場引起的泄渦在很大程度上影響了阻尼和阻力.Latorre等[17]通過模型試驗及數值計算，發現黏性對運動響應預報有較大的影響.因此，為了進一步研究該船型在波浪中的運動響應，本文利用考慮黏性阻尼的三維面元法進行頻域分析，改善計算結果的精確度；然后，基于求解 RANS方程的黏流理論，對該船型在規則波中的水動力性能進行數值計算；數值模擬中運用重疊網格方法[8]，更好地模擬了高航速下船體的大幅度運動，拓展了前期的研究工作，獲得了更加合理而精準的結論.

1 模型介紹

基于前期關于I-SWATH船的研究[4,14-16]，所研究的船體輪廓圖如圖1所示，其主要參數取值如表1所示.其中，數值計算模型與實船的縮尺比為 1∶10.

圖1 I-SWATH船的輪廓圖Fig.1 The porifiles of I-SWATH ship

表1 I-SWATH船的主尺度參數Tab.1 Principal dimensions of I-SWATH ship

這種非常規SWATH船的設計初衷是在惡劣海況下，探究利用傾斜支柱作為水面無人艇的適航性及生存能力.根據仿生流體動力學[18]及魚的形狀，將傾斜支柱設置在船尾附近，以期傾斜支柱可通過水下魚雷體引起的流動產生推進力.本文重點探究了I-SWATH船在迎浪規則波中的水動力性能，為了簡化問題，在所有數值模擬中均不考慮上層結構.

2 基于三維面元法的耐波性頻域分析

在單體船中，三維勢流理論已經被廣泛地應用于計算船體的耐波性，且其計算精度較好.但對于雙體船而言，除了直接應用三維勢流理論，還需要考慮黏性阻尼對于船體垂蕩及縱搖的影響.大量的理論及試驗研究表明：在不考慮黏性影響的情況下，直接使用三維勢流理論計算雙體船的運動響應(垂蕩及縱搖)將會導致計算結果明顯偏大.

圖2 船體的坐標系及其運動Fig.2 Depiction of ship coordinate systems and its motions

2.1 坐標系

為了描述船體的6自由度運動，建立兩套右手直角坐標系，如圖2所示：大地固定坐標系O-XYZ和固定在船上的隨體坐標系o-xyz.前者固定在流場中，不隨流體或船體運動；OXY平面與靜水面重合，OZ軸豎直向上.后者隨船體一起運動，其坐標原點在船體的重心處；ox軸位于縱中平面內并指向船首，oy軸指向左舷；當船舶處于平衡位置時，oxy平面與靜水面平行，oz軸豎直向上.

2.2 基本方程及其邊界條件

設船以恒定速度U航行，暫不考慮舵、鰭、槳的影響；基于三維勢流理論，假定流體為無黏、均勻、不可壓縮的無旋流體；船體視為剛體，在平衡位置做6自由度的搖蕩運動；入射波為微幅波，則船體各模態的搖蕩運動可視為遭遇頻率為ωe的簡諧振動.用標量函數速度勢Φ(x,y,z,t)描述速度分布.該速度勢包括船體恒速航行時產生的定常速度勢Φs(x,y,z)、入射波速度勢Φ0(x,y,z,t)、入射波遭遇船體時產生的繞射勢Φ7(x,y,z,t)、船體搖蕩運動時產生的輻射勢ΦD(x,y,z,t).根據線性勢流理論的疊加原理，總速度勢可以表示為

Φ(x,y,z,t)=Φs(x,y,z)+Φ0(x,y,z,t)+

Φ7(x,y,z,t)+ΦD(x,y,z,t)

(1)

將非定常速度勢部分的時間因子分離出來，可以寫成以下形式

Φ0(x,y,z,t)+Φ7(x,y,z,t)+ΦD(x,y,z,t)=

(2)

式中：i=1,2,…,6;φ0為入射波的空間速度勢；φj為6自由度運動各模態所對應的規范化速度勢，j= 1, 2,…，7；Xj為6自由度運動各模態所對應的運動幅值，j= 1, 2,…，7；當j=1,2，…，6時，分別為船體的縱蕩、橫蕩、垂蕩、橫搖、縱搖和艏搖運動，當j=7時，為繞射勢的空間速度勢.

規則入射波的速度勢可以為

(3)

式中：a為波幅；λ為入射波長；β為入射波浪向角；k=2π/λ為波數；ω為波浪頻率；H為水深；g為重力加速度.k與ω滿足色散關系ω2=gktanhkH.

繞射勢和輻射勢應滿足以下邊界條件：

流域內

Δφj=0,j=1,2,…,7

自由液面上

j=1,2,…,7

濕表面上

當z=-H時

輻射條件

(4)

2.3 船體運動方程

通過上述速度勢可求解波浪力，代入船體在波浪中的運動方程即可求解船體的運動

(5)

i=1,2,…,6;j=1,2,…,6

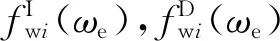
2.4 黏性阻尼

對于常規單體船豎直面內的運動，由于興波阻尼占主要部分，黏性阻尼常被忽略不計.然而，SWATH船的片體被埋在水下，產生的水面興波較小，興波阻尼所占比例也相對較小.此外，由于其水下片體的橫向尺度要大于支柱，且傾斜支柱與自由面是斜交的，形成的不對稱流場引起的泄渦在很大程度上會同時影響阻尼和阻力，所以黏性阻尼不能忽略.否則，計算得到的運動幅值在響應頻率附近將呈現出典型的欠阻尼線性導致計算結果的正確率有所下降[19].

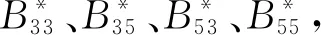
計算上述附加水動力系數以及干擾力時，所需的交叉流阻力項需要預先知道船體的運動幅值，所以可以先不考慮交叉流阻尼，利用式(6)求出運動幅值；然后，利用該幅值計算交叉流阻力項獲得附加水動力系數和附加干擾力并代入式(6)，進而獲得考慮黏性阻尼的運動幅值；按此方法反復迭代直到獲得一個合理的收斂結果，通常迭代3～5次即可[20].

高校的教育目的是為了社會需要培養優秀人才，為了企業需求培養定向型專業人才，隨著社會形式的不斷發展，社會對人才水平的需要也在不斷提高。經濟管理專業與社會發展、地方經濟有著不可忽視的關系。經濟管理高校以培養經濟管理操作能力與管理理論兼具的經濟管理專業型人才為目標，在知識理論與實際相結合的前提下，大大提高經濟管理人才的培養效果，同時也有利于形成學校和企業雙贏的局面。經濟管理教學要與當下社會經濟環境相融合，有針對的為社會經濟需要培養相應經濟管理人才。傳統的經濟管理教學已不能滿足現今社會發展速度，校企合作模式是通過企業對人才實際需要的前提下，聯合高校共同建立培養企業所需人才的機制。

2.5 計算結果

2.5.1算法驗證 利用上述方法考慮黏性阻尼的影響，通過自編程序計算得到的迎浪時代爾夫特雙體船(Delft-Cata)與試驗數據(TS1)[21]以及切片法(STF)的垂蕩及縱搖運動響應幅值算子(RAO)計算結果的對比情況如圖3所示.由圖3可知，考慮黏性阻尼后，STF與TS1的計算結果吻合程度更高，在一定程度上能夠提供更多的局部細節特征，可用于進一步探究I-SWATH船的耐波性能.

圖3 TS1和STF的計算結果與Delft-Cata的試驗結果對比圖Fig.3 The experimental results of TS1 and STF calculation results compared to Delft-Cata test results

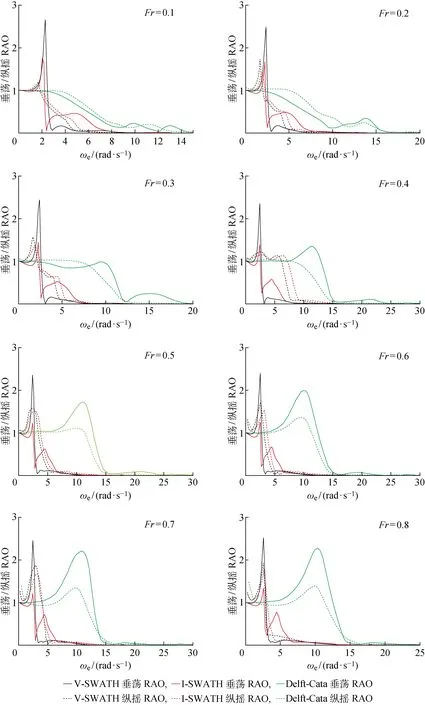
圖4 I-SWATH與V-SWATH和Delft-Cata的垂蕩和縱搖RAO對比Fig.4 Comparison of the heave and pitch RAO calculated for I-SWATH, V-SWATH and Delft-Cata

3 靜水與規則波中的水動力性能

3.1 數值計算原理

由于非常規SWATH船的傾斜支柱與自由面斜交，所形成不對稱流場引起的泄渦在很大程度上影響了阻尼和阻力.為了充分考慮黏性，基于RANS方程采用同質多相流Euler方法捕捉自由液面.假設在每個空間有單一的時間平均速度場ui(i=1,2,3, 分別代表x、y、z3個方向),則不穩定的黏性流體控制方程為

(6)

(7)

式中：p為壓力；ρm為混合密度；ρα和rα分別為介質α的密度和體積系數，其中α=1代表介質為水，α=2代表介質為空氣；μm為混合黏性系數.則有

增量方程采用的湍流模型為SSTk-ω方程，壁面函數為All Y+型，并加入6自由度剛體運動計算模塊以及波浪生成模塊.采用規則波浪，其波浪方程定義如下：

z=acos(kx-ωe+δ)

(10)

式中：δ為初始相位.

波數和波浪頻率滿足色散關系.根據線性波浪理論，規則波的速度勢為

(11)

進而得到水質點在x、z方向的速度分量分別為

(12)

(13)

波浪生成模塊與RANS方程的結合已經在前期工作[4]中得到了驗證，可用于本研究.

3.2 網格劃分及邊界條件

對于所有計算，按照主尺度為1∶10的縮尺比建立長度為2.0 m的船模，相應的計算域及邊界條件如圖5所示.由于船體的對稱性，數值模擬利用邊界對稱條件只需構建半邊船模.計算域的大小在x方向：-5l

圖5 計算域及邊界條件Fig.5 Computational domain and boundary conditions

作為剛體，為更準確地模擬船體在波浪中的運動，采用重疊網格技術[8].整個計算域分為靜止部分(定域)和運動部分(動域)，前者是背景網格，后者則為包覆著船體的動網格，嵌套在背景網格中.相比動網格技術，重疊網格在處理大幅度運動時更具有優勢.由于不需要重新生成網格，所以不會出現負體積等動網格的缺點，同時相對于沉浸邊界法而言，具有更好的計算精度.網格數量約為3×106個，網格的劃分細節如圖6所示.在船體、自由面及動域附近都進行局部加密，船體表面設置邊界層以模擬湍流邊界，其他遠域網格尺寸相對較大以節省計算時間[16].

圖6 重疊網格劃分Fig.6 Overset meshes

計算域的入口速度設置為基于船長的Fr，出口為靜水壓力邊界條件；由于船體對稱，中心平面可視為對稱面；船體表面為不可滑移壁面，底面及遠域壁面均設置為自由滑移壁面，頂部為具有恒定大氣壓的開闊邊界；計算時間步長取Te/200(Te為波浪遭遇周期).

3.3 靜水阻力

基于RANS方程的數值模擬獲得的靜水總阻力(Rt)結果與文獻試驗數據[16]進行對比，結果如圖7所示，其中R=Rt/(Vρα)，此處α=1.數值計算結果中的摩擦阻力(Rf)是通過對船體表面的切向力求和獲得的，剩余阻力 (Rr)是通過對船體表面法向力在船舶前進方向求和獲得的.船模試驗結果中的摩擦阻力是利用1957年國際船模試驗水池會議(ITTC)上提出的公式計算獲得的[4]，剩余阻力是由總阻力減去摩擦阻力獲得的.

由圖7可知，2種方法得到的摩擦阻力吻合得較好，而剩余阻力之間存在著較大的誤差.在所計算的Fr范圍內，摩擦阻力隨著Fr的增加而增加.當0.1

圖7 I-SWATH船的靜水阻力曲線Fig.7 Resistance curve of I-SWATH ship in calm water

不同航速下，對應船體周圍的興波輪廓圖如圖8所示.由圖8可知，當Fr=0.48，0.60時，船體后方的興波更為嚴重；而當Fr=0.72時，興波相對較小.對于水面船舶，興波阻力通常是剩余阻力的主要組成部分.因此，較大的興波導致阻力增加，而較小的興波有利于減小阻力.當Fr=0.36時，附近出現阻力谷值，可能是由于此時船舶片體間的有利干擾使得興波相對較弱，進而導致興波阻力較小.當Fr=0.48時，由拖模試驗與數值模擬得到的船體表面處的自由液面情況如圖9所示.由圖9可知，二者吻合得較好，可以驗證所采用的數值模擬方法捕捉到的自由液面精度較高，能夠進一步研究水動力性能.

圖8 靜水中不同航速下的興波圖Fig.8 Free surface elevation contours of the fixed model in calm water

圖9 當Fr=0.48時斜支柱表面的自由液面Fig.9 Free surface elevation along the struts at Fr=0.48

3.4 靜水和規則波中的計算

為了進一步探究斜支柱的作用，增加具有豎直面內自由度的數值模擬.為簡化問題，模型暫不考慮舵、鰭和槳的影響.不同于模型試驗中水池及測量設備等物理條件的限制，數值模擬能夠提供更多的工況選擇，獲得更高速度下的阻力及運動響應計算結果.規則波中數值模擬的工況如表2所示.其中，h為波高；ak=πh/λ為波陡.由數值計算得到的靜水及規則波中的阻力及運動結果如表3所示.其中，波浪增阻(Radd)為波浪中的總阻力減去靜水總阻力.阻力(Rt、Rf、Rr)、縱傾角(θ)及沉深(η)均取為自計算穩定收斂后的平均值.

表2 數值模擬的工況Tab.2 Cases of numerical simulations

表3 靜水和規則波中阻力及運動的數值計算結果Tab.3 The calculated resistance and motions in calm water and in head waves for free model

由表3可知，當Fr=0.30時，靜水縱傾角達到峰值，此處靜水阻力也出現了局部峰值(見圖7).除了當Fr=0.25，0.30，0.35時，波浪增阻出現了負值以外，其他航速下波浪中的阻力均大于靜水阻力.波浪中阻力的增加與波高、平均縱傾角及平均沉深的變化是密切相關的.一方面，這些量的改變直接導致了船體濕表面積的變化，進而影響摩擦阻力；另一方面，這些量是船體在波浪運動狀態中的一種客觀體現，能夠影響剩余阻力.當Fr=0.25，0.30，0.35，且波浪條件為λ/l=0.6，1.0時，波浪增阻出現了負值，這可能是由于平均縱傾角和沉深的減小所導致的.但是當波浪條件為λ/l=1.5時，平均縱傾角及沉深都是增大的，波浪增阻依舊出現了負值.這種現象的出現應該與傾斜支柱有關，船體在波浪中做垂蕩及縱搖運動時，傾斜支柱的運動形式類似于振動翼的二維擺動而能夠利用由波浪產生的推力[13, 18].

利用快速Fourier變換(FFT)及Fourier級數展開(FS)相結合的頻譜細化方法[22]分析計算所得的運動響應時歷曲線，獲得不同航速下的垂蕩及縱搖RAO，如圖10所示.由圖10可知，運動響應呈現較強的非線性.垂蕩RAO隨著遭遇頻率的變化呈現出明顯的雙峰值，不同Fr下的兩個峰值分別出現在大致相同的兩個遭遇頻率處(約為3.2 rad/s和4.9 rad/s)，且隨著Fr的增加，第1個峰值逐漸減小，第2個峰值逐漸增大.隨著Fr的增加，縱搖RAOs的峰值大致呈現出先減小后增大的變化趨勢. 當Fr=0.10，0.20，0.30時，縱搖RAOs峰值逐漸減小且大致出現在相同的遭遇頻率處(約為3.5 rad/s)；當Fr=0.40，0.50時，縱搖RAO峰值逐漸增大，但出現在更大的遭遇頻率處(約為4.2 rad/s)，因此當Fr=0.30附近時，縱搖RAO的峰值存在極小值.而當Fr=0.25，0.30，0.35時，波浪增阻確實出現了負值.這種情況可能與傾斜支柱有關.當船體在波浪中進行垂蕩及縱搖運動時，后置的傾斜支柱運動形式類似于振動翼的擺動而能利用由波浪產生的推力，使波浪增阻出現負值.此外在相同波長條件下，較高航速時的垂蕩及縱搖RAO反而相對較小，這也符合SWATH船低速時的穩定性不及高速時穩定性好的特點.但從整體而言，這種特殊的SWATH船比常規的雙體船具有更良好的耐波性能.

圖10 不同航速時的垂蕩與縱搖RAOsFig.10 The heave and pitch RAOs at different speeds

4 結論

本文介紹了一艘具有傾斜支柱的非常規SWATH船，通過數值模擬方法對其在靜水及規則波浪中的水動力性能進行了研究.研究結果表明：傾斜支柱在改善耐波性能方面具有一定的優勢，并對此進行了相關的分析討論.

(1) 利用考慮黏性阻尼的三維面元法對這種非常規SWATH船在波浪中的運動響應進行頻域分析，改善了計算結果的精確度；討論垂蕩及縱搖RAO，為后續的數值模擬提供了波頻選取的合理參考.

(2) 為了進一步探究該船型的水動力性能，考慮黏性和自由液面，將RANS方程與波浪發生模塊及6自由度剛體運動計算模塊整合在一起，預測該船在靜水及頂浪規則波中的運動和阻力性能.與模型試驗的結果進行對比，驗證該數值計算法的準確性.

(3) 由于其船型的特殊性，該船在波浪的水動力性能方面具有很強的非線性.垂蕩及縱搖運動RAO隨遭遇頻率呈現出雙峰值.導致該種現象的原因一方面是由于片體間的干擾，另一方面是由于傾斜支柱的影響，進而導致了該船具有較強的運動非線性，所以對此船型的研究工作必須仔細處理這些非線性性能.

(4) 數值模擬結果中出現負值的波浪增阻，表明傾斜支柱可以利用波浪減少在波浪中航行所需的能量.然而，斜支柱的這種功效并不明顯，未來還應通過更多的模型實驗進一步研究該船型的這一特性.