用好問題引領兒童數學學習

李瑾

[摘要]好的問題能引領兒童數學學習，促進兒童深度思考。通過對專家和新教師課堂教學中的提問進行對比和分析，發現好問題一定指向“數學學科本質和核心價值”，蘊含“學習方式與理解路徑”，且能激發兒童的“探究熱情和欲望”。

[關鍵詞]好問題;兒童;數學學習

[中圖分類號]G623.5 [文獻標識碼]A [文章編號] 1007—9068（2019）32—0003—03

問題是兒童學習的目標、動力和途徑，問題引領兒童學習數學的過程，讓學生從知識的接受與獲得，轉化為親身體驗“知識的生成和建構”，并促進兒童進行深度思考，從而獲得數學成長。好的問題將能引領學生學習的發生和深入，那什么是能引領兒童數學學習的好問題呢？我們工作室的教師一方面關注自己課堂教學中的問題設計，同時也嘗試對比專家和新教師在同一課題下的課堂提問，探尋好問題的共性。

【案例1】“認識平均數”（蘇教版教材四年級上冊）

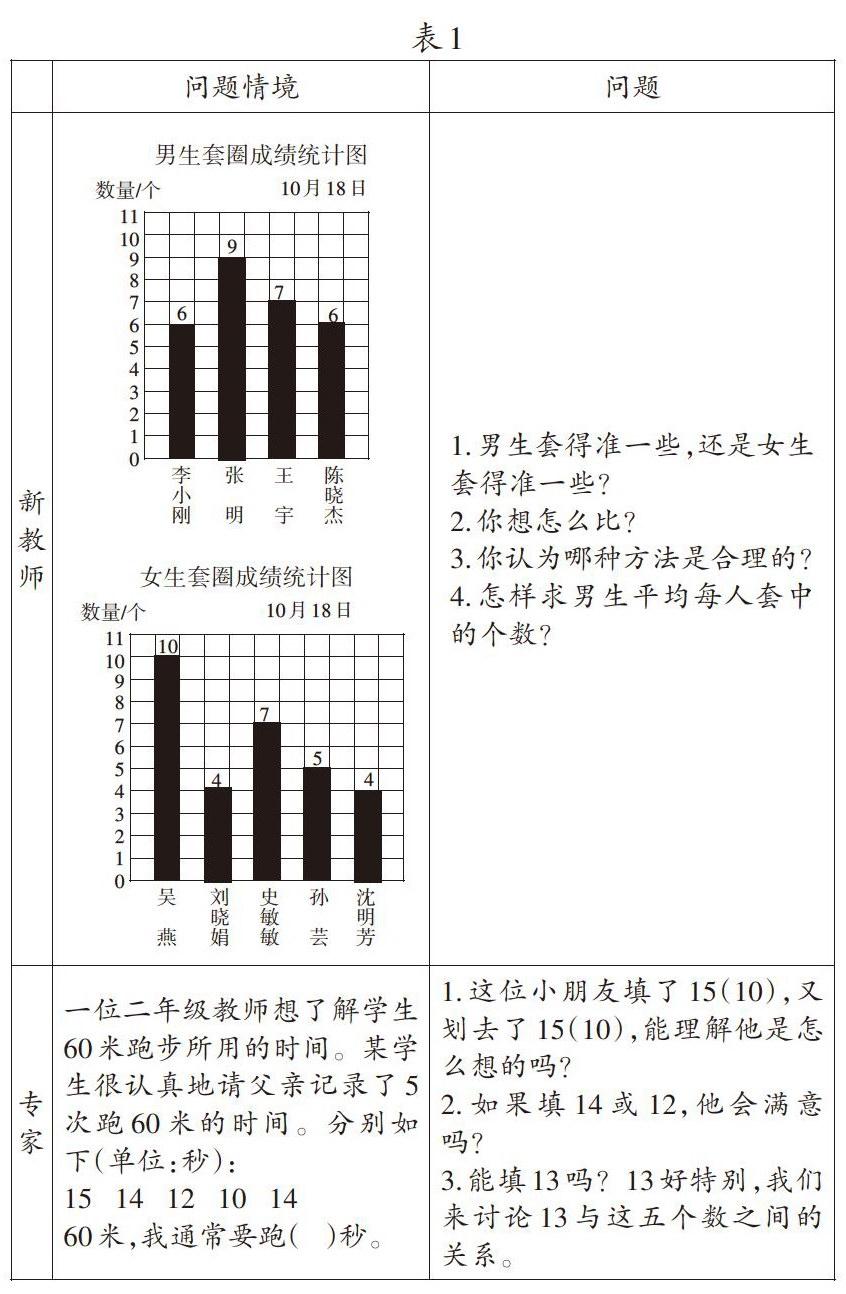
一、案例呈現（如表1）

二、案例分析與思考：好問題應指向數學學科本質和核心價值

1.對問題的分析

平均數可以把一組數據作為一個整體進行描述，是小學階段“統計與概率”領域中唯一一種統計量。要完整理解平均數的意義，需要理解兩個要點，即平均數描述了一組數據的整體水平，以及平均數具有虛擬性。

對平均數的概念及其內涵了解之后，進一步分析新教師和專家所給出的問題。

新教師所提出的4個問題中，前3個問題指向的是什么情境下使用平均數，第4個問題指向的是平均數的計算方法。概括起來就是“情境”與“公式”，即今后遇到類似情境就運用這個公式，是通過重復的應用幫助學生形成解題的能力。

專家在“問題情境”中提出的一個大問題“60米，我通常要跑（ ）秒。”，直接指向尋找一個能代表一組數據整體水平的數，即平均數的代表意義。其后給出的三個問題都是引領學生對平均數的代表意義做出思考與討論。尤其是13與五個數之間的關系，既包含了平均數的虛擬性特征，又蘊含了平均數的計算方法。概括起來就是通過合適的問題情境與問題促進學生感受并自主構建平均數的概念及對要點的理解。

2.思考：好問題應指向數學學科本質和核心

由上述分析可以看出，新教師與專家在設計問題的過程中都關注到了兒童的已有經驗和教學目標，但新教師所設計的問題容易使學生對概念的理解出現缺失：學生知道平均數有什么作用，怎么得到，但是卻不知道平均數到底是什么。而專家給出數據后所引出的問題“60米，我通常要跑（ ）秒。”情境相對復雜，但是直接指向了數據分析，能夠引領學生有意識地從數據的角度思考有關問題，盡管這個時候還沒有學平均數的意義和求法，但是學生尋找可以代表一組數據整體水平的數據的過程，實際上已經指向平均數的意義，這種自發的、非正式的認識，無疑有助于學生更好地構建平均數的概念，以及體會這個統計量的作用。

正如張奠宙教授認為，一個好問題要能體現數學本質，具有數學價值，能夠啟發學生進行深度的數學思考。即教師需要分析和發掘教學內容與目標所包含的核心問題，并圍繞其提出供學生研究和思考的問題，而新教師恰恰在對數學概念本質的理解上與專家存在差異。因此，要尋求這樣的好問題，教師不僅要關注教材，更重要的是理解與掌握教材內容中的數學知識本身，這樣才能發掘更多指向數學學科本質核心與價值的優質問題。

【案例2】“認識面積”（蘇教版教材三年級下冊）

一、案例呈現

二、案例分析與思考：好問題應蘊含學習方式與理解路徑

1.對問題的分析

面積概念的意義建構需要學生調用已有的生活經驗，并在操作活動中不斷感受，從而使得學生對面積意義的理解更加全面。新教師和專家都調用了學生已有的生活經驗，但是新教師認為學生的經驗是“面是有大小的”，因此給出的問題均是從面的大小出發，讓學生通過比較兩個面的大小，初步理解面積的含義，最后運用面積概念進行比較。“喚起經驗——得出概念——進行運用”是從教的角度給出的理解路徑。

專家所提出的問題也是基于學生的經驗基礎，但不忽略學生在生活中對面積的有所了解，從“在哪里聽說過？”和“你有什么問題？”開始了解學生的現實起點，然后讓學生通過描線和涂色的操作對比（實質上是周長和面積的比較），初步感知什么是面積，最后再回到生活中感受什么是面積。這是一條“現實起點出發——與相關概念對比學習——回到生活深入理解——完成概念建構”的理解路徑。

2.思考：好問題應蘊含學習方式與理解路徑

運用數學的思維方式進行思考，學會數學地思考，是問題解決中明確提出的培養學生創新意識和實踐能力的目標，也是決定數學課程改革方向的基本載體。從學生熟悉的情境開始，運用問題解決的路徑，如上述面積概念的建構中，專家提出的問題中就蘊含“數學現實——對比學習——逐步數學化——概念建構”的理解路徑。尤其是在相關概念的學習過程中，通過對周長和面積形象化的感知，學生不僅建構了面積概念，也再次完善了周長概念。

在上述理解路徑的基礎上，專家提出的問題還有利于學生之間的對話、合作與反思。像這樣蘊含學習方式和理解路徑的問題，需要把握住兒童數學現實與學科課程目標之間的距離，而實現這一距離的跨越就是設計合理豐富的學習方式與符合兒童心理的理解路徑，以達到用數學任務和設計的數學問題幫助學生“學會思維”的目的。

【案例3】“表面涂色的正方體”（蘇教版教材六年級上冊）

一、案例呈現

二、案例分析與思考：好問題能激發兒童的探究熱情和欲望

1.對問題的分析

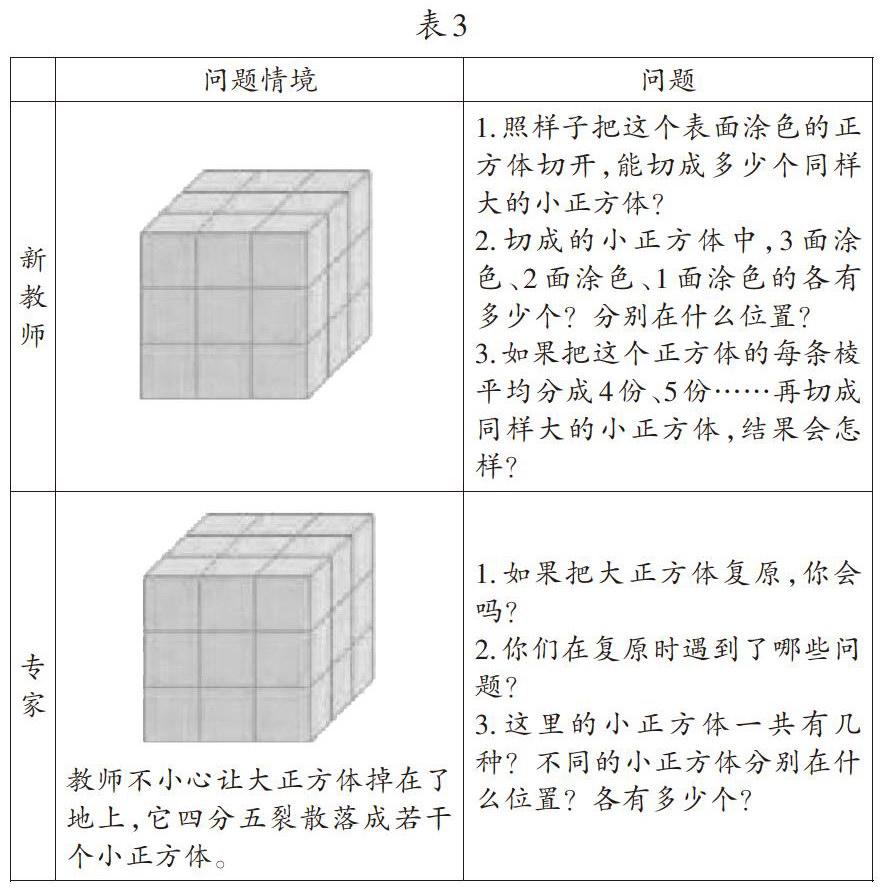
在“表面涂色的正方體”一課中，學生需要想象出把大正方體的每條棱平均分成3份并切開，小正方體表面涂色的不同情況及每種小正方體的個數和位置，從而為后面的規律探索奠定基礎。

兩個課例情境相仿，都是先呈現一個表面涂色的大正方體（每條棱都平均分成了3份），然后提出問題。

新教師給出的問題中，“3面涂色、2面涂色、1面涂色的各有多少個？分別在什么位置？”及后續的第3個問題，看似給了學生主動探究的機會，但實際上是教師指令性的觀察與操作，學生始終處于接受指令、被動思考與探索的狀態之中，無法激起學生探究的欲望。

專家通過掉落的大正方體，提出了“如果把大正方體復原，你會嗎？”這種具有挑戰性的游戲任務，能夠滿足學生對游戲天然的喜愛，可以點燃他們主動觀察、操作的熱情火花，而在復原失敗后，因為不服輸精神，探究與思考成為他們內在的需求，教師提出的反思性問題（復原的過程中遇到了什么困難）與提示性問題（這里的小正方體一共有幾種？不同的小正方體分別在什么位置？各有多少個？）為他們指明了探究的方向，激發了他們探究的欲望。

2.思考：好問題能激發兒童的探究熱情和欲望

問題，尤其是具有數學任務的問題，是啟發學生開展數學思考的核心動力，但是若無法吸引學生參與討論則會失去其價值與意義。一個好的問題，對每個個體而言都是獨特的，讓每個學生都可以參與到其中進行思考。如上述專家給出的“復原”任務與問題，看似并沒有提出觀察每個小正方體，實際上，“復原”任務中包含著對正方體的觀察，及其所處位置的思考。因其游戲的形式，使得每個學生都可以參與其中，容易激起學生思考的欲望，并引發學生之間的討論，同時又有向縱深發展的余地。

張奠宙教授在好問題的標準中提出的第一條就是要能引人入勝，激發學習者思考的欲望，因此能夠激發兒童的探究熱情和欲望的好問題就是數學思考的良好開端。我們在把握學科本質的基礎上需要多研究兒童，研究他們的天性和心理規律，以尋找與兒童現實及學科本質相匹配的問題，激發兒童的探究熱情和欲望。正如華應龍老師在《好課如初戀般美好》一文中談到，“幾何是和想象力玩耍的玩具”，課上學生還沒有玩起來，還沒有玩夠，教師就匆匆忙忙揭示規律，倉促“登堂入室”，就像一個小孩尚未長大，你就要他承擔大人的角色，那是操之過急了。數學中可以玩的元素很多，應該從生動、有意思，及玩好數學的角度設計好問題，以此激發兒童進行探究。

從以上所呈現的案例和分析可以看出，新教師與專家所設計的問題具有差異性，專家設計的問題情境與問題往往指向學科本質與核心價值，蘊含著豐富的學習方式與理解路徑，能激發兒童的探究熱情與欲望。文中每個案例的分析雖然僅涉及其中某一個角度，而好的問題往往同時兼具三個方面的特征，三者之間的關系如下圖所示：

通過對比不同教師所設計的問題，能引發我們對“好問題”的思考，并進一步探尋如何設計“好問題”。教師要加強對數學學科本質的掌握與理解，更新兒童觀，并以學習路徑作為溝通學科與兒童之間聯系的橋梁，深入理解三者之間的關系，從而設計出“好問題”來引領兒童的數學學習。

（責編 金鈴）