保持平行關系中的重合特例
謝佳慧
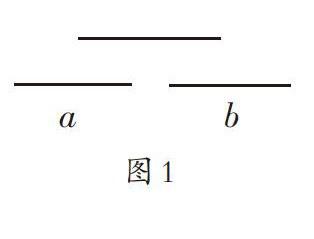
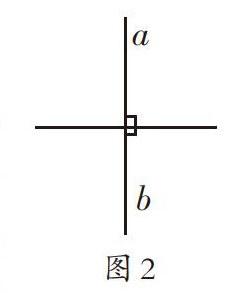
[摘要]保持平行關系是小學幾何圖形中常見的幾何位置關系,但是對于保持平行關系概念的主體到底是線段還是直線并沒有嚴格的界定,有時線段保持平行關系與直線保持平行關系的不同表述會使學生在理解上產生歧義。線段保持平行關系是指線段所在的直線保持平行關系,這樣保持平行關系就存在一個重合問題,即兩線重合算不算保持平行關系。
[關鍵詞]平行關系;重合;質疑;反思
[中圖分類號]G623.5 [文獻標識碼]A [文章編號] 1007—9068(2019)32—0030—01
一、精彩的質疑和求教
一天,有兩個女生來找我評理,一個女生說:“老師,我覺得兩根火柴棒這樣子擺放(如圖1的a和b)后,它們似乎不再保持平行關系了。”“可隔壁班的老師堅持說是保持平行關系的。”另一個女生不服氣地說。
兩個女生爭論的問題源于人教版教材第七冊第65頁的第2題“擺一擺:(1)讓兩根火柴棒同時與第三根火柴棒保持平行關系,觀察一下,這兩根火柴棒能不能保持平行關系?(2)讓兩根火柴棒同時與第三根火柴棒垂直,看一看這兩根火柴棒的位置關系如何”。這兩個問題,前一個直接淺白,后一個復雜隱晦,難度逐步加大,思維含量高。我思考片刻,回復她們:“圖1的擺法沒有錯,符合條件,別具一格。但是一旦出現這種情況,兩根火柴棒就無法構成平行關系,這是一種特殊情況,嚴格來說,應該叫作兩根火柴棒在同一直線上。”無獨有偶,后來我在正式講授第(2)題時,也有學生擺出異常的情況(如圖2)。
圖1和圖2的情況不能認定為互相保持平行關系,但火柴棒作為有長度的木棍,可視為線段,出現這兩種特殊情況情有可原。可教材沒有正式提出“兩條線段在同一直線上”這一空間定義,四年級的學生能不能無師自通、不言自明?要不要老師進行專題講解?教了能否聽懂?如果不講解,在遇到上述特殊情況時如何處置?……一連串的問號出現在我的腦海里,久久無法解開。
二、爭論后的反思
教材安排這兩道題,其目的在于讓學生通過操作、反思、辨析,總結歸納出兩條推論:一是兩直線同時與同一平面內另一條直線保持平行關系,那么這兩直線也構成平行的位置關系;二是兩條直線同時與同一平面內另一條直線垂直,那么這兩條直線也構成平行的位置關系。因為這兩條推論到了初中,就成為兩條定理,可見這兩條推論成為小學數學與中學數學的銜接橋梁。顯而易見,課本編排這兩道題,是科學合理的,是有著深遠意義的。
教師首先要弄清直線與線段的異同:線段有兩個端點,是截取直線的一部分而得到,其長度是具體可測的;而直線是沒有端點限制的,其長度不受限,因此不可測。可以說,直線是由無數條線段無間隙連接而成。
三、反思后的實踐探索
師:這兩根火柴棒在幾何學上屬于線段還是直線?
生1:線段。
師:若將圖1中水平放置的兩根火柴棒都視為直線,那么會有什么情況發生?這兩條直線最終會有什么神奇變化?
生2:與自身重疊了。
師:與自身重疊后,變成了幾條直線?
生3:合為一體,變成一條直線。
師:一條直線存在保持平行關系這一說嗎?或者說直線能與自己保持平行關系嗎?
生4:不能。
師:那么兩條直線同時平行于同一平面內的另一條直線,這兩條直線如果沒有重疊,會構成什么位置關系?
生5:互相保持平行關系。
同理,兩條直線同時垂直于同一平面內另一條直線,這兩條直線如果不重合,會構成什么樣的位置關系?有了前一題積累的經驗和打下的基礎,學生會立馬認定:它們的位置關系是互相保持平行。在此基礎上讓學生練習鞏固。如:(1)兩根火柴棒同時與第三根火柴棒保持平行關系,觀察一下,這兩根火柴棒構成( )的位置關系;(2)兩條線段同時垂直于同一平面內的另一條線段,判斷一下,這兩條線段構成( )的位置關系;(3)兩條直線同時與同一平面內的另一條直線保持平行關系,那么,這兩條直線構成的( )的位置關系;(4)兩條直線同時垂直于同一平面內的另一條直線,那么,這兩條直線( )。A.互相保持平行關系;B.互相保持垂直關系;C.互相保持平行關系或在同一直線上;D.無法判斷。
筆者將反思所得應用于課堂教學,驚奇地發現,效果特別好,學生對于“兩根火柴棒(線段)置于同一直線上”這一幾何特性,均能夠輕松掌握。特別是做過一組題目后,學生不但嚴格區分開了線段和直線,搞清了它們之間的異同,而且解決了上述兩題,更為重要的是,為初中平行關系性質定理的學習打下了基礎。
(責編 黃春香)

