運算律復習的幾點建議
魏敏
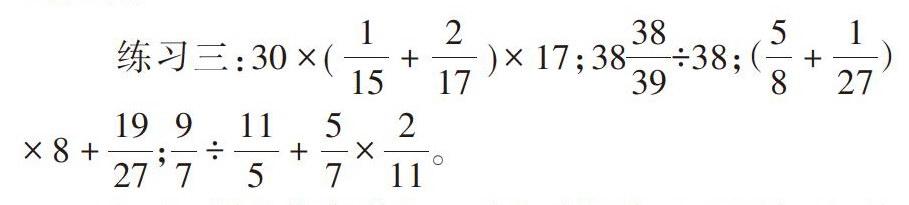

[摘要]、學運算律的學習不僅是為簡算服務,更是為了深化學生對各種運算算理的深刻理解、算法的熟練運用以及厘清加減乘除運算之間的內在關系。這些運算律的相關內容分設在各個年級,復習時只有系統梳理才能融會貫通,促使學生宏觀把握小學四則運算的精髓和要旨。
[關鍵詞]運算律;復習課;建議
[中圖分類號]G623.5 [文獻標識碼]A [文章編號]1007—9068(2019)32—0043—02
復習課的主要功能是鞏固所學舊知,將分散的知識點有機整合起來,形成結構嚴密的系統,促進知識點、線、面的有力結合,它擔負著梳理與回顧、聯通與創新的獨特功能。因此,在復習課中教師要重視整理,力求做到讓學生更好接受、更易理解知識,引導學生從新的站位和視角去審視過去所學的一點一滴,并根據新的目標進行梳理,組織訓練,貫通新舊知識的關系,通過概括、總結,對龐雜的知識進行濃縮,讓學生在完善知識結構的過程中溫故知新,發展數學思維,感悟思想方法,培養數學素養。關于怎樣才能上好復習課,針對不同的課型,做法也不一樣。下面結合小學數學總復習階段對運算律的復習提幾點建議。
一、設計適配學情的教學目標
數學總復習課中,運算律的運用是對整個小學階段計算知識的歸納和整合,讓學生從錯綜復雜的計算中形成簡算、巧算意識并總結出方法。于是,筆者將教學目標進行分解:1.通過整理和復習,構建計算知識網絡,掌握全部的運算律,并能自覺靈活地應用到整數、小數和分數的計算中;2.通過回顧、整理、交流、研究、創新,培養學生認真觀察、精致分析、全面復習的復習模式,感受運算律的實用性和靈活性;3.鞭策學生積極學習簡算技能,養成簡算意識,獲得積極愉悅的情感體驗,并自覺形成“要計算必先簡算”的算術習慣。
如對于乘法分配律應用的設計:
練習一:25×(4+8);125×(40×8);4/5×2/3-2/3×3/5;8.8×125。
練習一旨在要求學生明白乘法分配律適合于整數、小數、分數的計算,并給出類似的算式引導學生區分乘法結合律和乘法分配律。
練習二:1.39×25-0.039×250;4.58×8.6+3.42×8.6;38×99+38;105×(1/7+2/3-1/5)。
練習二旨在要求學生能夠靈活運用乘法分配律使計算變得簡便,變式練習有利于深化學生對乘法分配律的認識。
練習三則是提高學生對乘法分配律的運用意識,并滲透簡算的意識與理論,是對學生計算技能的進一步提高。
三組練習層層遞進,從基本形式到變式訓練再到綜合運用,從簡算形式到簡算技能再到簡算意識,要求逐步提高,學生的思維能力也逐步提升,最終讓學生在計算過程中逐步形成簡算意識。
二、系統整理重構知識體系
復習課的主要特征是“梳理”,即對過往所學的知識進行系統梳理和整合,使之形成縱橫向的聯系,達到以點到面觸類旁通的效果。梳理過程主要包括:
1.回憶運算定律。(1)什么是加法結合律?用語言描述,或用代數式表達。(2)書上還涉及哪些運算定律?兩人為一組,互相補充提醒。要求:①回顧并敘述學過的所有運算律;②嘗試用代數式來表示,或舉出實例來說明。(3)用代數式表示運算律:加法交換律a+b=b+a;乘法交換律a×b=b×a;加法結合律a+b+c=a+(b+c);乘法結合律a×b×c=a×(b×c);乘法分配律(a+b)×c=a×c+b×c,用文字敘述一下乘法分配律的意義。
2.分類整理。(1)對這些運算律有什么看法?用字母表示運算律有什么優勢?式子中的a、b、c可以代表哪些數?(2)為方便觀察識記,你能將這些運算律進行分類嗎?(3)根據運算符號分類,你覺得哪個運算律最特殊?理由是什么?
3.舉例驗證。你能詳細解釋分配律的意義嗎?嘗試通過實例來揭示分配律的奧秘。如“小強每天完成70個字的書法練習,3月份上旬堅持了5天,中旬堅持了9天,3月份中旬比上旬多寫幾個字?”舉出實例來驗證運算律的正確性,不失為一個巧妙高效的復習方法。
三、分層練習稀釋難度
復習課應“兜底、不限高”,讓不同層次的學生都能有所獲,為此,筆者設計了三組練習題。
練習一:說一說,下面哪幾題可以簡算?具體怎么操作?理論基礎是什么?
讓學生回憶四則混合計算的一般方法。
練習二:將題目補充完整,使它們具備簡算的特性。
練習三:具備簡算條件的請簡算。
運用的運算律不同,拆分的方式也就有所區別,但在此過程中什么是一致的?那就是所有的變形都是等價的,不能改變最終的計算結果。計算時,要求學生敏銳捕捉算式中的數字特點和運算符號之間的內在關系,并通過合并分解等手段,靈活運用運算律解題。
四、加強運用提高實用性
數學取之于生活,用之于生活,數學學習的價值在于運用。因此總復習時,教師應立足長遠,高屋建瓴,挑選“客觀的、有意義的、貼近生活的”素材,精心設計練習題,讓學生在探究生活問題和應用數學知識解決問題時,開闊思路,擴大視野。
如機床上有一塊鋁片零件(如圖1),這塊鋁片零件的面積有多少平方厘米?(1)不同的方法:5.18×2.1+4.82×2.1;(5.18+4.82)×2.1。(2)你這樣做的理由是什么?(3)課件演示。求幾何面積也可以使用運算律,主要是運用相同元素的拆分與合并來簡化計算。
復習也要接地氣,不要曲高和寡,脫離現實,同時復習也不能炒冷飯,復習題的內容、題型要不斷推陳出新,不要老是“重復昨天的故事”,要輸入新鮮血液和養分。
如圖2,兩個正方形之間涂色部位的面積為100平方厘米,求圓環的面積。
最后就是總結提升:“今天我們整理復習了運算律,你有哪些收獲?提取了哪些信息?”讓學生暢所欲言,使學生的認知水平不斷提高,為今后的學習奠定基礎。
(責編 羅艷)

