基于MEMS-MARG傳感器的消防員室內定位算法

楊 剛，李 強，韓 路，張 鑫

（西安郵電大學 通信與信息工程學院，西安 710121）

常年以來，建筑物火災事故頻有發生，常需要消防員進入火場進行滅火和救援。火場環境煙霧彌漫，能見度低，消防員難以確定自己的具體位置，給滅火和救援帶來了很大的困難。由于缺乏成熟的消防員室內定位系統，不僅影響了消防員的救援效率，也極大威脅到消防員的生命安全，造成更大悲劇的發生。

目前關于消防員室內定位算法的研究成果比較少，主要以UWB、RFID、ZigBee、WIFI、慣性導航等方面的定位算法研究為主。文獻[1]使用UWB技術實現消防員火場定位，UWB雖然具有較高的定位精度，但是需要提前部署定位基站，并且在室內環境中易受遮擋造成較大的非視距誤差。文獻[2]使用RFID技術定位，這種方式雖然成本低，但是其抗干擾能力較差。文獻[3]使用基于RSSI算法的ZigBee技術實現消防員室內定位，這種定位方式雖然功耗小，但是易受多徑效應的影響。上述定位技術具有一定的局限性，在真實火場環境中很難滿足消防員精確實時定位的需求。

慣性導航定位技術是一種不依賴任何外部設備或先驗數據庫，自主性強的室內定位技術[4]，比較適合于消防員在火場中的定位。隨著MEMS技術的發展，慣性傳感器的體積變得越來越小，成本逐漸降低，被大量用于行人導航系統中[5]。9軸MARG（Magnetic,Angular Rate,and Gravity）系統，是一種包含3軸加速度計，陀螺儀和磁力計的傳感器陣列，能夠提供相對于重力方向和地球磁場方向的完整測量[6]。行人航跡推算（Pedestrian Dead Reckoning，PDR）算法基于行人步態的運動生理學特征，利用慣性傳感器計算行走時的步數、步長和航向信息，由初始位置推算出行人的位置坐標[7-8]。

本文使用MARG系統作為定位數據采集的終端，根據消防員行走過程中所采集的3軸加速度值、3軸角速度值和3軸磁強度值，計算出步數、步長和航向角信息，使用PDR算法結合擴展卡爾曼濾波器（Extended Kalman Filter,EKF）估計出消防員的位置坐標。對于步數檢測問題，設計了一種根據加速度幅值波形使用峰值探測法和零點交叉法相結合的方式進行步數檢測；對于航向角誤差的累積問題，在改進的啟發式漂移消除（improve Heuristic Drift Elimination,iHDE）算法[9]的基礎上設計了一種航向反饋修正算法，通過直行判定和主導方向判定將消防員的行走狀態進行嚴格分類，對每種狀態采取不同的航向修正措施。最后，將EKF和PDR算法融合，推算出消防員的行走軌跡。通過上述方法，可以有效地提高消防員在室內環境中的定位精度。

1 系統介紹

定位系統的算法框架如圖1所示。首先通過消防員胸前佩戴的傳感器獲取行走過程 MARG系統的原始數據，對原始數據進行濾波和校準預處理。對預處理后的數據分別進行以下處理：使用Madgwick算法根據3軸加速度、角速度和磁場強度求出航向角；通過加速度幅值來獲取行走步數和步長信息；對獲取的原始航向角進行濾波預處理，再經過反饋修正算法修正航向；最后通過PDR算法根據步數、步長和航向數據使用EKF估計出消防員的位置坐標。

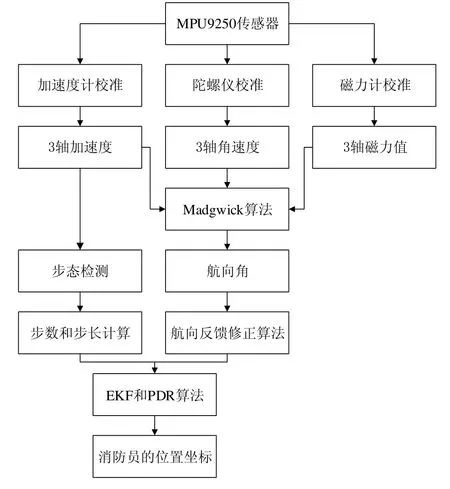
圖1 系統框架Fig.1 System framework

2 消防員室內定位算法

2.1 坐標系

本文采用的導航坐標系（n系）是東北天（East North Up，ENU）坐標系，X、Y、Z軸分別為正東、正北和法線方向，構成右手坐標系。載體坐標系（b系）是用戶自身所定義的坐標系，原點是導航設備的中心，消防員行走中水平前進方向為Y軸，設備的右側為Y軸，Z軸垂直向上。

在 ENU坐標系下，通過下文介紹的步數檢測、步長計算和航向求解及修正使用PDR算法結合EKF計算出消防員的位置坐標。

2.2 步數檢測

傳統的步頻檢測法有峰值檢測法[10]、零點交叉法、自相關法、快速傅里葉變換法等[11]。考慮到消防員在火場行走的復雜情況，本文通過對加速度幅值的波形分析，使用峰值探測法和零點交叉法結合的方式進行步數檢測，具體過程如下所述。

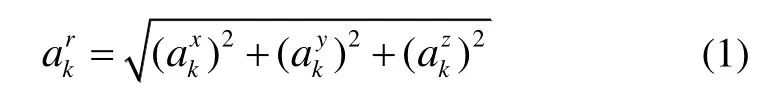
其次將傳感器靜止放置一定的時間進行加速度數據采樣，計算出本地的重力加速度值。將減去的加速度幅值進行Kalman濾波：

狀態方程為：

式中，ak為k時刻Kalman濾波的狀態變量，預測噪聲滿足由具體實驗環境決定。

觀測方程為：

再對經過 Kalman濾波后的結果進行平滑濾波，經過處理后的加速度幅值波形變得更加平滑，如圖2所示，這時可以進行步數檢測。預設加速度閾值和相鄰波峰時間閾值來檢測加速度波峰，根據波峰數來確定消防員行走步數M；通過加速度幅值波形零點特征，判斷加速度幅值前一點小于 0，當前點大于或等于 0，并且預設相鄰零點時間閾值來檢測零點，準確標記一步的開始時刻和結束時刻，用于獲取一步之內加速度的最大值和最小值來計算步長。根據零點交叉算法標定的每一步開始與結束時刻，求出每一步的航向角平均值，作為下文航向角修正的原始航向角。圖2中紅色五角星標記為檢測到的波峰，綠色圓圈標記為檢測到的零點。

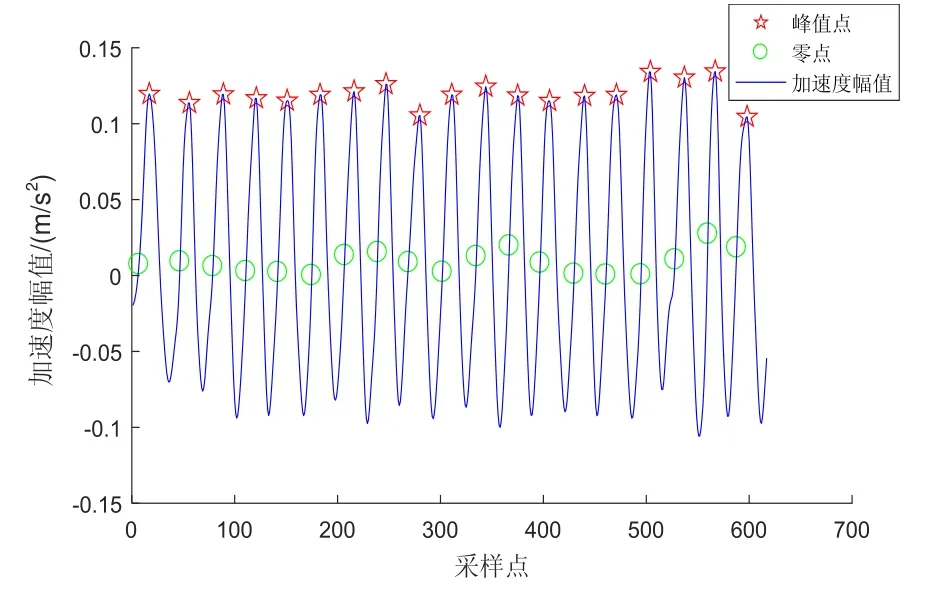
圖2 加速度幅值波形Fig.2 Acceleration amplitude waveform

2.3 步長估計

本文根據加速度幅值信息使用非線性步長模型[12]來計算消防員行走過程中每一步的步長：

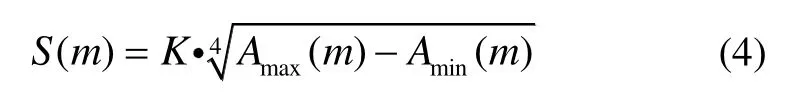
式中，K是模型參數，Amax(m)和Amin(m)代表第m步加速度的最大值和最小值，S(m)表示第m步的步長。

2.4 航向角求解

本文將9軸MARG傳感器輸出的3軸加速度值、3軸角速率值和3軸磁力值通過Madgwick算法[6]更新四元數來求解航向角。

Madgwick算法的目標是通過加權融合k時刻的陀螺儀算出的四元數和加速度計與磁力計共同計算出的四元數，進而得到最優的四元數融合加權的公式如下所示：

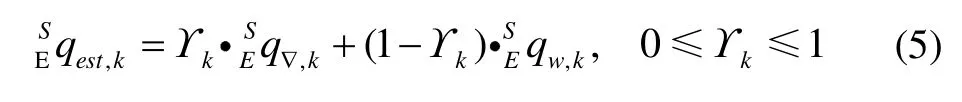
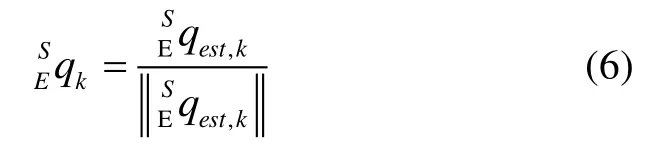
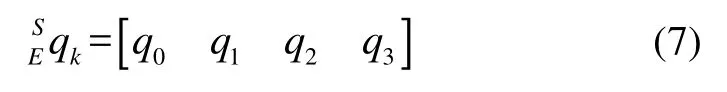
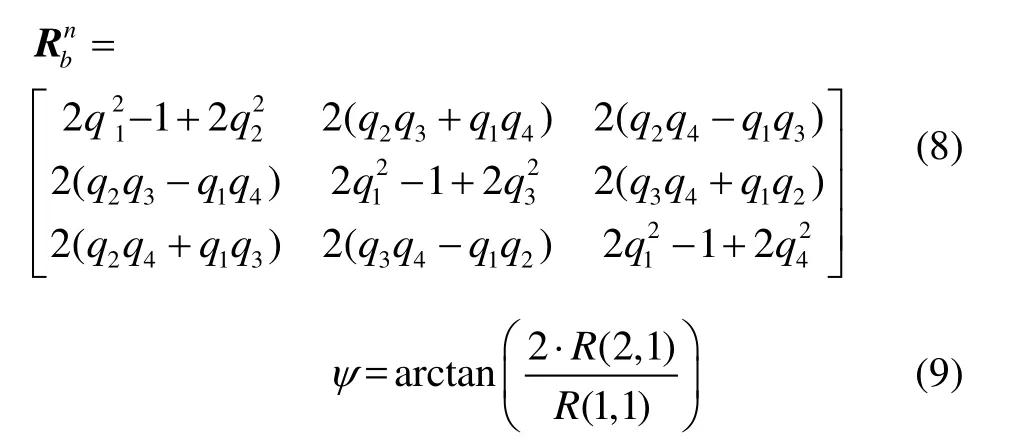
2.5 航向反饋修正算法

本文提出的航向反饋修正算法通過直行判定和主導方向判定將消防員的行走狀態進行嚴格分類，對于每種狀態采取不同的航向修正措施，避免出現錯誤矯正情況的發生，增加了算法的健壯性。此外，用于航向修正的卡爾曼濾波器狀態變量只有一維，減少了算法的復雜度和運算成本。

本算法將消防員在室內行走路線分為兩類，分別是曲線行走和直線行走。曲線行走時算法不直接修正航向角，由于算法框架融合的磁力計保證了原始航向角具有一定的精確度，所以可以直接使用原始航向角進行坐標計算。直線行走又分為沿著主導方向直線行走和沿著非主導方向直線行走。在主導方向直線行走時使用主導方向值作為航向角參考值，在非主導方向直線行走時使用鄰近三步航向角的均值作為航向角參考值，將當前航向角與航向角參考值的差值作為卡爾曼濾波器的觀測量，求出最優航向誤差估計值，使用當前航向減去最優航向誤差估計值得到修正后的航向角。

算法的具體流程如圖3所示。首先對原始航向角進行濾波預處理，然后進行直行判斷和主導方向判斷，再計算航向角偏差，最后對航向角偏差進行卡爾曼濾波處理，進而修正航向角。算法詳細步驟如下所述：

到了24周，寶寶體重約650克，4周時間里從20周的300克又增重了350克，平均每周增重90克左右。這時會發現寶寶增重加快了，從16～20周每周的45克到每周90克。相對而言孕媽媽也應該開始增加增重幅度了，每周應該在250克左右，這樣到24周，孕媽媽從孕前開始可以增重4千克左右。其中大約2.5千克是必需增重的，1.5千克是為將來母乳喂養寶寶做準備的。

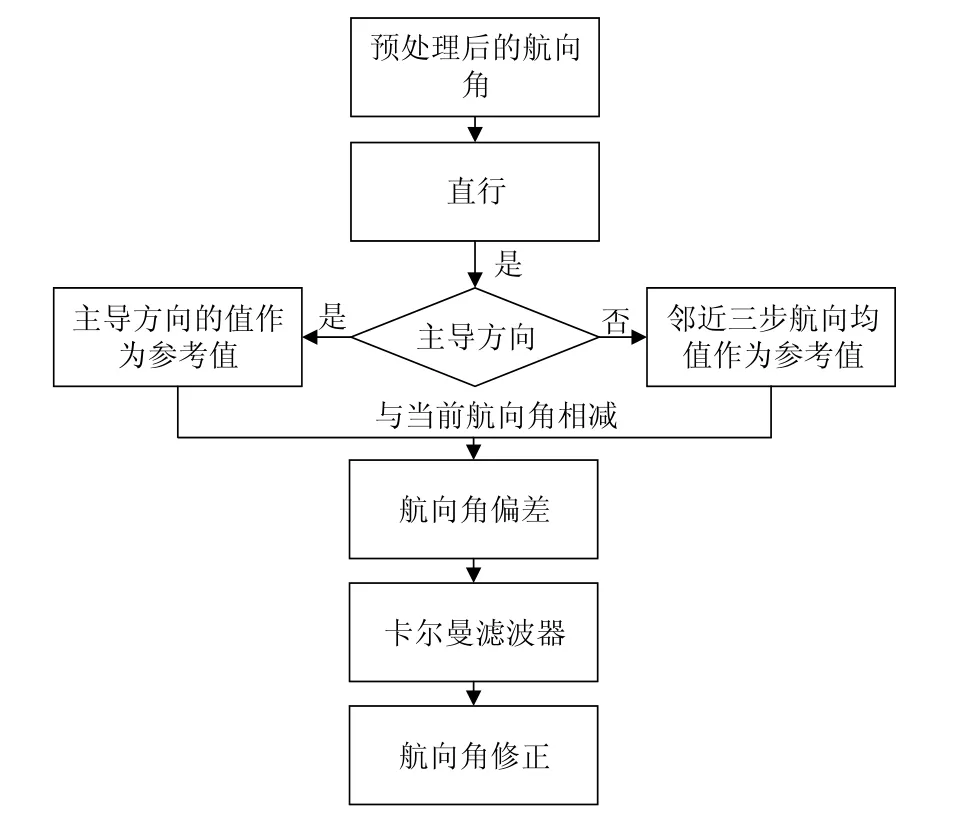
圖3 航向反饋修正算法流程圖Fig.3 Flow chart of heading feedback algorithm

1）主導方向設定

根據建筑物大多坐南朝北的特點，本文設置了東、西、南、北4個主導方向，如圖4所示，主導方向之間的間隔Δ是90°。本文設定航向角的范圍是 0°到±180°。

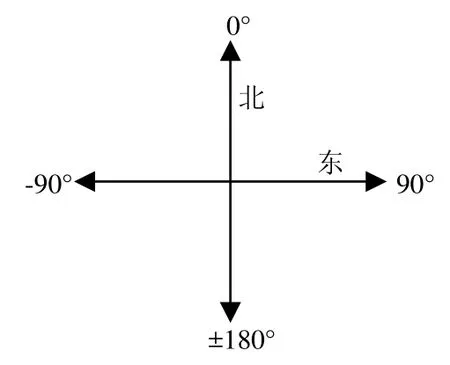
圖4 主導方向Fig.4 Dominant direction

2）直行判定

分別用連續 3步航向值減去這三步航向的平均值，并獲取最大航向差值和預設的閾值進行比較，如式(10)所示：

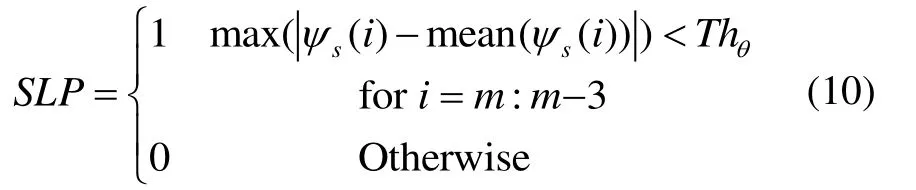
式中，m為當前時刻的步數。

當SLP為1時判定為直線行走，可以進入下一項判斷；當SLP為0時判定為非直線行走，不進入下一項判定。Thθ為直線行走判定預設的角度閾值。

3）主導方向判斷

在判定為直線行走的條件下，使用MOD函數來判斷消防員是否在主導方向直行：

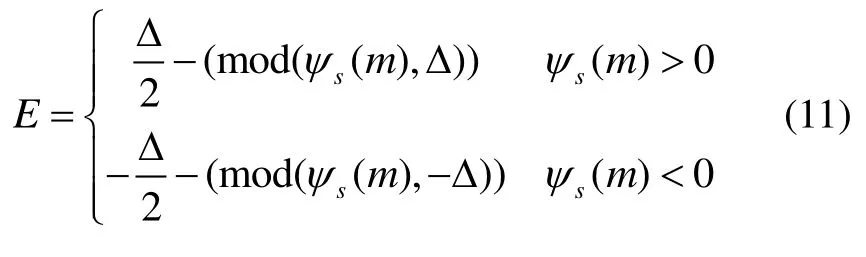
當E的絕對值大于35°時，判定為主導方向行走；當E＞0時，行人在鄰近主導方向的右側，當E＜0時，行人在鄰近主導方向的左側。E的閾值設定是參考相關文獻[9,13-14]，并經過大量實驗確定的。

4）航向角誤差計算

在主導方向直行時，航向角誤差值δψ(m)等于當前航向角ψs減去鄰近主導方向的值；在非主導方向直行時，航向角誤差值δψ(m)等于當前航向角減去鄰近三步航向角的均值，即：

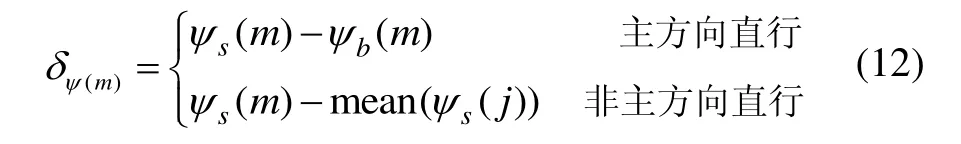
式中：ψb為與當前航向角ψs最鄰近的主導方向的航向值；mean(ψs(j))為鄰近三步航向角的均值，j=m,m-1,m-2；δψ(m)作為卡爾曼濾波器的觀測量用來修正航向角。

5）航向角誤差置信度

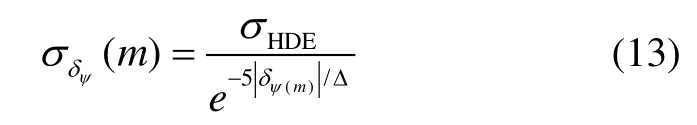
式中，σHDE=0.1 rad[9]。在對航向角誤差δψ(m)進行Kalman濾波時，將σδψ(m)作為觀測噪聲大小的參考值。

6）卡爾曼濾波處理

本文使用航向角誤差值δψ(m)作為Kalman的觀測量來估計出最優航向角誤差X(m|m)。卡爾曼濾波算法的詳細過程可以參考文獻[13]，本文不再贅述。

7）航向角修正

根據 Kalman濾波器求出的最優航向角誤差估計X(m|m)，使用當前航向值ψs(m)減去最優航向誤差估計值X(m|m)得到修正后的航向值(m)，即：

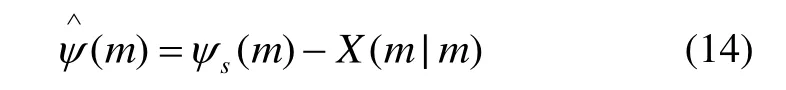
式中，ψs(m)為修正前的航向角，(m)為修正后的航向角。

2.6 消防員行走軌跡推算

本文將擴展卡爾曼濾波器（EKF）和PDR算法融合，把前文獲取到的步數m、步長S(m)、和修正后的航向角(m)代入到EKF中推算出消防員的最優行走軌跡。具體過程如下所述：

系統狀態變量為：

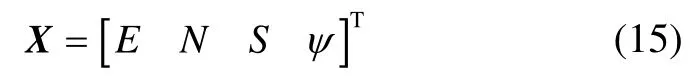
式中，E和N為消防員在ENU坐標系中的東向和北向坐標，S為每一步的步長，ψ為每一步的航向角。

根據PDR算法，狀態方程為：

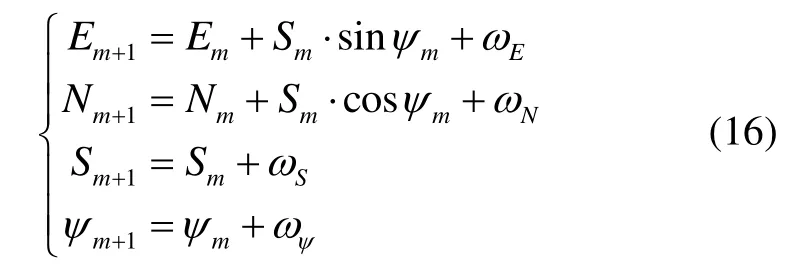
由于狀態方程(16)是非線性方程，根據EKF的原理，用狀態方程計算的雅各比矩陣近似表示狀態轉移矩陣：

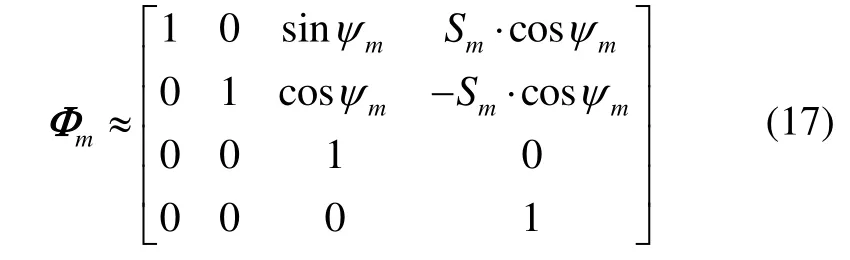
動態預測噪聲為：

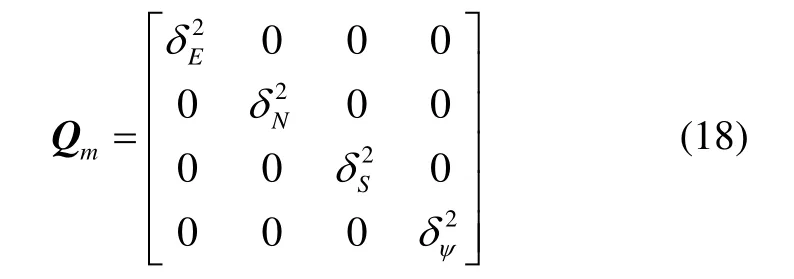
觀測量為：

觀測方程為：

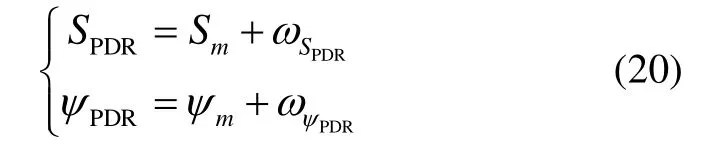
觀測方程是線性方程，觀測矩陣為：

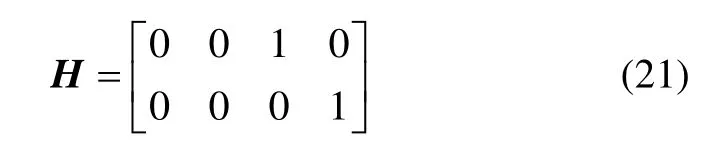
觀測噪聲矩陣為：

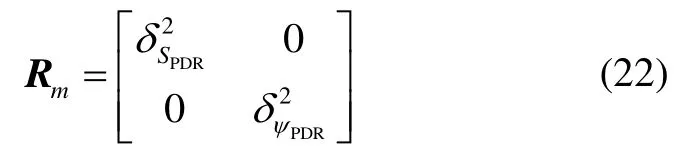
通過EKF的預測更新和測量更新動態方程，可以得到狀態變量的最優估計值：

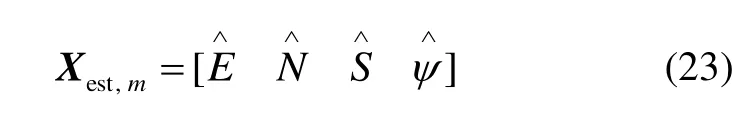
3 實驗驗證與分析

3.1 數據采集

本次實驗使用集成MPU9250傳感器的JY901作為實驗數據采集平臺。JY901的主控部分STM32F051是一款基于ARM 32-bit的Cortex?-M0 CPU，具有32k到64k字節的Flash Memory，工作頻率高，功耗低，外設豐富且價格低。MPU9250是一款9軸MARG運動跟蹤傳感器，由3軸加速度計、3軸陀螺儀和3軸磁力計組成。加速度計誤差為±6mg，陀螺儀誤差為±5 (°)/s。經過測試，根據MPU9250傳感器采集的慣性數據，使用 Madgwick算法求取的原始航向角誤差在±10°范圍內波動。在實驗中，設定傳感器的數據采集速率是50 Hz，工作電壓是3.3 V，波特率為115 200 Hz。實驗場地是西安郵電大學東區逸夫樓八樓自習室，實驗中慣性傳感器佩戴在測試人員胸前，傳感器獲取到的數據通過串口傳輸到PC端，由Matlab軟件來處理數據，如圖5所示。

圖5 數據采集Fig.5 Data acquisition

3.2 實驗內容

為了驗證本文提出的消防員室內定位算法的性能，設計了3組實驗，測試人員胸前佩戴著傳感器，分別沿著矩形路線、三角形路線和半圓形路線進行實地測試。

1）矩形路線實驗

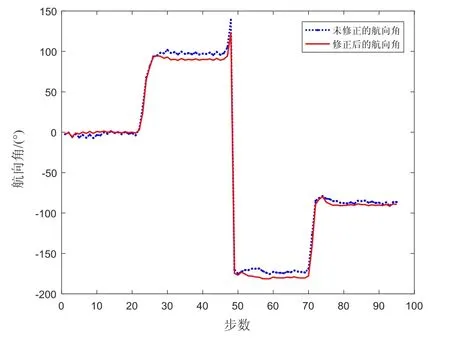
圖6 矩形實驗航向角變化Fig.6 Variations of heading angle inrectangular experiment

矩形路線實驗是沿著東、南、西、北四個主導方向行走一圈，以驗證在這四個主導方向上直行時航向反饋修正算法的性能。圖6是測試人員行走過程中航向角的變化，通過對比分析，未經修正的原始航向角波形不平整且偏離真實值，經過航向反饋修正算法處理的航向角更加平滑并且較為接近真實航向值。圖7為矩形實驗的行走軌跡，無航向修正的PDR算法軌跡圖在短時間嚴重偏離真實軌跡，加了航向反饋修正算法的軌跡圖始終接近真實軌跡。

如表1所示，使用的航向反饋修正算法的返回原位置誤差（Return Position Error,RPE）為0.9048 m，與未使用相比提升了46.84%，位置RMSE提升了77.90%，航向 RMSE提升了 65.03%。本次實驗驗證了在主導方向直行時航向反饋修正算法可以很好地修正航向。

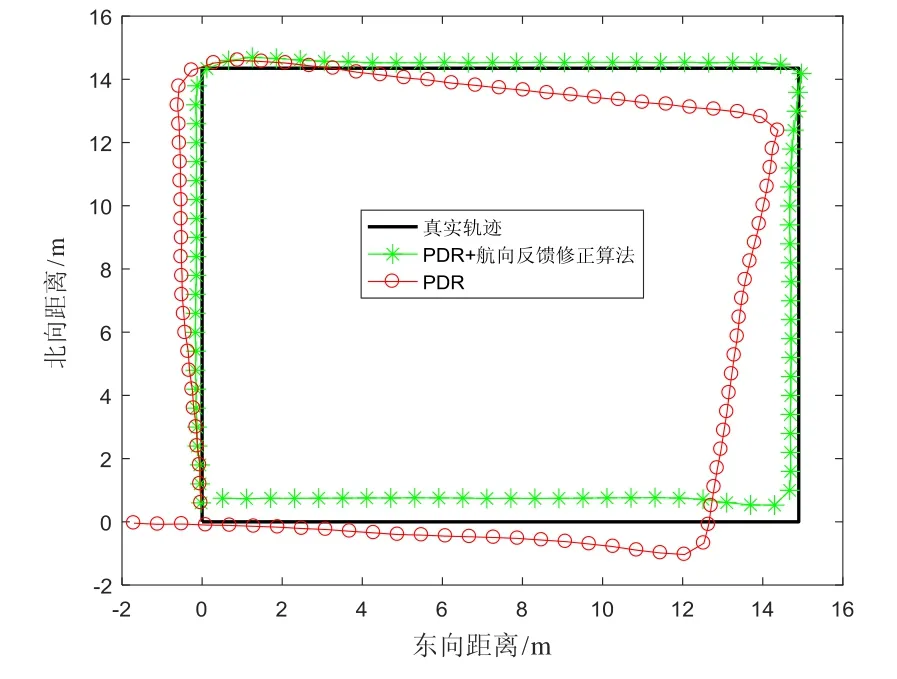
圖7 矩形實驗行走軌跡Fig.7 Rectangular experimental walking track

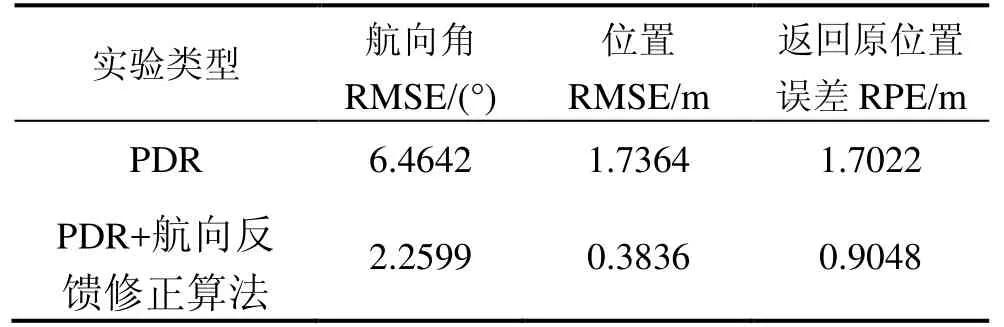
表1 矩形實驗精度分析Tab.1 Accuracy analysis of rectangular experiment

2）三角形路線實驗

在三角形路線實驗中，行走軌跡為一個直角三角形，兩條直角邊在主導方向上，一條斜邊在非主導方向上。該實驗是為了驗證在非主導方向直行時，航向反饋修正算法的性能。圖8為航向角變化情況，其中前兩段為在主導方向直行時的航向角變化，最后一段為在非主導方向直行時的航向角變化。圖9為三角形實驗的行走軌跡，相比單純使用PDR算法，添加了航向反饋修正算法生成的軌跡更加接近真實軌跡。

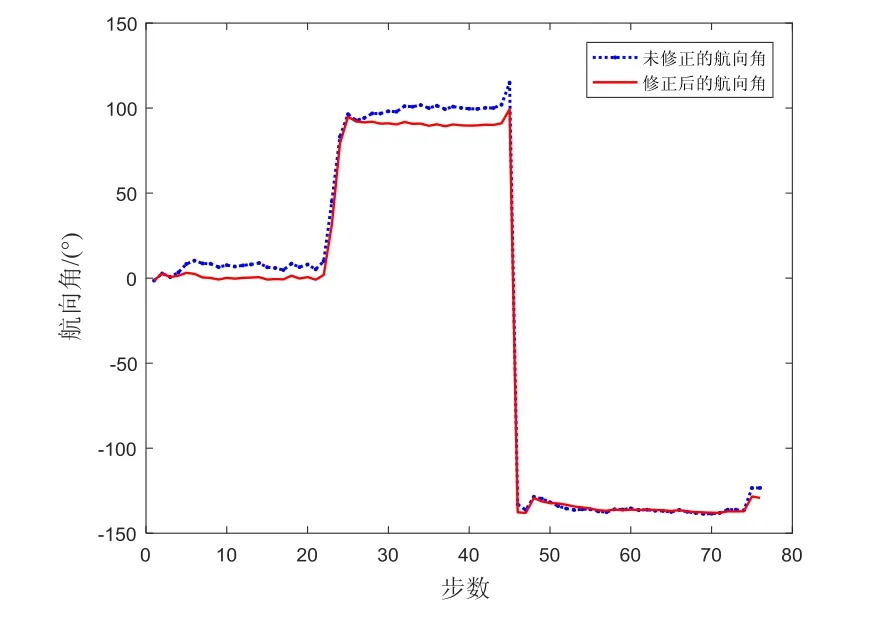
圖8 三角形實驗航向角變化Fig.8 Variations of heading angle in triangular experiment

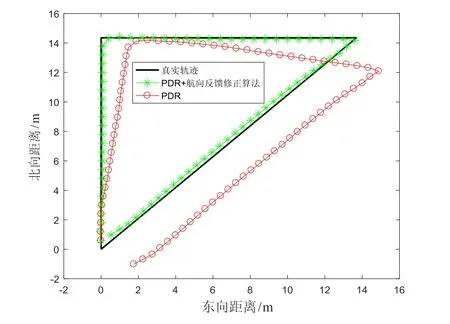
圖9 三角形實驗行走軌跡Fig.9 Triangle experimental walking track

如表2所示，添加的航向反饋修正算法 RPE為1.10m，與未使用航向修正算法相比提升了 45.54%，位置 RMSE提升了 76.81%，航向 RMSE提升了68.21%。三角形實驗的結果表明在非主導方向直行時航向反饋修正算法具有良好的精度。

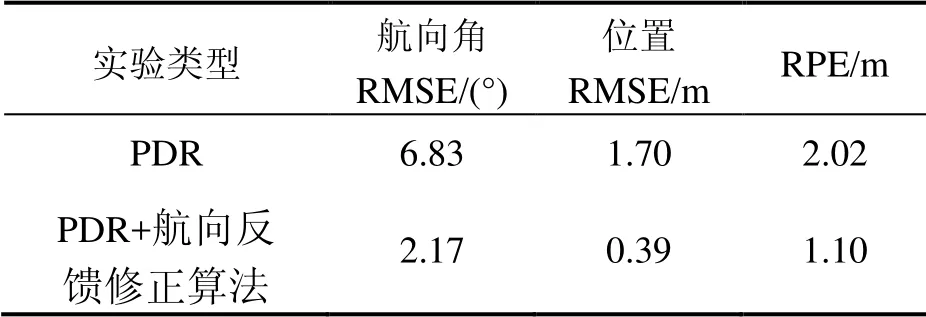
表2 三角形實驗精度分析Tab.2 Accuracy analysis of triangle experiment

3）半圓形路線實驗

半圓形路線實驗設定為直徑在主導方向上，圓弧在非主導方向上，這是對航向反饋修正算法設計的挑戰性實驗。半圓形路線實驗的航向角變化如圖10所示：第一段是沿著直徑在主導方向上直行，航向反饋修正算法會修正航向角；第二段是沿著圓弧曲線行走，由于實際航向角在不斷變化，相比于直線行走，沒有一個固定的航向角觀測值，導致難以計算出航向角偏差，無法對航向角進行直接修正，航向反饋修正算法性能會暫時下降，軌跡推算直接使用原始航向角。實驗軌跡如圖11所示，由于真實行走軌跡的半圓不是規則的半圓，是一個近似的半圓，所以在本實驗的軌跡圖中并沒有標出真實的軌跡。本文提出的航向反饋修正算法框架融合了磁力計，求出的原始航向角具有一定的精確度，在曲線行走航向修正算法性能下降的情況下，如圖11所示，所依據的原始航向信息依然具備一定的準確性。考慮到在多數情況下人的行走是直線行走，所以在曲線行走時導致短暫的算法性能下降不會對最終定位精度產生較大的影響。

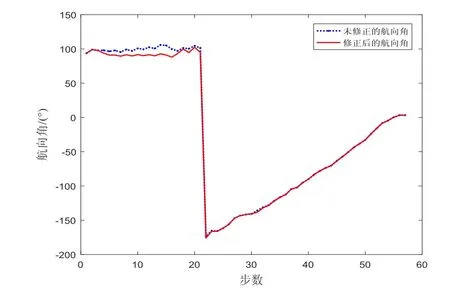
圖10 半圓形實驗航向角變化Fig.10 Variations of heading angle in semicircular experiment

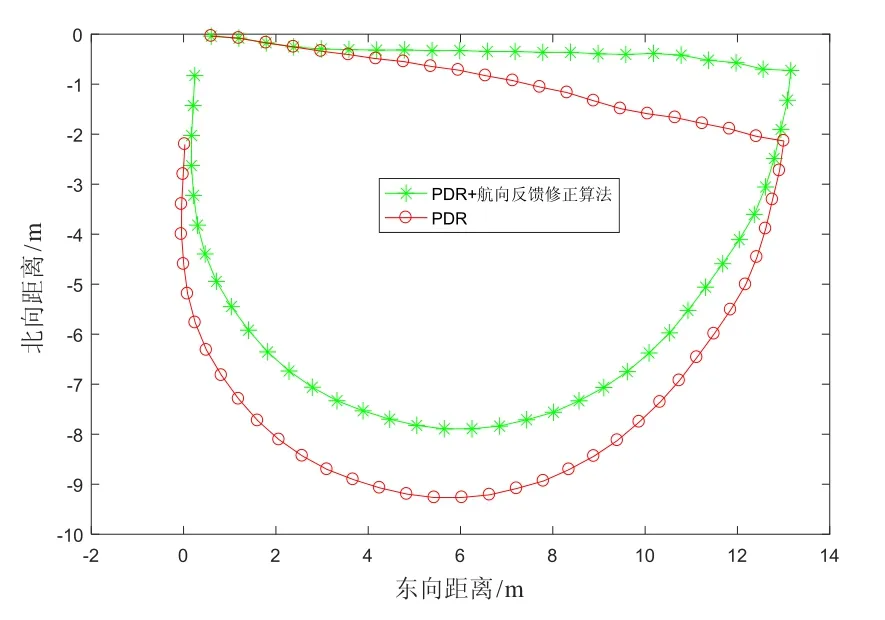
圖11 半圓形實驗行走軌跡Fig.11 Semicircular experimental walking track

4 結 論

本文以MARG傳感器為基礎，針對消防員室內火場定位的應用背景，設計了一種導航定位方法。針對PDR算法中的步數檢測問題，設計了一種根據加速度幅值波形使用峰值探測法和零點交叉法相結合的方法來準確獲取消防員的行走步數。針對慣性導航中航向角誤差隨時間和行走距離增大的問題，提出了一種航向反饋修正算法來修正航向角。當消防員沿著直線路徑行走時，算法會對航向角進行修正，修正后的航向角結合步數和步長信息通過EKF和PDR算法來估計出消防員的位置坐標。算法框架所融合的磁力計增加了航向信息的準確度，即使消防員在非理想路徑行走時也可以獲得良好的定位精度。綜合3組實驗，本文所提算法將 RPE提升了 45%以上，航向角和位置的RMSE分別提升65%和76%以上，具有較好的穩定性和可靠性，能適應較為復雜的應用場景。

本文所述的定位方法為消防員在室內火場環境中的位置信息獲取提供了一種有效的解決方案。在后續的研究中，將考慮如何解決周圍磁場環境對磁力計測量精度的影響。磁力計擾動的改善將有助于提高定位精度，進而保障消防員的自身安全和提高救援效率。