函數的最值問題在實際問題中的應用研究

陳影影

（上海電機學院文理學院，上海 201306）

解決現實生活中一些問題，例如：在一定條件下，如何使“材料最省”“利潤最大”“成本最低”等，想要解決這類問題，可以通過研究各個變量之間的關系，建立相應的函數關系式，并進一步研究該關系式的最值問題。函數的最值問題在多個科學領域中都有很廣泛的應用，這就需要把實際遇到的問題，抽象成各個變量之間的函數關系，并進一步轉化成微積分學里的求最值問題來解決，所以，對函數最值問題以及對最值問題應用的研究有著非常重要的意義。

1 最值定理

如果函f（x）在區間[a，b]上連續，那么f（x）在[a，b]上一定能夠取到最大值和最小值。

如圖1所示，定理1 說明，如果函數f（x）在閉區間[a，b]上連續，那么至少有一點x1∈[a，b]，使f(x1)是f(x)在[a，b]上的最大值，即對一切x∈[a，b]，均有f（x1）≥f（x）成立；又至少有一點x2[a，b]，使f(x2)是f(x)在[a，b]上的最小值，即對一切x∈[a，b]，均有f（x2）≤f（x）成立。

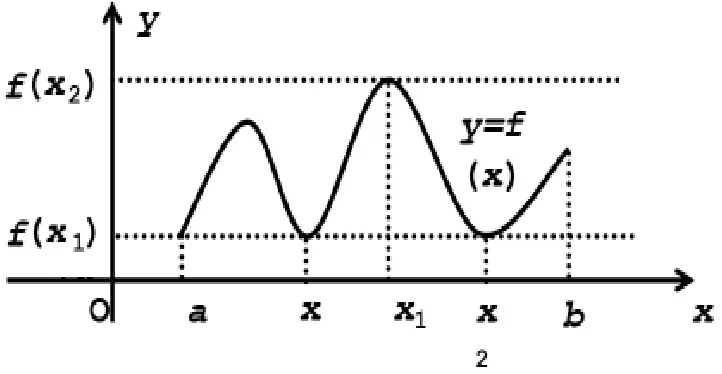
圖1 函數圖

2 方法步驟

對于閉區間上連續的函數f（x）來說，其最大值和最小值一定存在。如果最大值或最小值在區間（a，b）內部取得，那么它一定也是極值，而極值只可能在f（x）的駐點或導數不存在的點取得。當然最大值或最小值也有可能在區間的端點出取得，這時最大值或最小值就不一定是極值。因此，求函數f（x）在[a，b]上的最值（最大值或最小值）的方法與步驟如下。

（1）求出f（x）所有可能極值點的函數值，并將這些函數值與端點處的函數值f（a），f（b）做比較，比較之后這些值中所得到的最大值就是所求的最大值，所得到的最小值就是所求的最小值。

（2）對于閉區間[a，b]上的連續函數f（x）來說，倘若在這個區間的內部只有唯一的一個可能的極值點，并且f（x）在這一點的確存在極值，那么，這個唯一的極值點就是所求的函數在[a，b]上的最值點。

實際問題求最值應注意如下內容。

（1）建立目標函數；（2）求最值。

若目標函數只有唯一駐點，則該點的函數值即為所求的最大值（或最小值）。

3 應用舉例

3.1 最值問題在物理學中的應用

函數最值問題也經常被用來解決物理學中的一些問題。

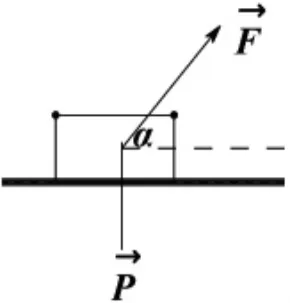
圖2 最值問題在物理學中的應用

令φ（α）=cosα+μsinα，

則問題轉化為求φ（α）的最大值問題。

φ'（α）=-sinα+μcosα，α"（α）=-cosα-μsinα，

令φ'（α）=0，解得α=arctan μ=arctan 0.25=14°2'，而φ"（α）＜0，所以α=14°2' 時φ（α）取最大值，因而取最小值。

最值問題在經濟活動中也有非常廣泛的應用，以下舉例說明。

3.2 費用最省

例：公路上A，B 兩點間的長度是100 km，點C 和A 為20 km，AC⊥AB，現在要在A，B 兩點之間確定一點D，在D 和C 之間修一條新公路，已知公路AB 與公路CD 每公里貨運價之比為3∶5，把貨物從B 處運到C處，問D 點應該如何確定才能使總運費最省(見圖3)?

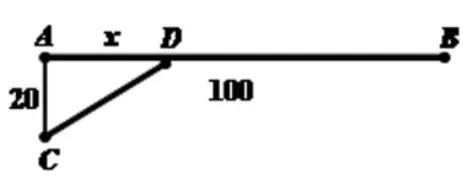
圖3 費用最省問題圖

3.3 利潤最大

例：一工廠生產x 千件某種產品的成本是C（x）=x3-6x2+15x，而賣出這種產品的收入是R（x）=9x，問該工廠該如何生產才能使利潤最大(見圖4)？

圖4 利潤最大問題圖

解：售出x 千件產品所得的利潤表達式為

p（x）=R（x）-C（x）=-x3+6x2-6x，

兩端求導得

p'（x）=-3x2+12x2-6=-3（x2-4x+2）。

3.4 經濟批量問題

例:一個商場每年賣出某種商品a 件，共分為x 次進行批貨。每次批貨的費用為b 元，而沒能及時賣出的商品需庫存，庫存的費用為c 元/（年·件）。假設賣出商品是均勻的，問分多少批進貨時，才能使以上兩種費用的綜合為最省？ （a，b，c 為常數且a，b，c>0）

解：根據題意，x 次批貨的總費用為

W1（x）=bx。

3.5 梁的抗彎截模量最大

例：把一根原木用鋸鋸成矩形的梁，原木的直徑為，為了使矩形梁的抗彎截面模量達到最大，問應如何確定矩形截面的長和寬（見圖5）？

解：設矩形截面的長為h，寬為b。由力學知識知，梁的抗彎截面模量為

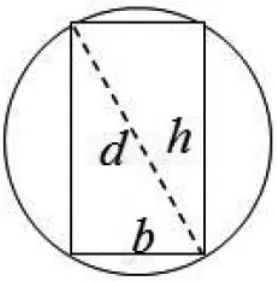
圖5 梁的抗彎截面模量最大問題圖

由題意知，當時，可以使矩形梁的抗彎截面模量達到最大。

3.6 用料最省

例：設計固定體積圓柱形飲料罐，罐的側面和底部是用整塊材料制成的，頂部蓋子的厚度是側面或底部的三倍，為了使總用料最省，應如何設計它的底面半徑r 和高度h？

解：飲料罐的體積記為V，設飲料罐身的側面和底部厚度均為δ，那么頂蓋的厚度是3δ，高

所以，飲料罐側面和底部總用料為U1（r）=δ（πr2+2πrh）=δ（πr2+），

頂蓋的用料為U2（r）=3δπr2，因此問題轉化為求函數

U（r）=U1（r）+U1（r）=δ（4πr2+），r∈（0，+∞）的最小值。

所以r0是U（r）的最小值點。這時相應的高為

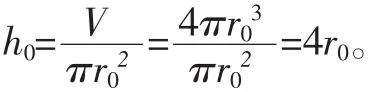
即，當h=2r 時，用料最省。

4 結語

文章對最值定理及最值的計算方法做了簡單的介紹。不僅舉例說明了最值問題在物理計算中的應用，也分類討論了在經濟學領域里對最值定理及計算方法的應用。由此可知，在解決實際問題時對函數最值問題的應用非常的廣泛。