星箭連接界面處環形分布動載荷識別

尹 健，吳邵慶，陳樹海

(1. 東南大學工程力學系，南京 210096；2. 東南大學空天機械動力學研究所，南京 211189；3. 上海衛星工程研究所，上海 201109)

0 引 言

衛星等航天器所受到的動態載荷信息是其結構設計的關鍵，獲取精確的動態載荷在航天工程實踐與研究中具有重要的意義。火箭與衛星之間常采用包帶連接結構，其連接性能將影響星箭系統的動力學特性，因此星箭連接動力學問題受到廣泛關注[1]。火箭發射過程中會受到橫向載荷的作用，在星箭連接界面上產生彎矩和剪力，使得星箭連接處的動載荷呈現環形且非均勻分布的特征。由于技術與成本限制，往往難以通過直接測量獲取動載荷信息。而動載荷間接識別技術可以作為星箭界面動載荷獲取的手段，即利用可以準確測量獲取的衛星結構動響應來反演衛星結構所受的環形分布動載荷。

根據動載荷的特征，動載荷識別方法可以劃分為集中動載荷識別方法和分布動載荷識別方法。集中動載荷識別方法主要包括頻域法和時域法。頻域法是基于離散物理空間或者模態空間內的結構動力學方程，在頻域內根據系統的頻率響應函數與響應頻譜之間的關系來識別動態載荷[2-3]。頻域法要求測量數據的樣本具有一定的長度，故一般只適用于穩態或平穩隨機動載荷的識別，對瞬態沖擊或非平穩隨機動載荷的識別有較大局限性。與頻域方法相比，時域法在考慮時變特征等方面具有一定的優勢，其反求結果精度較高[4]。經典時域法是在模態空間內利用杜哈梅積分構建響應與載荷的關系，反演動態載荷；在此基礎上，進一步發展了基于正交基模型的識別方法[5-6]等。Wu和Law[7-8]則對不確定性動載荷的識別進行了研究。作為反問題，動載荷識別存在不適定性的問題，針對此問題，在經典的Tikhonov正則化方法的基礎上，Qiao等[9]提出了基于稀疏反卷積模型的PDIPM(Primal-Dual Interior Point Method)法，對沖擊載荷進行了識別。近年來，不少學者將動載荷識別方法應用于飛行器的動彎矩識別中[10-11],為飛行器設計提供了寶貴的載荷信息。

對于分布動載荷，雖然其識別方法與集中動載荷識別方法有相通之處，但由于要同時獲取動載荷的空間分布形式以及隨時間變化的規律，其識別難度較大。秦遠田等[12]提出了基于廣義正交多項式的分布動載荷識別方法，并將該方法應用于梁板結構的分布動載荷識別；Jiang和Hu[13]基于Legendre多項式對動載荷的空間分布函數進行正交展開，對薄板上的分布動載荷進行了識別。Li等[14]基于分布動載荷的空間分布與時間歷程可解耦的假設，利用脈沖響應函數與Chebyshev正交多項式對分布動載荷進行了識別。

目前，識別分布動載荷的思路一般是基于集中動載荷的識別方法，通過引入正交基函數來擬合動載荷的空間分布，將連續分布的動載荷識別問題降階為有限個參數的識別問題。但仍然存在以下問題：首先，在動載荷分布特征未知的情況下，擬合空間分布函數的正交多項式階數難以確定；其次，正交基函數是一種全局基函數，針對具有局部突變分布特征的動載荷難以精確識別；最后，對于具有周期性特征的環形分布動載荷，用正交多項式來擬合動載荷的空間分布，無法保證環形動載荷分布的首尾連續性，亦不能保證動載荷分布函數導數的連續性。為改進基于正交多項式的分布動載荷識別方法存在的問題，本文提出基于B樣條基函數的環形分布動載荷識別方法。由于B樣條函數的分段、高階導數連續等特性，識別出的分布動載荷能同時保證識別效率與精度。最后，將本文提出的識別方法應用于衛星結構星箭界面動載荷識別。

1 動載荷識別原理

1.1 基于脈沖響應函數的動載荷識別

在時域內，若用脈沖信號作為單元信號，可將動態載荷表示為一系列脈沖函數的疊加。當線性系統在連續時間域內只受到單源載荷時，系統的響應在時域內可以表示成如下激勵與脈沖響應函數的卷積分的形式：

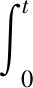
(1)

式中：y(t)為結構上測點處的響應，q(τ)是載荷的時間歷程，g(t-τ)為載荷作用點到結構上響應測點的單位脈沖響應。

將式(1)中的卷積分在時間域內用m個等間隔的采樣點進行離散，可轉化為一組線性方程組：

(2)

式中：yi，gi，qi分別為t=iΔt時刻結構的響應、脈沖響應函數和待識別的載荷；Δt為離散的采樣時間間隔；m為采樣點的數目。將式(2)表示為如下矩陣形式：

Y=GQ

(3)

式中：Y為結構響應yi組成的列矩陣，G為脈沖響應函數gi組成的脈沖響應函數矩陣，Q為待識別載荷qiΔt組成的列矩陣。

對于多源載荷，類似于單源載荷作用下的推導過程，依據疊加原理，可將多源載荷問題表示為如下矩陣形式：

(4)

式中：m表示響應測點個數，n表示待識別載荷的個數；Yi為第i個測點的響應組成的列矩陣；Qj為第j個待識別載荷在采樣點處的值qj,kΔt組成的列矩陣；Gi,j為第j個待識別載荷作用點到第i個測點的脈沖響應矩陣。

1.2 B樣條基函數

在區間[x0,xn)上，k次B樣條基函數的遞推定義如下：

(5)

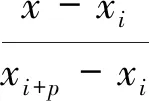
(6)

式(5)～(6)通常稱為Cox-de Boor遞歸公式，其中，p為B樣條基函數的次數；Ni,p(x)是第i個p次的B樣條基函數；xi為節點。

由于三次B樣條函數具有二階導數連續的性質，因此本文的研究中選用三次B樣條基函數，其形式如圖1所示，則B樣條函數可擬合為：

(7)

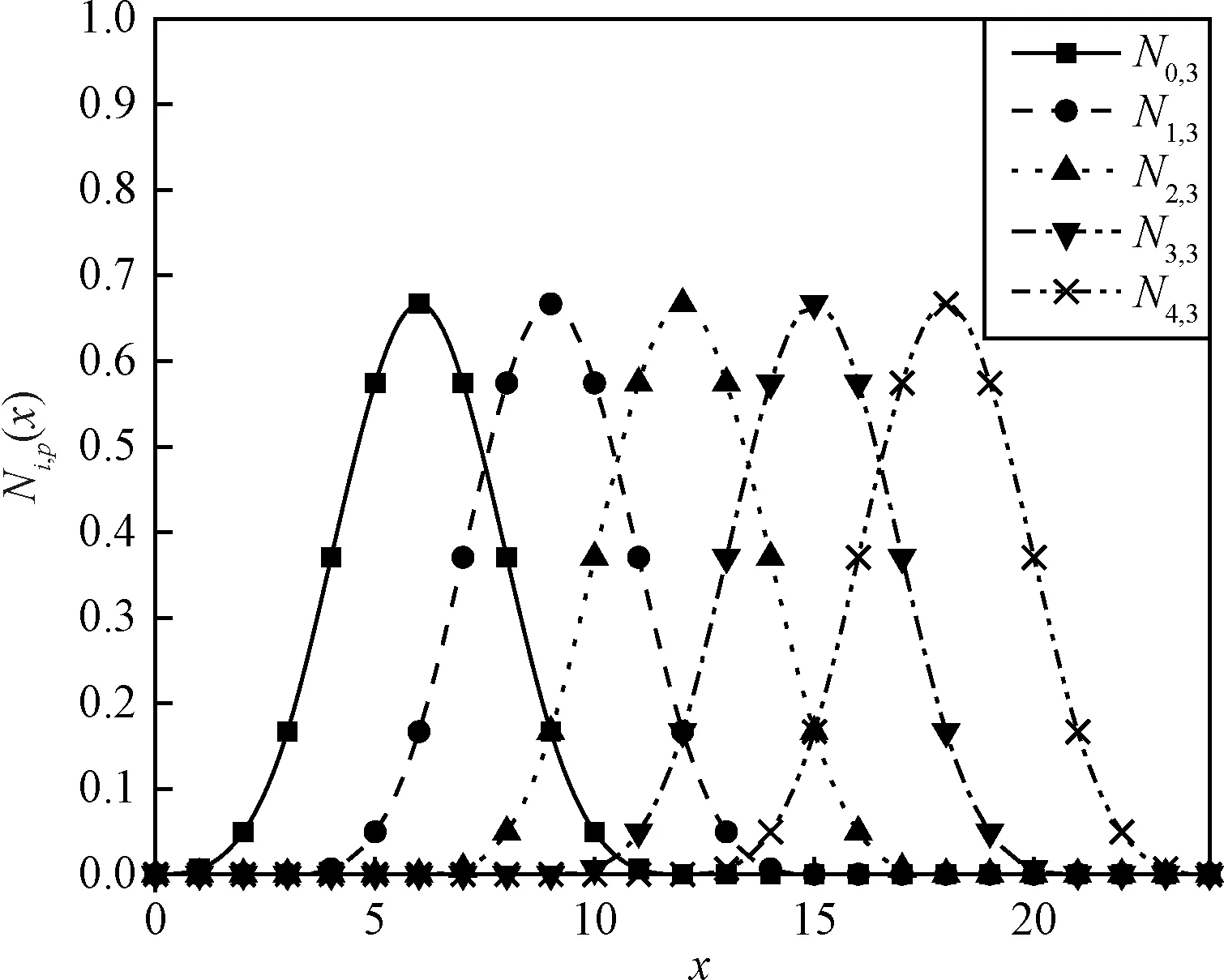
圖1 三次B樣條基函數Fig.1 Basis function of cubic B-spline

1.3 環形分布動載荷識別

對于環形分布載荷，考慮周期性邊界條件，其空間分布可通過B樣條基函數表示為：

(8)

式中：B(x)為環形分布式動載荷的空間分布，Ni,p(x)為第i個p次B樣條基函數，Bi為第i個p次B樣條基函數的系數，N為基函數個數。

作用在結構上的環形分布式動載荷q(x,t)可以表示為：

q(x,t)=B(x)s(t)

(9)

式中：s(t)表示隨時間變化的動載荷。

將式(8)代入式(9)，可將環形分布式動載荷q(x,t)表示為：

(10)

結合有限元模型，針對圖2中的環形分布動載荷，將動載荷的分布函數沿環劃分為N段，設置N個控制節點，將兩個控制點之間的部分繼續劃分為多個單元，有限元節點總數為n個。如圖2所示，將動載荷分布函數沿環形劃分為8段，則N=8。在確定B樣條基函數次數及控制點個數之后，基函數形式亦隨之確定。假設共選取m個測點獲取響應信息。

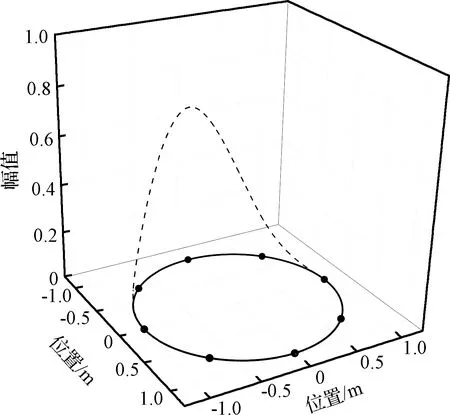
圖2 B樣條基函數形式的脈沖激勵Fig.2 The B-spline basis impulse excitation

利用有限元方法，通過形函數積分可將分布式動載荷q(x,t)轉化為結構的單元節點載荷Fe(t)：

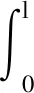
(11)

式中：Ne(x)為單元形函數。

將式(10)代入式(11)，節點載荷可表示為：

(12)

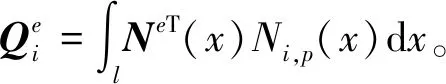
則節點載荷向量可表示為：

(13)

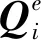
依據第1.1節的動載荷識別理論，在多源載荷作用下，結構測點響應可表示為：

(14)

式中：fj(τ)為第j個節點載荷的時間歷程，gk,j(t-τ)為從第j個激勵節點到第k個響應測點的脈沖響應函數，n為動載荷環形分布的有限元節點數。

將式(13)代入式(14)可得：

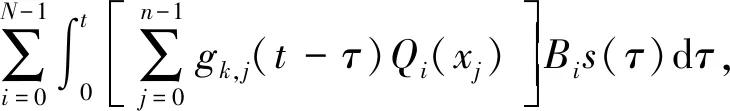
k=1,2,…,m

(15)

式中：Qi(xj)為第i個B樣條基函數形式的分布載荷經有限元方法轉化后的第j個節點上的載荷。

記

(16)

則式(15)可轉化為

(17)

式中：Gk,i(t-τ)為在結構上作用第i個B樣條基函數分布形式的脈沖激勵后(見圖2)測點k處所得到的脈沖響應函數。

式(17)可表示為如下矩陣形式：

(18)

式中：yk，si分別表示第k個測點處響應yk和第i個控制點處激勵si在各時間點的值所組成的列矩陣；Gk,i是結構在第i個p次B樣條基函數Ni,p形式的脈沖激勵作用下，第k個測點處得到的脈沖響應函數所組成的脈沖響應矩陣。

式(18)可簡化為：

Y=GBs

(19)

式中：Y為m個測點的加速度響應yk組成的列矩陣，G為脈沖響應矩陣組裝成的傳遞矩陣，Bs為樣條基函數系數Bi與激勵在各時間點的值si的乘積組成的列矩陣。

利用最小二乘法，得到實測加速度響應與基礎加速度激勵的關系為：

Bs=(GTG)-1GTY

(20)

在動載荷識別過程中，矩陣G的病態可能引起式(20)求解結果的較大誤差，可利用正則化方法來提高求解精度。

基于B樣條函數的分布動載荷識別步驟為：

(1)確定B樣條基函數次數p(階數p+1)及環形分布動載荷作用處的分段數(控制點數)，由遞歸公式(5)～(6)確定B樣條基函數的函數形式Ni,p。

(2)在結構上分別施加各段B樣條基函數形式的脈沖激勵，得到測點的脈沖響應函數，組裝獲得式(19)中的傳遞矩陣G。

(3)根據式(20)，由測點加速度響應y反演B樣條基函數系數Bi與基礎激勵時程s(t)的乘積。

(4)由式(10)重構獲得環形分布動載荷q(x,t)。

2 算例研究

為校驗本文提出的方法，針對尺寸和材料參數如表1所示的某衛星結構，建立如圖3所示有限元模型，開展數值仿真研究。衛星底座處受到環形分布動載荷激勵，其有限元網格以及節點及控制點編號情況如圖4所示。

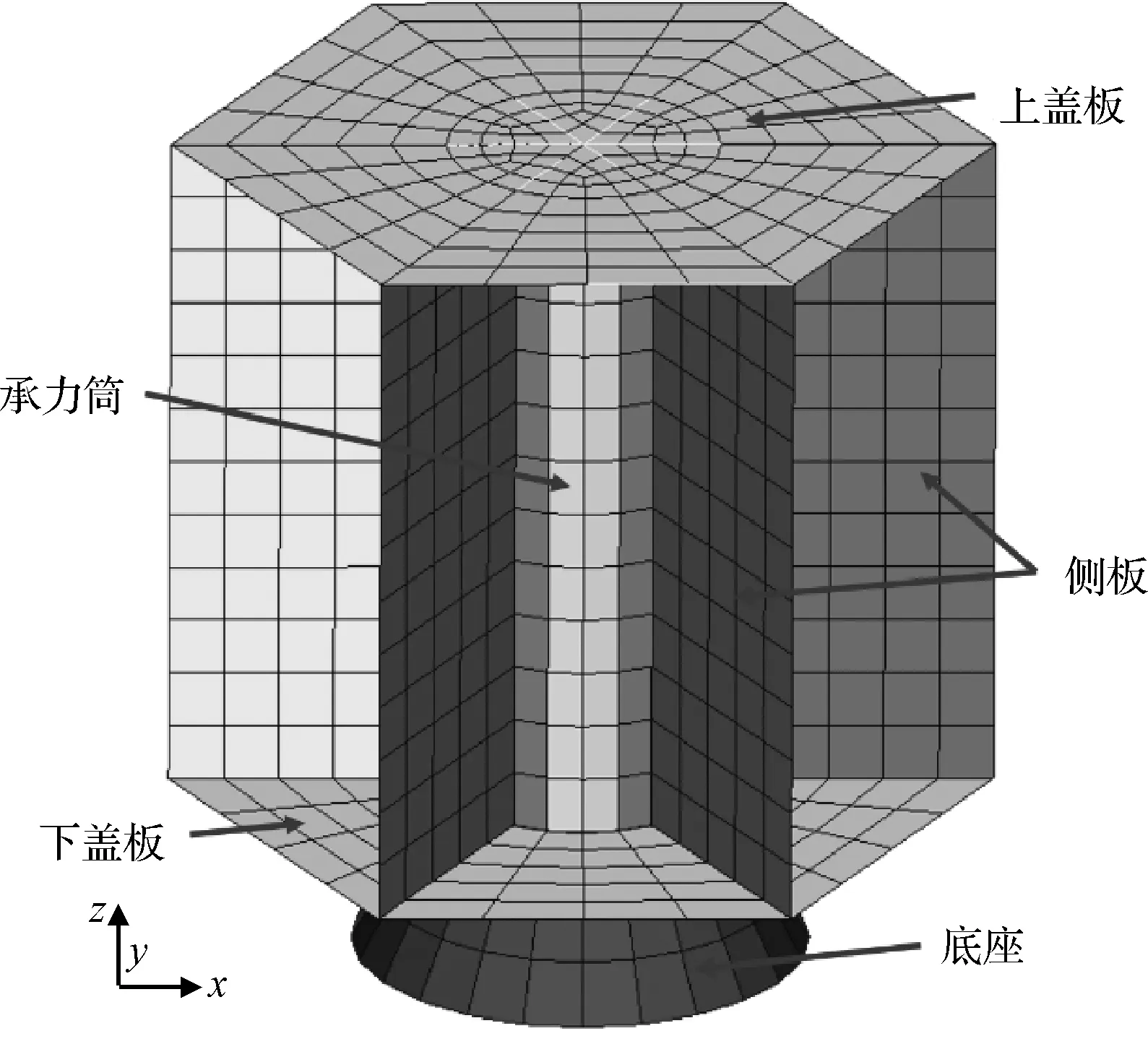
圖3 衛星有限元模型Fig.3 Finite element model of satellite

表1 衛星模型尺寸及材料參數Table 1 Dimension and material parameters of satellite model

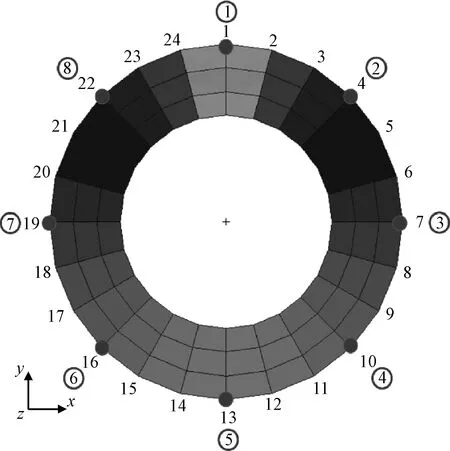
圖4 節點與控制點排布及編號Fig.4 Arrangement and number of nodes and control points

衛星有限元模型所在坐標系如圖3所示，在底部施加約束，僅釋放z方向的平動自由度。衛星結構上的響應測點選取對動載荷識別結果有重要影響，因此需要通過頻響分析，選擇對底部加速度激勵敏感的測點。在底部施加單位頻域加速度激勵，頻率范圍為0～100 Hz，能夠覆蓋模型前10階固有頻率，獲得衛星結構的加速度頻率響應云圖(見圖5)，圖5中給出了衛星模型一階頻率附近4 Hz處的頻率響應云圖。在頻率響應云圖數值較大處，如上、下蓋板以及承力筒上布置測點，測點編號及位置如圖5所示。

動載荷識別仿真研究中，需要測點的加速度響應作為輸入數據。加速度響應的計算方法如下：在衛星底部作用一沿環形分布的基礎加速度激勵q(x,t)，其中B(x)為基礎加速度激勵的空間分布函數，有

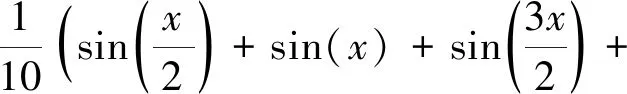
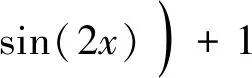
(21)

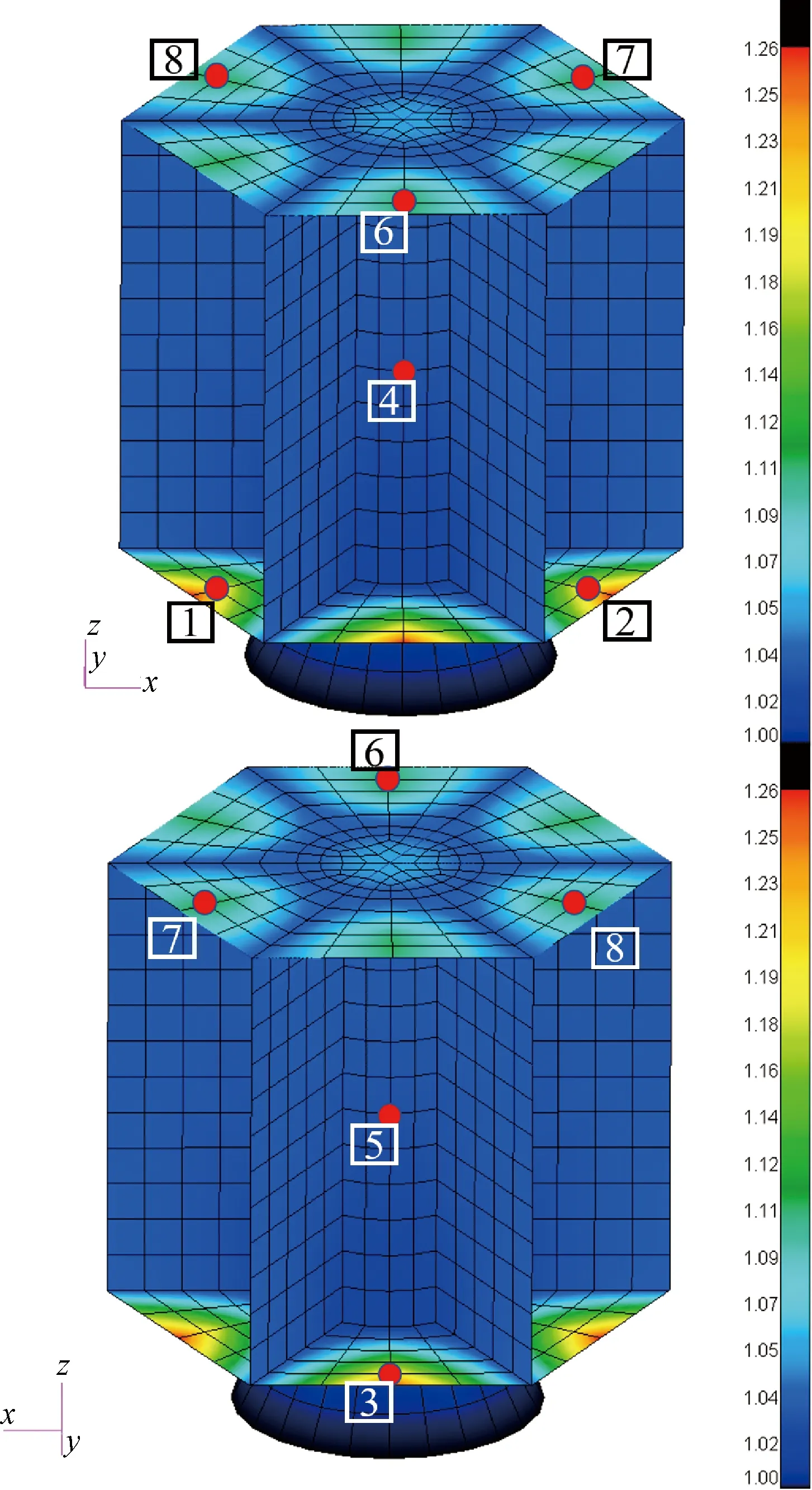
圖5 4 Hz處(模型一階固有頻率)頻率響應云圖Fig.5 Cloud chart of frequency response at 4 Hz (first order natural frequency of model)

s(t)為分布動載荷的時變分量，在本節算例中，依據高斯隨機過程的功率譜獲得s(t)的時程曲線：

(22)

式中：Δω表示頻率增量；ωk=ωmin+Δω(k-1)；Nk表示區間[ωmin,ωmax]上頻率劃分的總個數，Nk=(ωmax-ωmin)/Δω；ψk表示均勻分布于區間[0,2π]內的隨機相位角；Φ(ω)表示零均值非平穩高斯隨機過程的雙邊功率譜密度函數，有如下定義：Φ(ω)=(1/2π)(2/ω2+1)，具體參數設置如表2所示。

衛星結構加速度響應分析時長為0.5 s，步長為0.0005 s，施加于圖3中有限元模型底部z方向，得到結構上各測點處的加速度響應。利用仿真得到的各測點處的加速度響應，根據第1.3節中的動載荷識別步驟，開展衛星結構底部環形分布加速度激勵的識別。在求解式(20)時，采用Tikhonov正則化方法提高列矩陣Bs求解精度，采用廣義交叉驗證準則確定最優正則化參數。

表2 s(t)時程曲線的參數設置Table 2 Parameter settings for the time history of s(t)

為了定量給出基礎加速度激勵時程的識別精度，引入對數相對誤差計算公式：

(23)

式中：Ai,C為識別加速度激勵的第i個峰值，Ai,E為參考加速度激勵的第i個峰值；n為峰值個數。

為了定量給出基礎加速度激勵空間分布的識別精度，引入相對誤差計算公式：

(24)

2.1 無測量噪聲情況下的識別結果

將動載荷分布函數沿環劃分為8段，設置8個控制節點，控制點位置及有限元節點編號如圖4所示，確定B樣條基函數形式；在結構上選取8個測點，由測點處加速度響應反演得到衛星底座處各節點的基礎加速度激勵時程曲線及激勵的空間分布。某節點處基礎加速度激勵識別結果如圖6～7所示，識別誤差如表3所示。

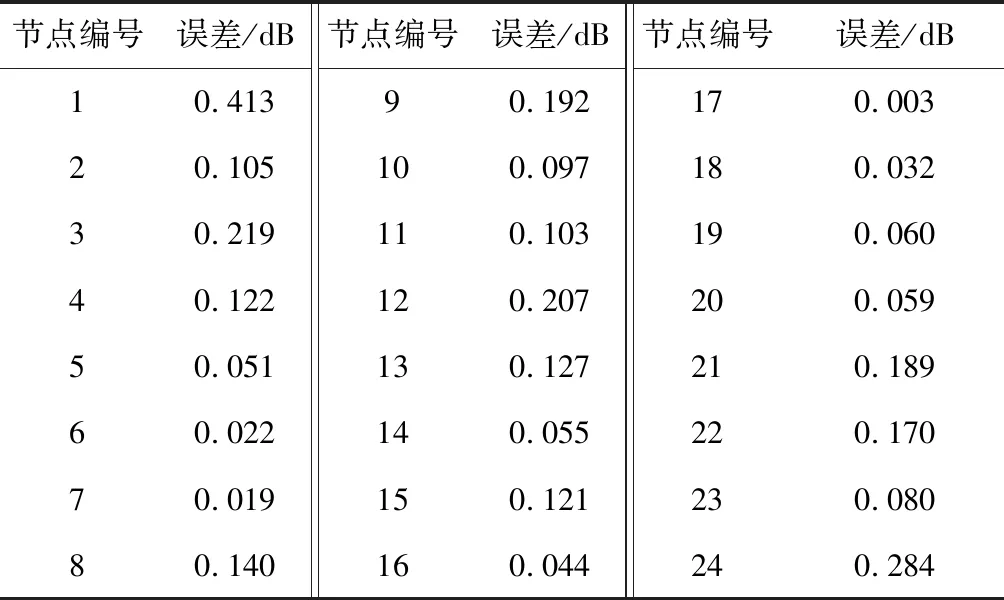
表3 各節點基礎加速度激勵識別誤差Table 3 Identification error of base acceleration excitation at each node

從圖6～7和表3可以看出，在無噪聲情況下，各節點處基礎加速度激勵識別結果非常準確，平均峰值誤差為0.122 dB；基礎加速度激勵的空間分布識別的誤差為5.37%，誤差較小，表明本文提出的環形分布動載荷識別方法具有可行性。

2.2 測量噪聲對識別結果的影響

在控制點數及測點數均與第2.1節相同的情況下，在衛星結構加速度響應中分別加入10%和15%的噪聲，開展測量噪聲對動載荷識別結果的影響研究。噪聲施加方式為：

Yerr=Ycal+lnoisestd(Ycal)rand(-1,1)

(25)

式中:Ycal是計算得到的位移響應；std(Ycal)是計算的位移響應的標準差；lnoise是個百分數，代表噪聲水平；rand(-1,1)是[-1,1]之間的隨機數。

由測點加速度響應反演得到衛星底座處各節點的基礎加速度激勵時程曲線。圖8、圖9分別給出了在不同噪聲水平下基礎加速度激勵時程識別值與參考值對比，識別誤差如表4所示。

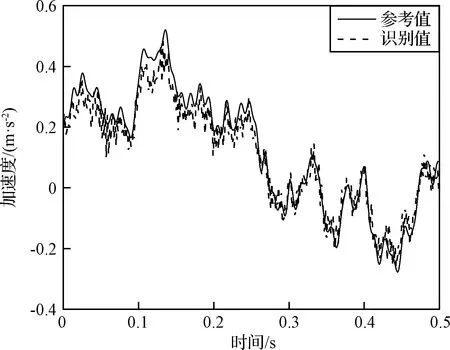
圖8 節點4處加速度識別值參考值對比(10%噪聲水平)Fig.8 Comparison of identified and referenced base acceleration excitation at node 4(10% noise level)

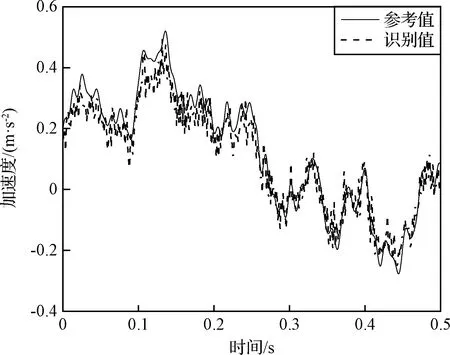
圖9 節點4處加速度識別值參考值對比(15%噪聲水平)Fig.9 Comparison of identified and referenced acceleration excitation at node 4(15% noise level)

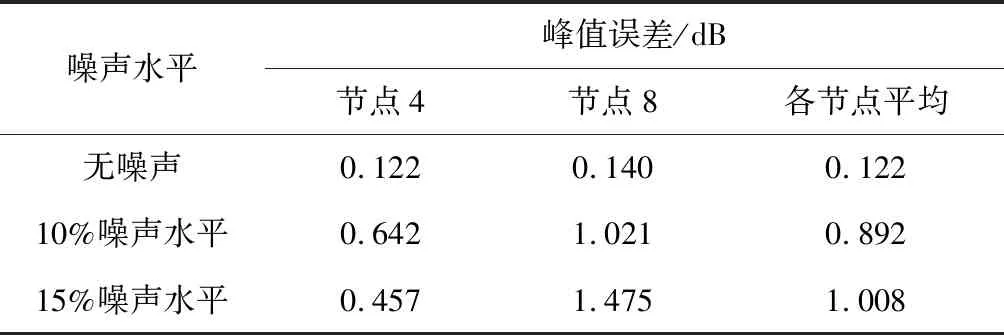
表4 不同噪聲水平下基礎加速度激勵識別誤差Table 4 Identification error of base acceleration excitation under different noise levels

從圖6、圖8～9和表4可以看出，隨著噪聲水平的提高，載荷識別的精度有所下降，但在噪聲水平比較高的情況下，基礎加速度激勵的時間歷程依然能被比較準確地重構出來，節點平均峰值誤差小于1.5 dB，說明本文所述的計算方法能抑制噪聲對載荷識別結果的影響，具有較好地穩定性。

2.3 測點數對識別結果的影響

在控制點數與第2.1節相同的情況下，依據圖5中由頻響函數值選擇測點的方法，在結構上分別選取不同的測點數目，在10%噪聲水平下，由測點加速度響應反演得到衛星底座處各節點的基礎加速度激勵時程曲線及空間分布。圖10～13給出了不同測點數下基礎加速度激勵時程及空間分布的識別值與參考值對比，識別誤差如表5所示。

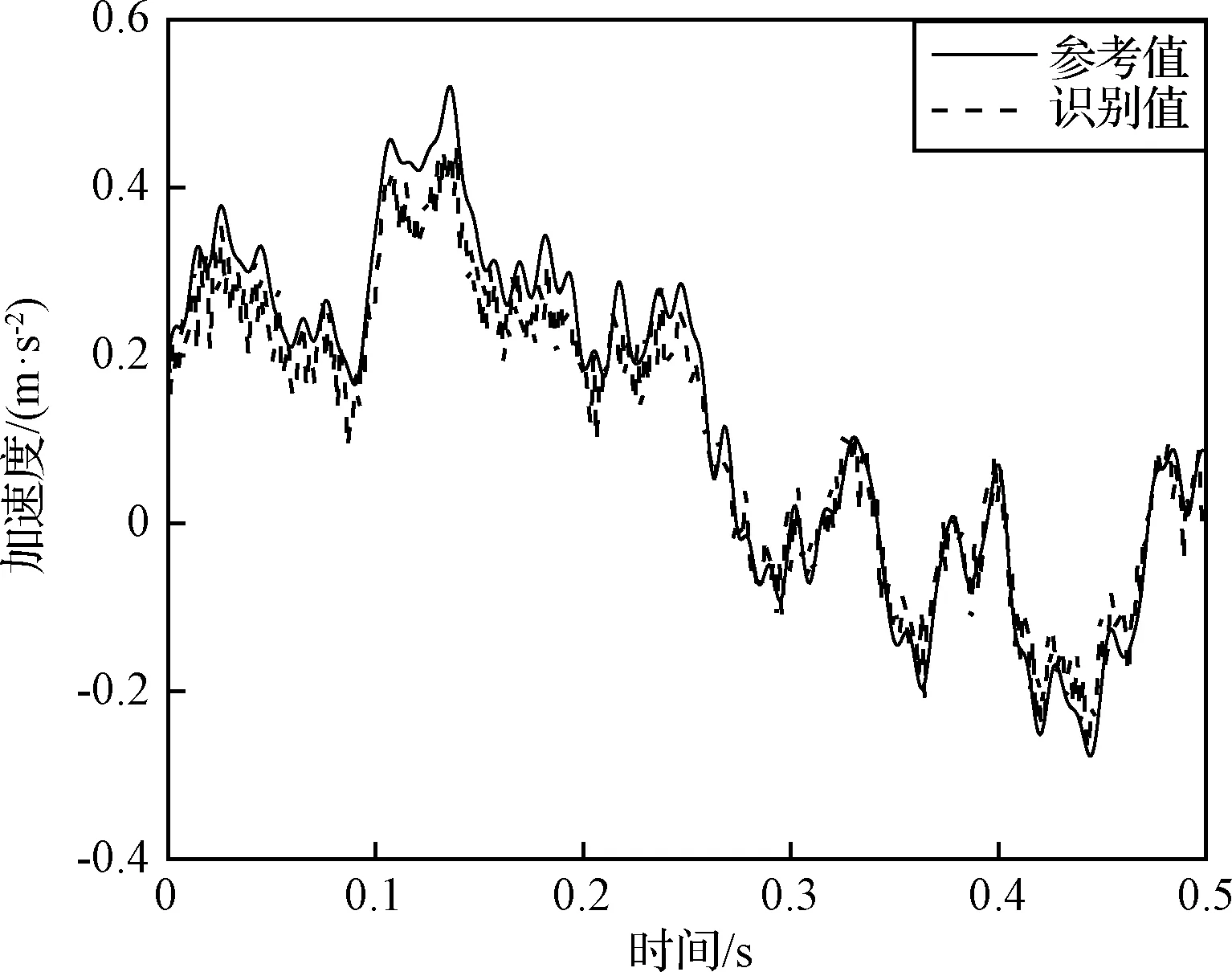
圖10 節點4處加速度識別值與參考值對比(12測點)Fig.10 Comparison of identified and referenced acceleration excitation at node 4(12 measurement points)

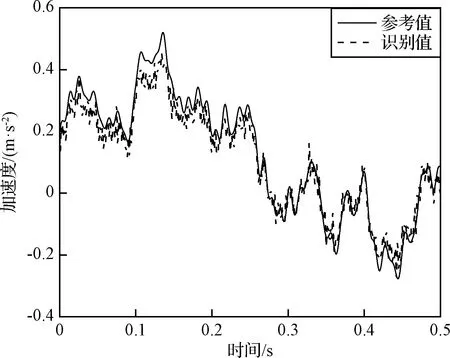
圖11 節點4處加速度識別值與參考值對比(16測點)Fig.11 Comparison of identified and referenced acceleration excitation at node 4(16 measurement points)

從圖8、圖10～13和表5可以看出，在控制點數一定的情況下，當滿足測點個數大于或等于待識別B樣條基函數系數個數的條件時，三種工況下動載荷時間歷程識別的平均峰值誤差小于1 dB，動載荷空間分布識別的誤差小于6%，均能較為準確地重構出環形分布動載荷的時間歷程與空間分布，表明本文方法可以在使用少量測點的條件下保證動載荷識別的精度。

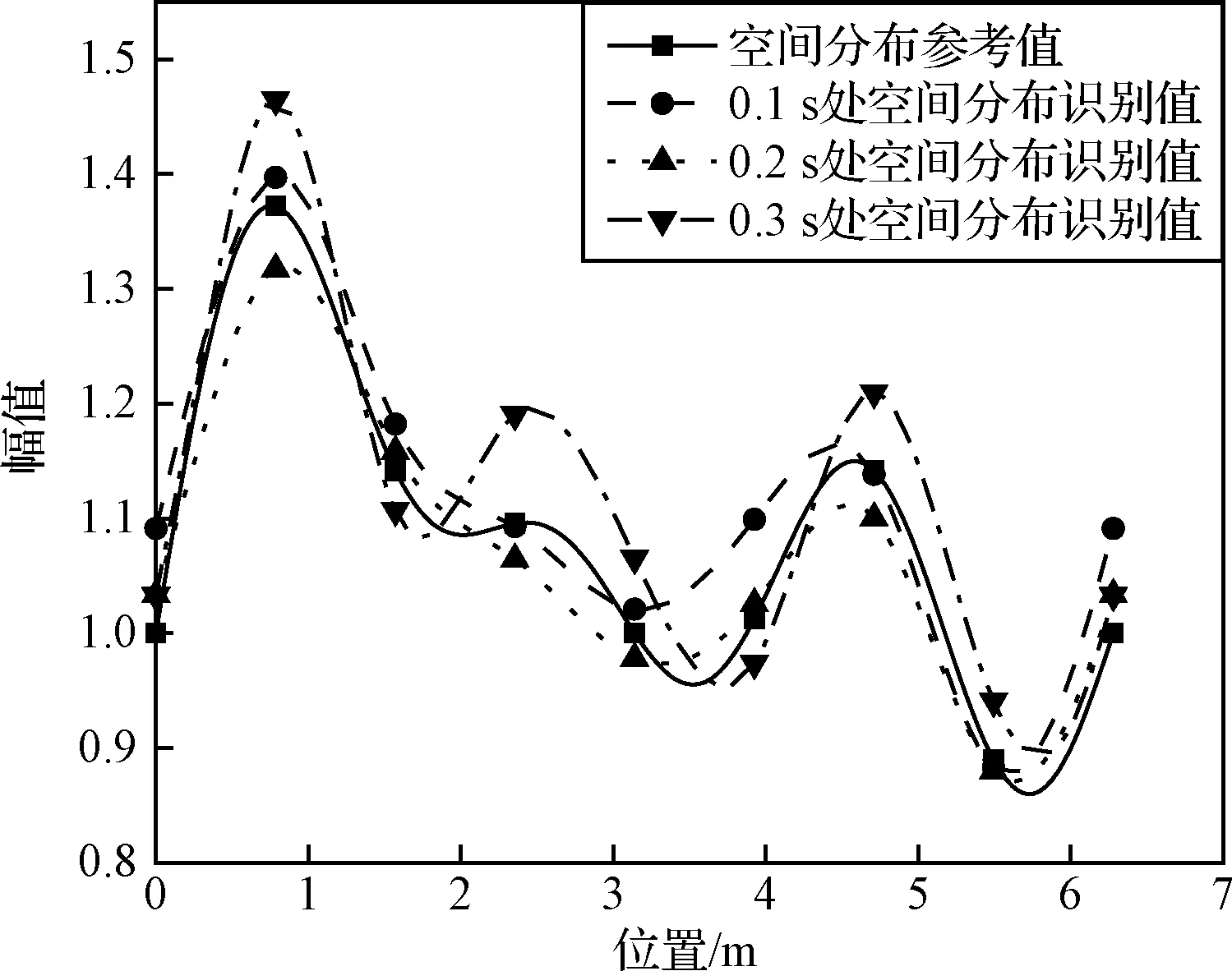
圖12 加速度激勵空間分布識別值參考值對比(12測點)Fig.12 Comparison of identified and referenced spatial distribution of acceleration excitation(12 measurement points)

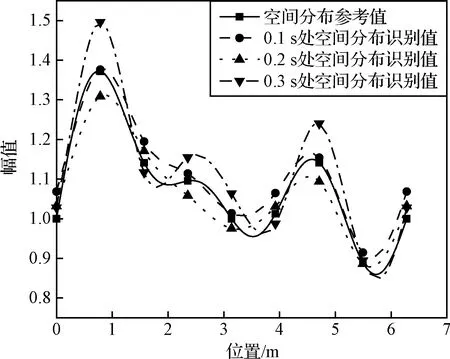
圖13 加速度激勵空間分布識別值參考值對比(16測點)Fig.13 Comparison of identified and referenced spatial distribution of acceleration excitation(16 measurement points)

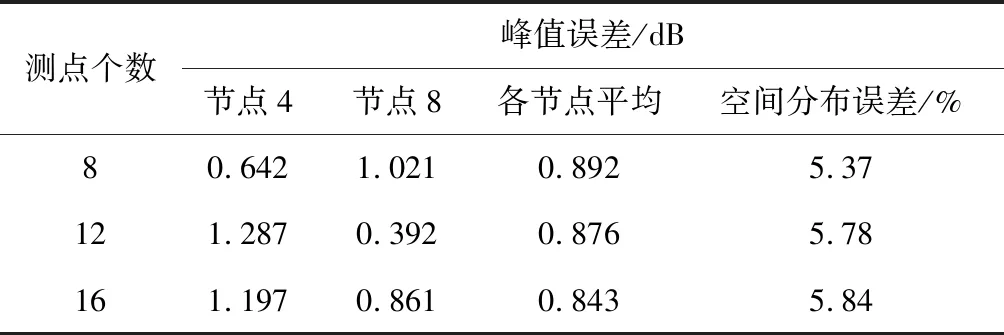
表5 不同測點數下基礎加速度激勵識別誤差Table 5 Identification error of base acceleration excitation of different number of measurement points

2.4 控制點數對識別結果的影響

根據圖4等分動載荷分布函數的方法，分別在衛星底部選擇不同的控制點數目，分別確定B樣條基函數表達式，在10%噪聲水平下，由測點加速度響應反演得到衛星底座處各節點的基礎加速度激勵時程曲線及空間分布。圖14～17分別給出了在不同控制點數下基礎加速度激勵時程及空間分布的識別值與參考值對比，識別誤差如表6所示。

從圖8、圖14～17和表6可以看出，在本算例中，如選擇6個控制點，動載荷的空間分布識別誤差超過了10%；當控制點數增加至8以上時，動載荷識別的精度顯著提高，空間分布的識別誤差低于6%，節點的平均峰值誤差小于1 dB，表明控制點數的增加可以有效提高環形分布動載荷的時間歷程與空間分布的識別精度。

圖14 節點4處加速度識別值參考值對比(6控制點)Fig.14 Comparison of identified and referenced acceleration excitation at node 4(6 control points)

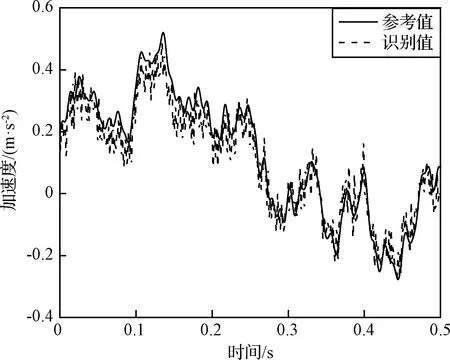
圖15 節點4處加速度識別值參考值對比(12控制點)Fig.15 Comparison of identified and referenced acceleration excitation at node 4(12 control points)

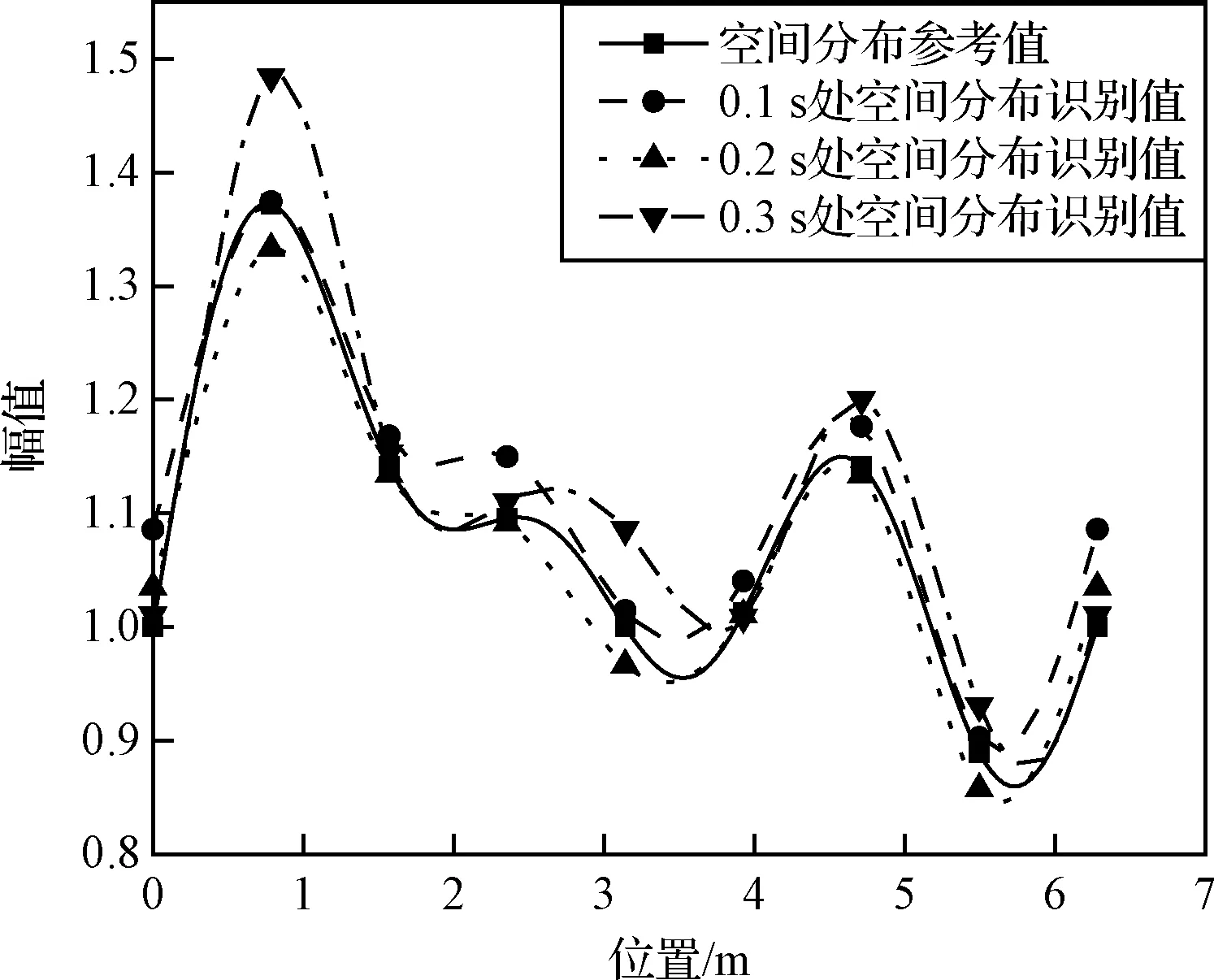
圖16 加速度激勵空間分布識別值參考值對比(8控制點)Fig.16 Comparison of identified and referenced spatial distribution of acceleration excitation(8 control points)

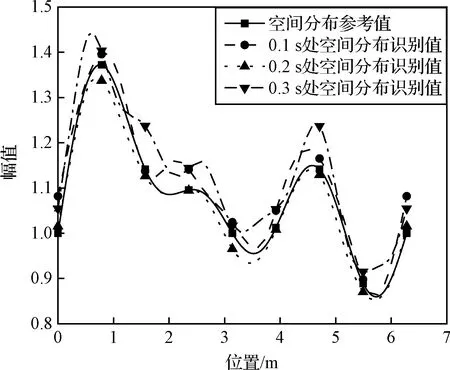
圖17 加速度激勵空間分布識別值參考值對比(12控制點)Fig.17 Comparison of identified and referenced spatial distribution of acceleration excitation(12 control points)

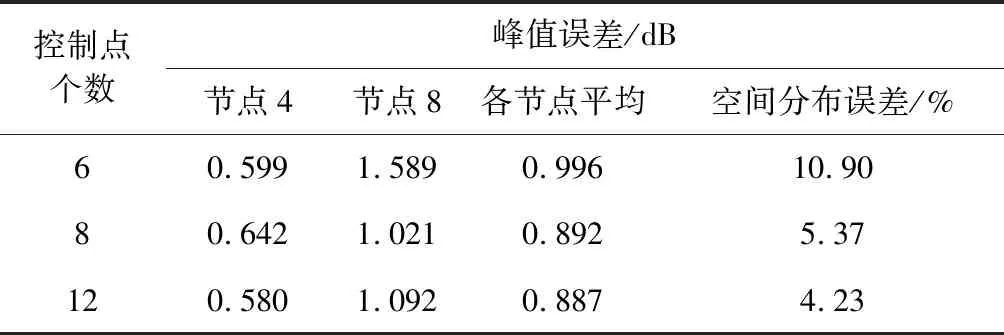
表6 不同控制點數下基礎加速度激勵識別誤差Table 6 Identification error of base acceleration excitation of different number of control points

3 結 論

本文用B樣條函數表示動載荷分布函數，提出一種環形分布動載荷的識別方法，并將該方法應用于衛星結構底座處星箭連接界面的動載荷識別。對識別方法開展數值仿真研究，校驗了該識別方法的有效性，討論不同測量噪聲水平，測點數，B樣條控制點數等因素對動載荷時程以及空間分布識別結果的影響，結果表明：

1)噪聲對動載荷識別精度有一定的影響，由于B樣條本身具有平滑特性，本文的動載荷識別方法對響應中的測量噪聲具有較好的魯棒性。

2)在控制點數與噪聲水平一定的情況下，當滿足測點個數不小于待識別B樣條基函數系數個數的條件時，較少的測點數目即可保證動載荷識別結果的精度。

3)在噪聲水平一定的情況下，增加控制點數，可以有效提高動載荷的識別精度，特別是動載荷分布函數識別結果的精度。

對于具有周期性特征的環形分布動載荷，本文提出的方法能保證識別出的動載荷空間分布的首尾連續性，也能保證動載荷空間分布函數導數的連續性；相比傳統的識別方法，能減少測點數，降低矩陣的維數，減小反問題計算過程中矩陣的病態性，識別效率和精度較高。本文方法中，關于B樣條基函數次數及控制點數量的確定準則，還值得進一步研究。