譜估計理論在彈道數據參數化建模中的應用

張 召，荊武興，李君龍，高長生

(1. 哈爾濱工業大學航天學院，哈爾濱 150001；2. 中國航天科工集團有限公司第二研究院，北京 100854)

0 引 言

憑借高速度和高機動性能，高超聲速飛行器具備極強的突防能力，對現代防御體系構成了巨大威脅。為對其進行有效的跟蹤、預報和攔截，需要對其彈道特性進行深入研究，了解其運動規律并進行參數化建模。

目前針對彈道特性的研究，大都基于飛行器的動力學模型，采用基于標稱彈道的線性化[1-2]、分岔理論[3-4]和多尺度理論[5-6]等方法，研究制導參數對彈道數據的影響規律。然而，對于防御方來說，進攻方飛行器的制導規律和動力學模型是不可觀測的，而且在線識別的技術難度較大[7]。因此，本文將飛行過程視作黑箱模型，針對可觀測的彈道數據開展研究，分析其變化規律并給出參數化描述。相較于傳統研究方法，本文方法著重于挖掘彈道數據自身的內在規律，可以為不同飛行器提供統一的彈道描述方式，而且易于利用跟蹤數據進行在線建模，為實現彈道層面的匹配、識別和預報奠定基礎[8-9]。

針對數據內在規律的挖掘，時間序列分析以及信號處理等領域都有豐富的研究成果。信號處理領域的譜估計理論，可以在輸入未知的情況下，對平穩輸出序列進行分析和建模。尤其是功率譜估計，是經常被采用的一種重要方法，反映了信號功率隨頻率的分布。具體可分為經典譜估計和現代譜估計[10]，其中現代譜估計的參數模型法可以給出信號的參數化描述。以參數模型法描述目標運動已有諸多研究，文獻[11-13]使用自回歸(Auto-regressive，AR)模型描述人和機器人的運動規律并進行預報；文獻[14-16]采用AR模型提取彈道目標的進動特性；文獻[17-18]則在模型中引入了輸入量，研究競技體育中目標的軌跡特性。數據平穩是應用譜估計理論的前提，但是高超聲速飛行彈道數據帶有明顯的趨勢，不符合該前提。本文采用線性消勢法消除彈道數據的線性趨勢，將其轉變為平穩信號，進而采用譜估計理論進行分析和建模。

應用參數模型的過程中，最重要的步驟之一就是模型階數的選擇。作為一般規律，如果模型階數選擇太低，將會得到一個高度平滑譜；如果選擇得太高，則可能在譜中引入虛假低峰[10]。為此，相關學者提出了不同的選擇準則：F-檢驗、最終預報誤差(Final prediction error，FPE)準則、Akaike信息準則(Akaike information criterion，AIC)、貝葉斯信息準則(Bayesian information criterion，BIC)等。然而，一些試驗結果表明，模型階數選擇準則不能生成確定的結果[10]。為克服該問題，本文將經典譜估計引入模型階數的選擇過程。以經典譜估計生成的彈道數據譜圖為參考，對參數模型階數進行調整，以完成模型階數的確定。

本文以高超聲速飛行彈道為對象，研究參數化建模方法。以典型彈道數據為基礎，使用線性消勢法將其轉變為平穩信號；綜合使用經典譜估計中的Welch直接法和現代譜估計中的AR參數模型法，對彈道數據進行參數化分析和建模。文章最后以彈道地心距為例進行了仿真校驗，驗證了本文算法所確定模型與動力學模型的一致性。

1 高超聲速飛行彈道

進行彈道數據譜估計的基礎是充足的數據支持，既可以是先驗的彈道數據，也可以是實時的跟蹤數據。本節以動力學模型和典型飛行模式為基礎，通過數值仿真方法獲得典型高超聲速飛行器的先驗彈道，為后文分析其變化規律并實現參數化建模提供數據支持。高超聲速飛行在彈道系下表示為[19]：

(1)

(2)

(3)

(4)

(5)

(6)

典型的飛行模式包括常攻角飛行、常升阻比飛行、最大升阻比飛行、平衡滑翔飛行以及指標最優飛行[20]。其中指標最優包括：射程最優、末速最大、氣動加熱最少以及突防性能最優等[21-24]。

2 基于Welch算法的彈道數據分析

將彈道數據視作信號，使用信號處理領域的譜估計理論對其進行研究。在實際工作中，往往假定信號是平穩的和各態遍歷的[10]。然而，高超聲速飛行彈道除了小范圍的波動外，具有明顯的趨勢，直接進行譜估計會導致較大的偏差。本節采用線性消勢法提前消除信號的趨勢，將其轉變為平穩信號，再使用經典譜估計理論生成信號的譜圖。

2.1 消除信號趨勢

消除信號趨勢的主要方法有線性消勢和差分消勢。考慮到差分消勢會引入運動的高階信息而且高超聲速飛行彈道具有波動特性，采用差分消勢會導致較高的模型階數，增大計算量甚至引入虛假低峰。本文采用線性消勢法，將數據信號的趨勢表述為線性形式：

d(n)=a+bn

(7)

結合生成的彈道數據，以擬合方式確定式(7)系數；然后從原始信號中消除相應的線性部分，即可完成消勢。消除趨勢后的數據信號可視作平穩的和各態遍歷的，可以開展進一步的研究。

2.2 Welch算法

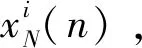
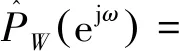
(8)

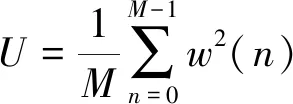
Welch算法很好地改善了周期圖法譜估計的方差特性，而且概念清晰、方法簡便。本文采用Welch算法對彈道數據進行初步分析，給出大致的功率譜特性，為后文進行更加精確的譜估計和參數化建模提供參考。

3 基于AR模型的彈道數據參數化建模

經典譜估計可以給出大致準確的譜圖，但是無法給出數據的參數化描述，不利于開展進一步的研究。現代譜估計的AR參數模型法不僅可以提高功率譜估計的分辨率，而且可以建立數據的參數化模型。然而，仍存在模型階數選擇準則引起的不確定性問題。本節采用AR模型描述彈道數據的內在規律，以改進的協方差法為基礎對其進行求解，并結合AIC、AR模型譜圖和Welch算法譜圖確定具體的模型階數。

3.1 平穩信號的AR模型

假定所研究信號x(n)是由一個輸入信號u(n)激勵一個線性系統H(z)的輸出，則x(n)和u(n)之間有如下關系：

(9)

式中：若x(n)是確定性的，那么u(n)是一個沖激序列；若x(n)是隨機的，那么u(n)是一個白噪聲序列。

如果b1,b2,…,bq全為0，則有：

(10)

在Z域上，轉移函數為：

(11)

可見，上述模型僅有極點，這種全極點模型即為AR模型。其含義是，模型當前輸出由當前輸入和過去p個時刻的輸出決定。

本文中輸入序列是不可觀測的，但是如果輸出序列表現為平穩隨機過程，那么輸入序列也被假定為平穩隨機過程[10]。因此，假定u(n)是一個白噪聲序列，方差為σ2；由隨機信號通過線性系統的理論可知，x(n)的功率譜為：

(12)

確定式(12)中的白噪聲方差σ2及模型的系數a1,a2,…,ap，即可求出x(n)的功率譜。

3.2 AR模型系數確定

目前提出的有關AR模型系數的求解及AR模型性能的討論大都是建立在線性預測理論上的，而且這些算法的性能一般要優于自相關法[10]。而且AR模型和線性預測器是等價的，AR模型的白噪聲能量σ2等于線性預測器的最小預測誤差功率ρmin。不失一般性，令前后預測誤差功率之和：

(13)

為最小。上標f表示前向預測，上標b表示后向預測。式(13)中：

(14)

(15)

在令ρfb為最小時，不是僅令ρfb相對am(m)=km為最小，而是令ρfb相對am(1),am(2),…,am(m)都為最小，m=1,…,p。

由ab(k)=af*(k)，令

(16)

(17)

即

(18)

又令

(19)

寫成矩陣形式：

(20)

最小預測誤差功率可由式(21)～(22)求出：

(21)

或者

(22)

式(22)即為改進的協方差方法的正則方程，許多學者給出了相應的求解算法[10]。

3.3 AR模型階數選擇

為解決上述問題，本文將經典譜估計引入AR模型階數的選擇過程：首先，模型階數由1逐步增加，計算AIC：

(23)

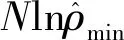
本節所設計的模型階數選擇算法，綜合考慮了時域指標和頻域指標，分別從時域和頻域兩個角度分析所建模型的精度。其中，時域指標由改進的協方差方法求解得到，描述了模型誤差的統計特性；頻域指標由Welch算法的估計結果提供參考，用以評估AR模型譜圖的質量。兩個指標的綜合運用，可以有效改善僅有時域指標造成的不確定性問題，提高建模精度和可靠性。

4 仿真校驗

以HTV-2最大升阻比飛行彈道的地心距為例進行仿真分析，初始高度45 km，速度6 km/s，當地速度傾角0°，飛行時長1178 s，采樣周期0.1 s，地心距如圖1所示。可見地心距呈現波動下降，并且振蕩幅值逐步衰減。下面將地心距數據視作信號，分析其功率譜并建立參數化模型，最后對所建立的模型進行驗證。

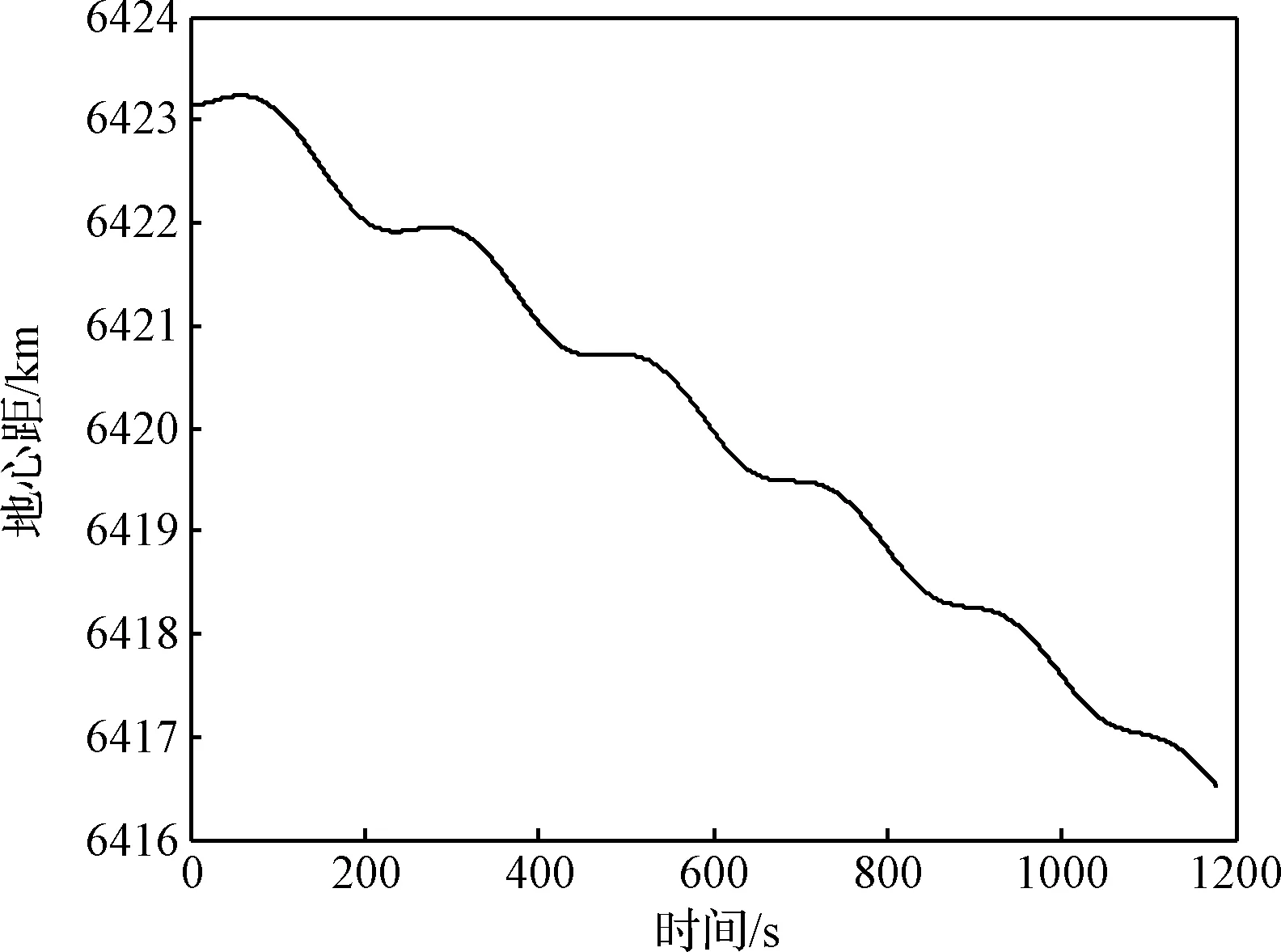
圖1 地心距信號時域圖Fig.1 Time domain diagram of geocentric distance signal

使用Welch算法分析地心距信號的功率譜，如圖2所示。可見在0.02667 rad/s處存在一個轉折頻率，而且在低頻部分存在更大的能量。對照地心距信號時域圖可知，地心距為非平穩信號，呈現波動減小趨勢：小范圍波動即為轉折頻率所代表的部分，減小趨勢即是低頻部分。該非平穩信號具有較大的頻域跨度，不利于對信號進行精確分析和建模，需要消除信號的趨勢，也就是消除其低頻部分。

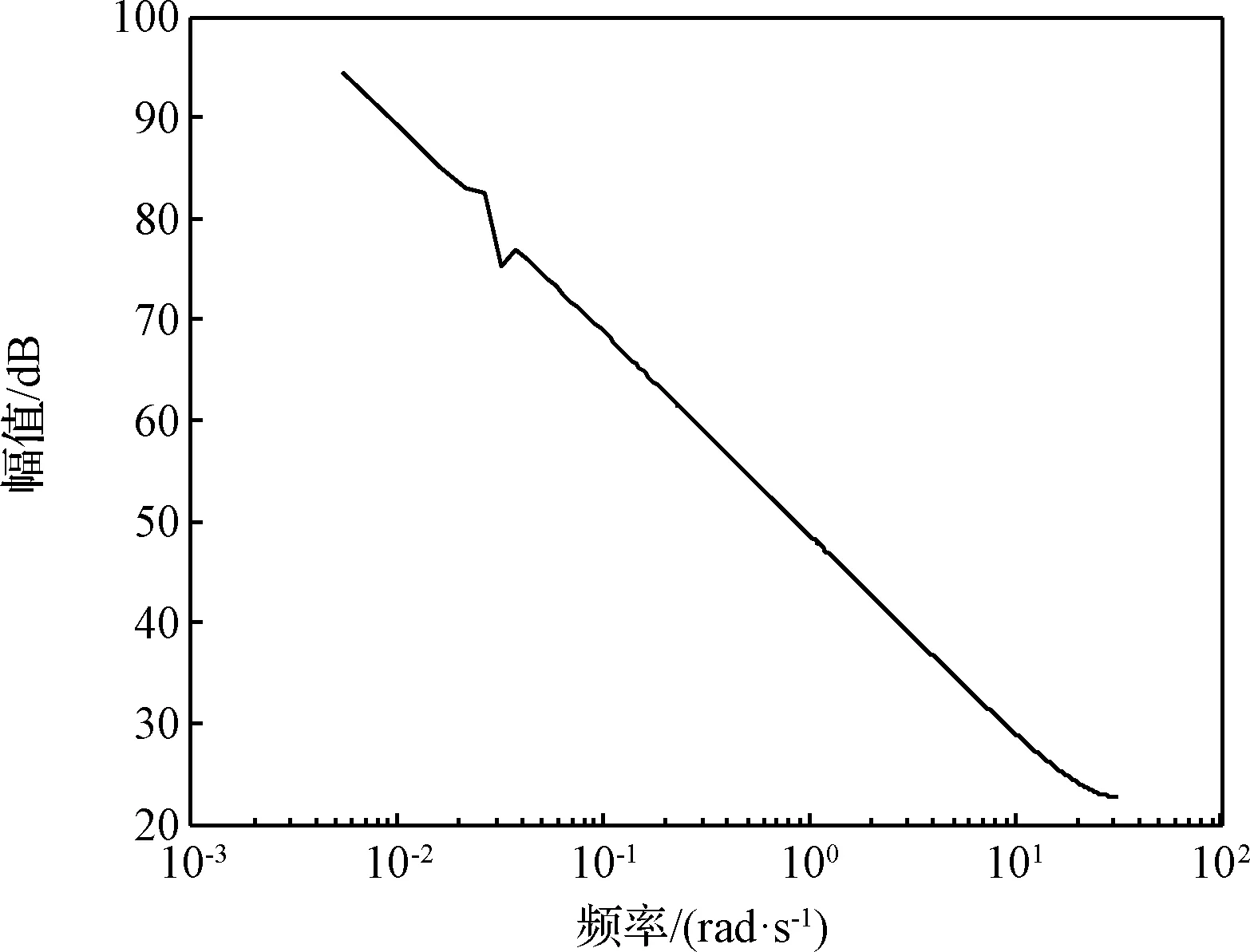
圖2 Welch算法確定地心距信號的譜圖Fig.2 Spectrum of geocentric distance signal via Welch algorithm

采用線性消勢法消除地心距信號的趨勢，經擬合確定的趨勢表述為(單位：m)：

d(n)=6.4235×106-5.8370n

(24)

消除地心距信號中相應的線性項，得到線性消勢地心距信號，如圖3所示。可見信號在0值附近振蕩，且為衰減振蕩，整體仍存在小幅度的非線性趨勢。

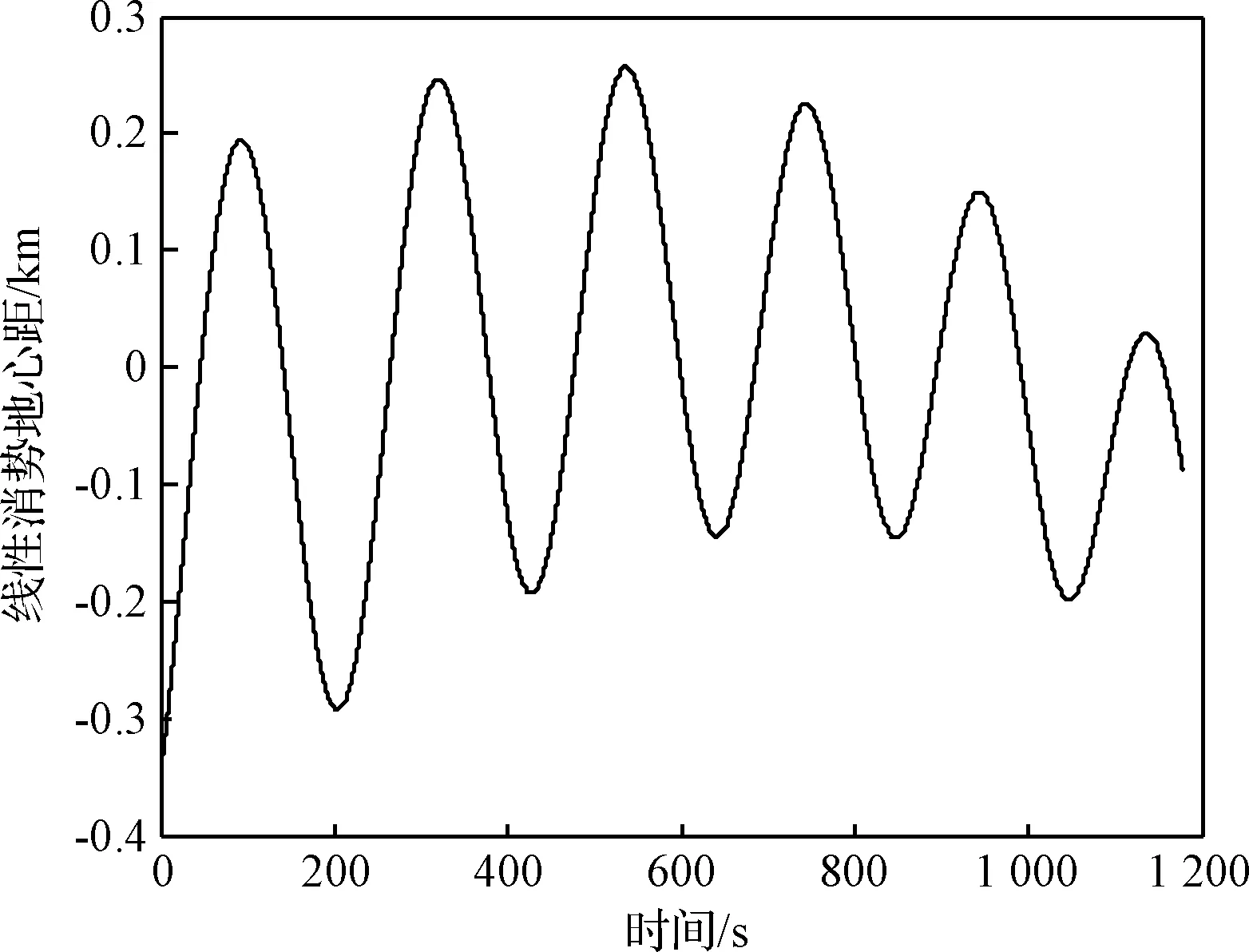
圖3 線性消勢地心距信號時域圖Fig.3 Time domain diagram of linearly detrended geocentric distance signal

使用Welch算法分析線性消勢地心距信號的功率譜，如圖4所示。可見第一峰值頻率為0.032 rad/s、第二峰值頻率為0.02667 rad/s，該頻段集中了大部分能量，在低頻部分存在一個小峰值。對照信號時域圖可知，衰減振蕩即為第一和第二峰值所代表的部分，整體小幅度非線性趨勢即是低頻峰值所代表的部分。

圖4 Welch算法確定線性消勢地心距信號的譜圖Fig.4 Spectrum of linearly detrended geocentric distance signal via Welch algorithm

使用AR模型對線性消勢地心距信號進行功率譜估計。首先，模型階數由1逐步增加并計算AIC，確定AIC最優階數為3，則階數選擇范圍定為2，3，4。下面分別使用這三種AR模型進行功率譜估計，如圖5～7所示，可知線性消勢地心距信號的峰值頻率分別為0.02769 rad/s、0.02894 rad/s、0.01001 rad/s和0.02944 rad/s。

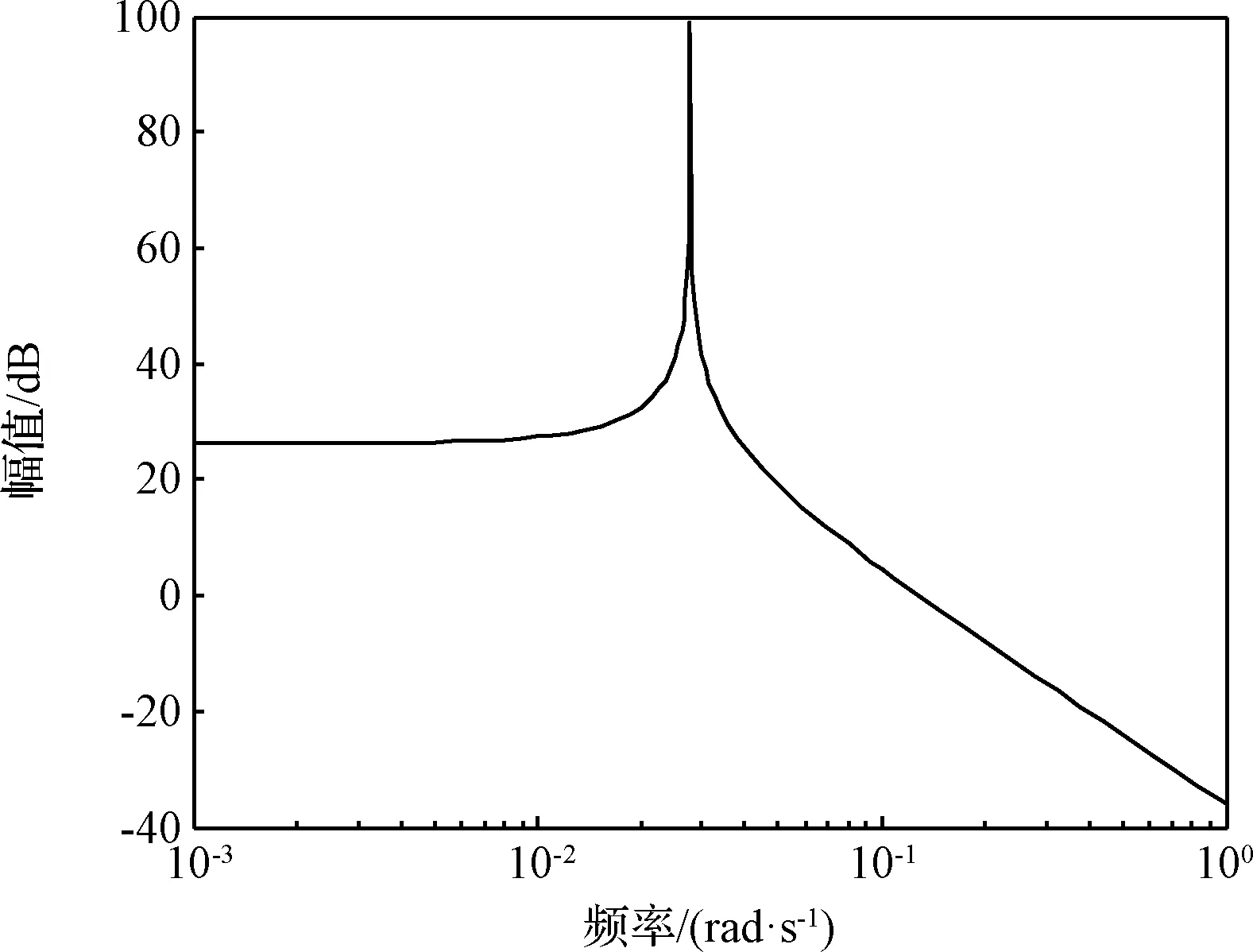
圖5 2階AR模型確定線性消勢地心距信號的譜圖Fig.5 Spectrum of linearly detrended geocentric distance signal via second-order AR model

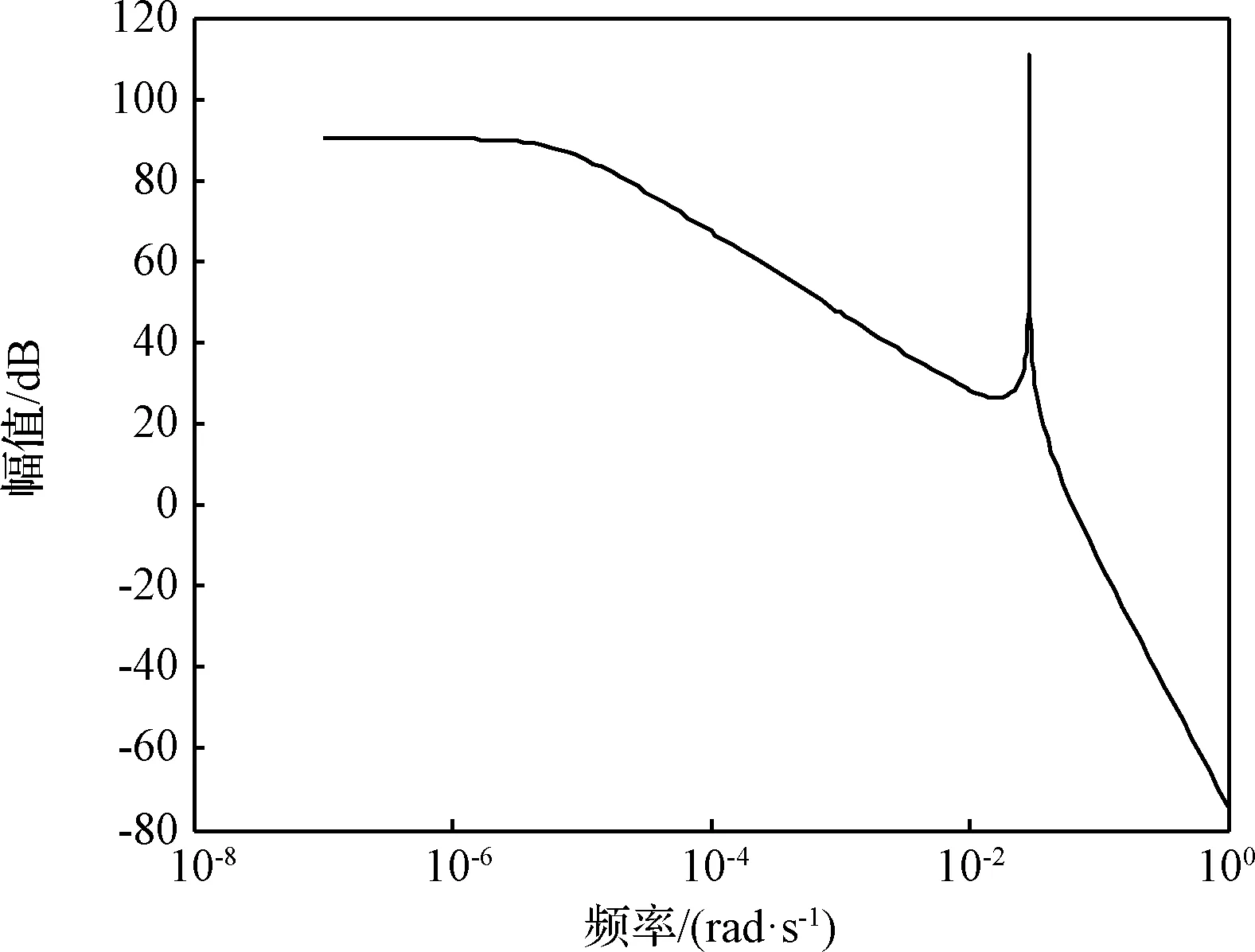
圖6 3階AR模型確定線性消勢地心距信號的譜圖Fig.6 Spectrum of linearly detrended geocentric distance signal via third-order AR model

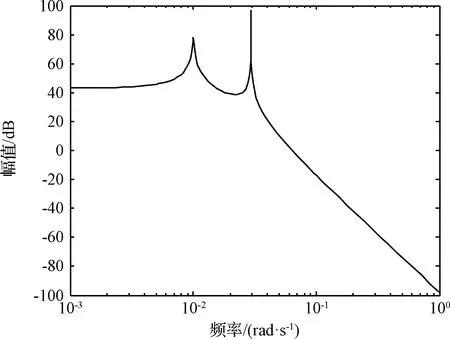
圖7 4階AR模型確定線性消勢地心距信號的譜圖Fig.7 Spectrum of linearly detrended geocentric distance signal via fourth-order AR model

結合時域圖以及Welch算法的譜估計結果可知，線性消勢地心距信號的峰值頻率在0.02667～0.032 rad/s之間，而且在低頻部分存在一個小峰值。2階和3階AR模型均識別出該范圍內的一個峰值，4階AR模型則識別出該范圍內一個峰值和范圍外一個低頻峰值。3階AR模型雖然是AIC最優的，但其低頻部分仍存在較大的能量，因此其對信號的描述是不準確的，其輸出存在低頻漂移。2階和4階模型識別出窄尖峰譜線，對信號的刻畫較為準確。識別得到的線性消勢地心距AR模型分別為(單位：m)：

A(z)x(n)=u(n)

(25)

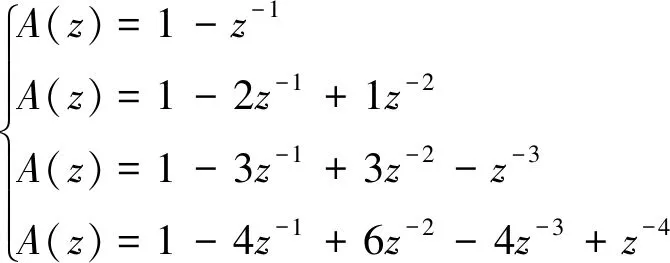
(26)

則完備的地心距模型為經線性補償的AR模型(Linearly compensated AR model，LAR)：

r(n)=x(n)+d(n)=x(n)+

6.4235×106-5.8370n

(27)

下面對上述模型進行校驗，基本思想為：將動力學模型作為參考，考察在相同初始條件下LAR模型輸出與動力學模型輸出的一致性程度；其中LAR模型的輸出稱為LAR數據，動力學模型的輸出稱為參考數據。驗證指標為：以均值和標準差檢驗兩樣本的基本性能參數是否一致；采用秩和檢驗法校驗兩樣本概率分布的一致性[25]。

首先，由動力學模型生成地心距的真實數據，并在相同初始條件下使用上述LAR模型對地心距進行預報，結果如圖8～9所示。可見，1階模型給出的預報結果是線性的，預報誤差隨著彈道的振蕩而波動；2階模型、3階模型和4階模型預報結果都是波動形式，頻率和振幅與動力學模型給出的真實值一致。

然后，考察LAR數據與參考數據的一致性程度，如表1所示。秩和檢驗中，0假設為兩樣本概率分布一致，1假設為不一致。可見1階和3階模型的均值偏離參考值較大，未通過秩和檢驗，這是輸出的低頻漂移造成的；2階和4階模型通過了秩和檢驗，與動力學模型具有較高的一致性，驗證了本文方案的有效性。

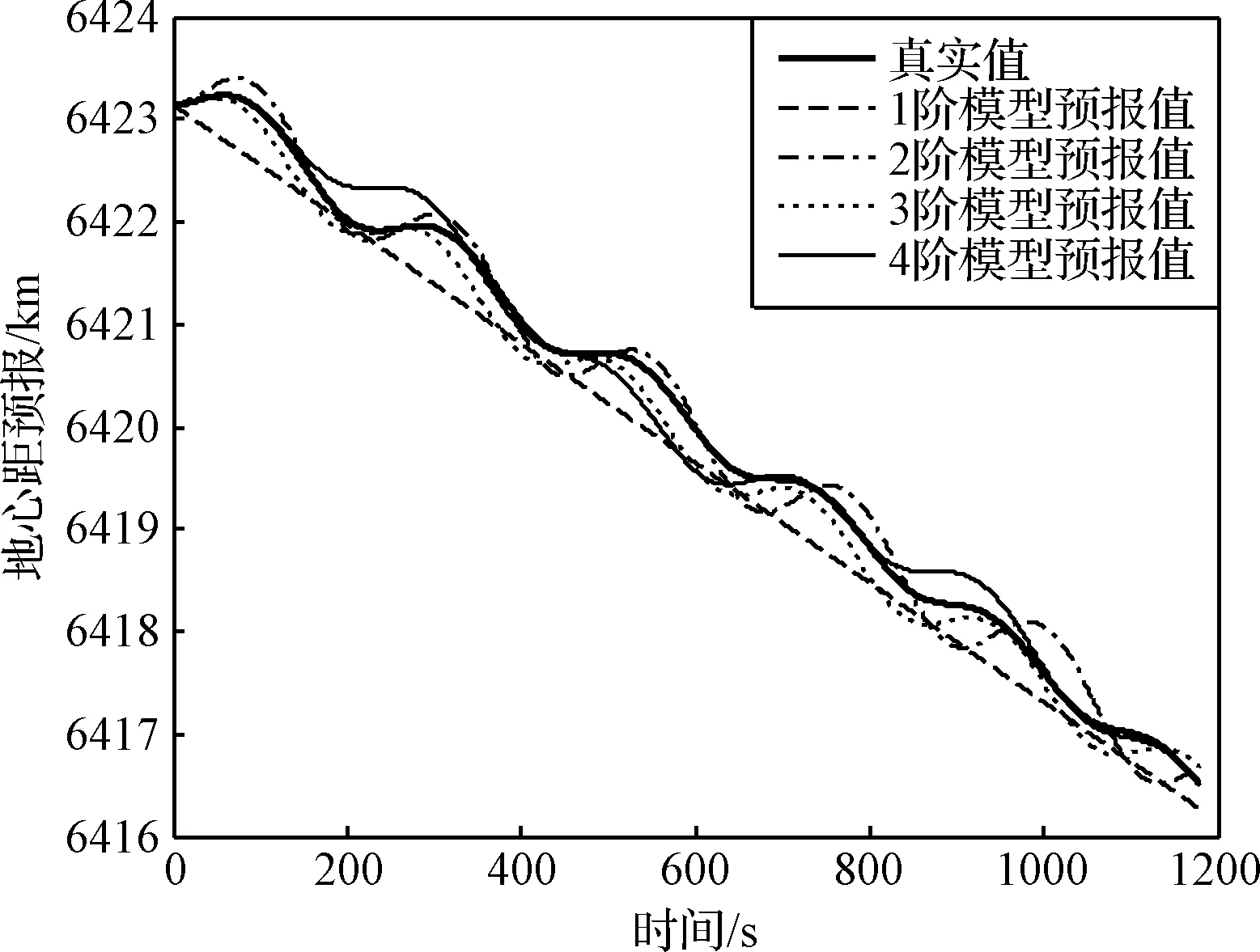
圖8 地心距預報結果Fig.8 Prediction results of geocentric distance

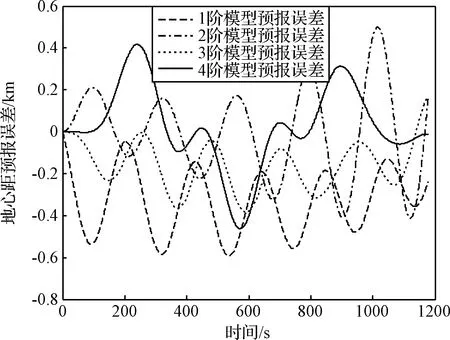
圖9 地心距預報誤差Fig.9 Prediction error of geocentric distance

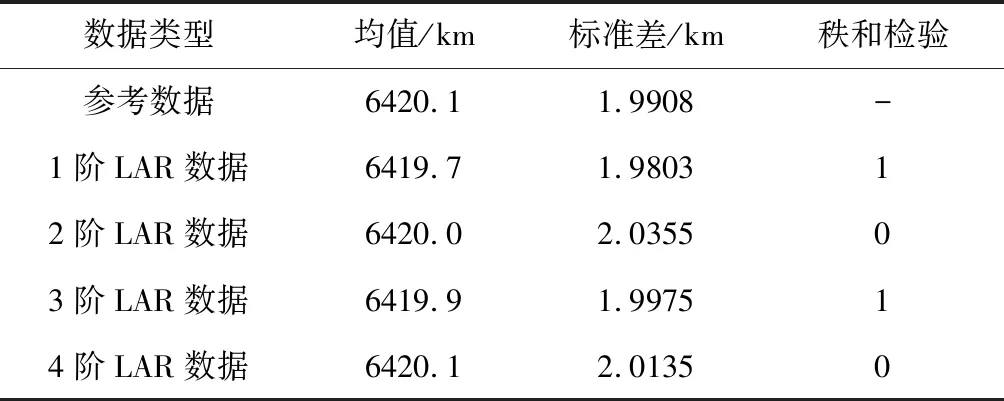
表1 模型校驗結果Table 1 Model validation results

5 結 論

本文綜合運用信號處理領域的經典和現代譜估計理論，對彈道數據進行分析和建模。由Welch算法確定大致的譜圖，然后由AR模型進行精確的功率譜估計，并給出彈道數據的參數化模型。針對彈道數據非平穩特性，本文采用線性消勢法對信號進行消除趨勢操作；針對模型階數選擇準則無法給出確定結果的問題，本文提出綜合經典和現代譜估計的譜圖，確定AR模型的階數。仿真結果表明，針對以線性趨勢為主要趨勢并帶有小幅波動的高超聲速跳躍彈道，以本文方法確定的LAR模型與動力學模型具有較高的一致性。