一類強耦合強不確定性強非線性快時變系統復合控制
孔 雪,寧國棟,楊 明,王松艷,晁 濤
(1. 哈爾濱工業大學航天學院控制與仿真中心,哈爾濱 150080;2. 復雜系統控制與智能協同技術重點實驗室,北京 100074;3. 北京機電工程研究所,北京 100074)
0 引 言
隨著飛行器的跨空域、寬馬赫數范圍飛行,飛行器顯現出強耦合強不確定性強非線性快時變特性,對控制提出了非常高的要求,這類強耦合強不確定性強非線性快時變特性系統的控制問題已成為控制界的最具挑戰性的課題之一[1-10]。
基于強耦合強不確定控制的考慮,滑模控制是一種切實有效的方法[11]。在滑模控制中,系統狀態和系統參數與系統結構無關,僅取決于滑模平面的設計,實現了系統的解耦。滑模控制的最大優點就是系統一旦進入滑模狀態,系統狀態的轉移應不再受系統原有參數變化和外部擾動的影響,對系統參數和外部擾動具有完全的或較強的魯棒性和不變性。基于強非線性快時變控制的考慮,軌跡線性化控制被提出[12],其本質是首先利用被控對象開環的偽動態逆將軌跡跟蹤問題轉化為一個非線性時變的跟蹤誤差調節問題,然后設計閉環的狀態反饋控制律使得整個系統獲得滿意的控制性能。基于智能化的考慮,模糊控制是利用模糊集合理論,把人的模糊控制策略轉化為控制算法,適用于權重調度。
綜合利用滑模控制、軌跡線性化控制、模糊控制,提出一種適用于強耦合強不確定性強非線性快時變的復合控制方法。
1 一種適用于強耦合強不確定性強非線性快時變的復合控制
1.1 問題描述
對于非線性多輸入多輸出系統:
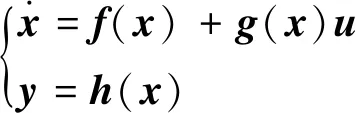
(1)
式中,u∈Rm為輸入,f∈Rn,g∈Rn×m和h∈Rm是狀態變量x∈Rn的光滑有界函數。假定其受一般形式的攝動和外擾,則:
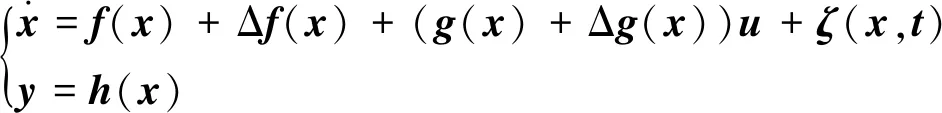
(2)
式中,Δf∈Rn和Δg∈Rn×m為系統攝動,ζ∈Rn為外擾。基于系統跟蹤問題引入以下假設:
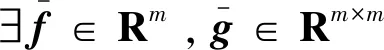
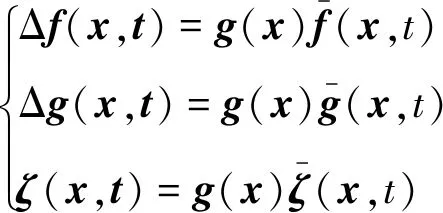
(3)
1.2 基于強耦合強不確定性控制
針對耦合特性具有強不確定性的對象,將子系統間耦合視為干擾,滑模控制(Sliding mode control,SMC)是一種適用的控制方法。為進一步提高強耦合強不確定性的控制能力,采用自適應滑模控制權衡滑模區域大小和滑動模態的響應速度[13],采用滑模狀態觀測器觀測攝動和干擾[11]。但對于滑模控制,存在固有抖振特性,考慮在滑模面附近帶內,選用其它控制方法來彌補SMC的不足。
1)自適應滑模控制
定義1.以PD型滑模面為例,常規PD型滑模面選取如式(4)。式中,e為狀態偏差。定義滑模面斜率為c=c1/c2。
(4)
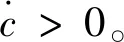
結合滑模控制的基本條件,以二階系統為例,分析c選取原則,結論如式(5)所示,式中,λ1和λ2為系統特征根。
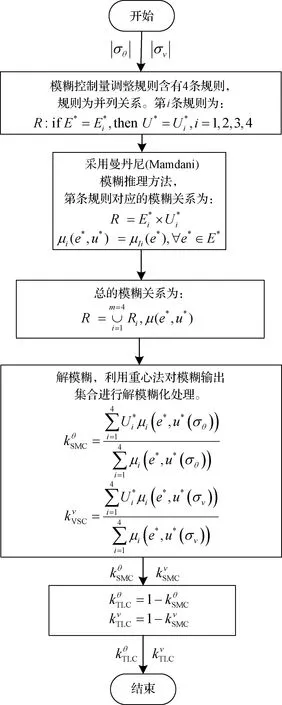
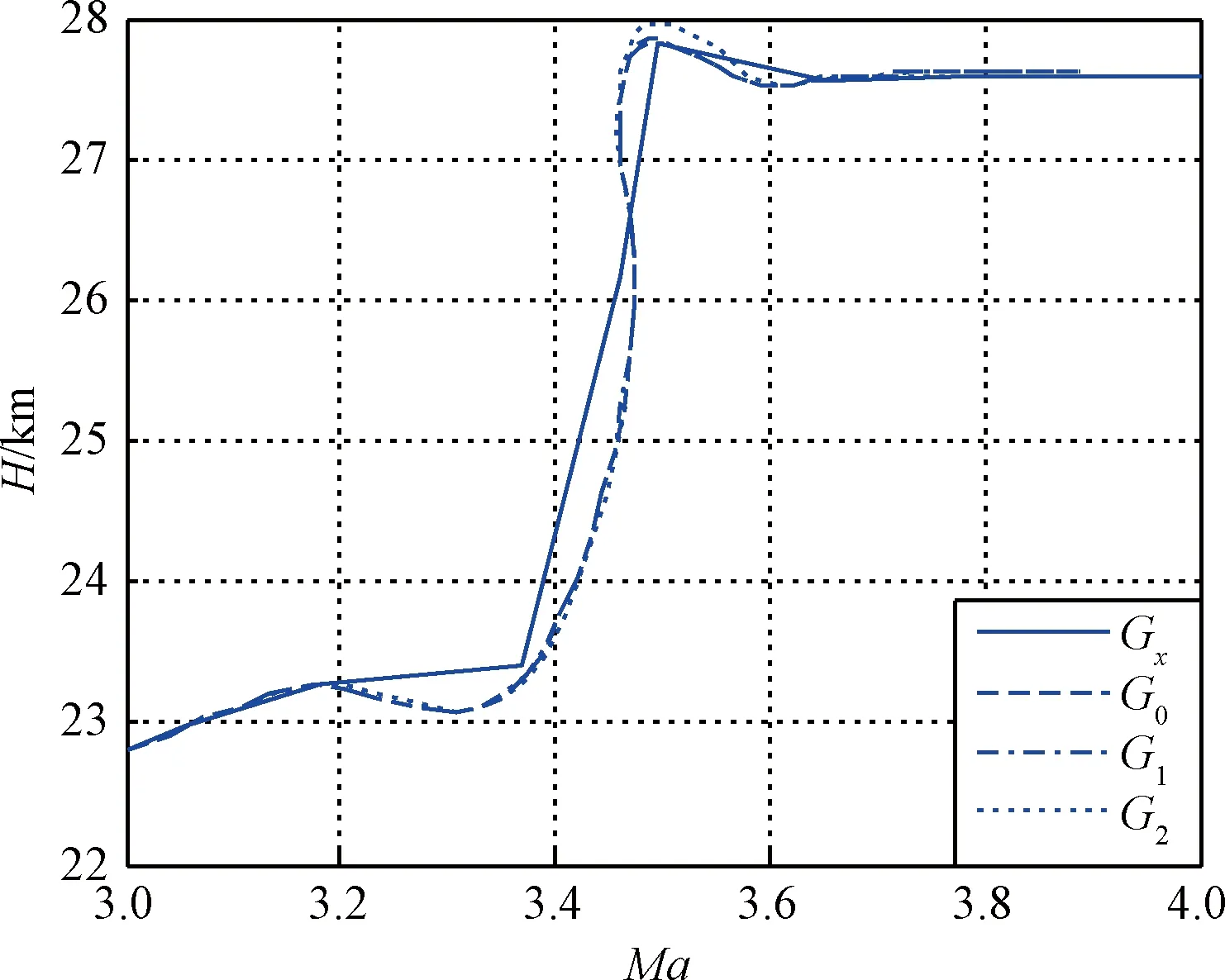
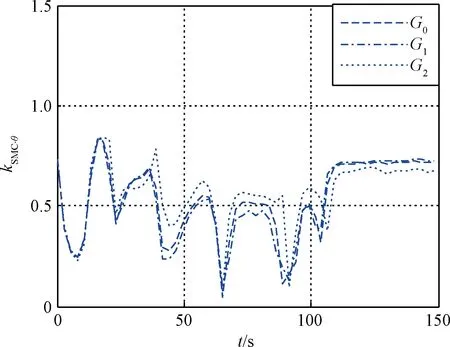
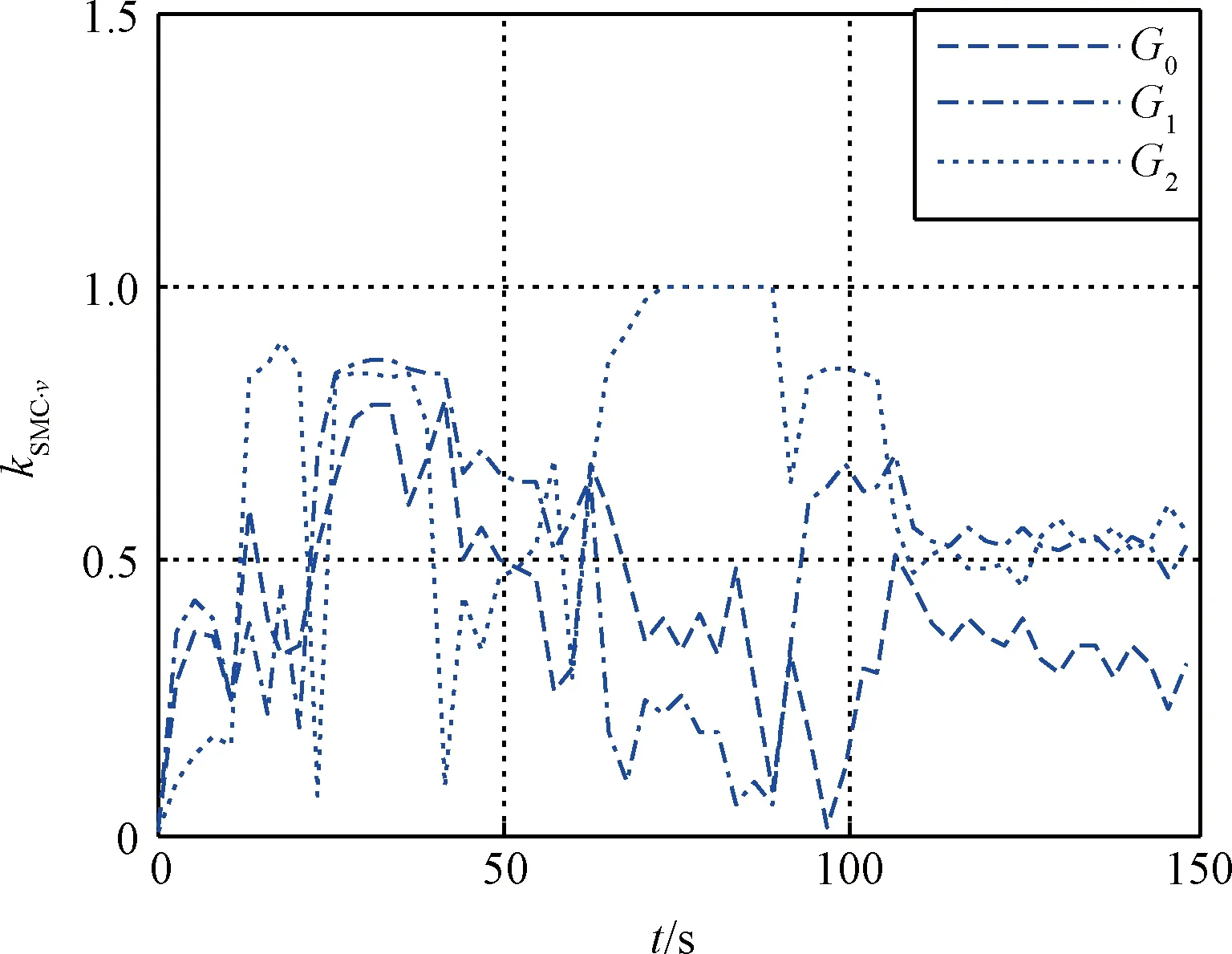
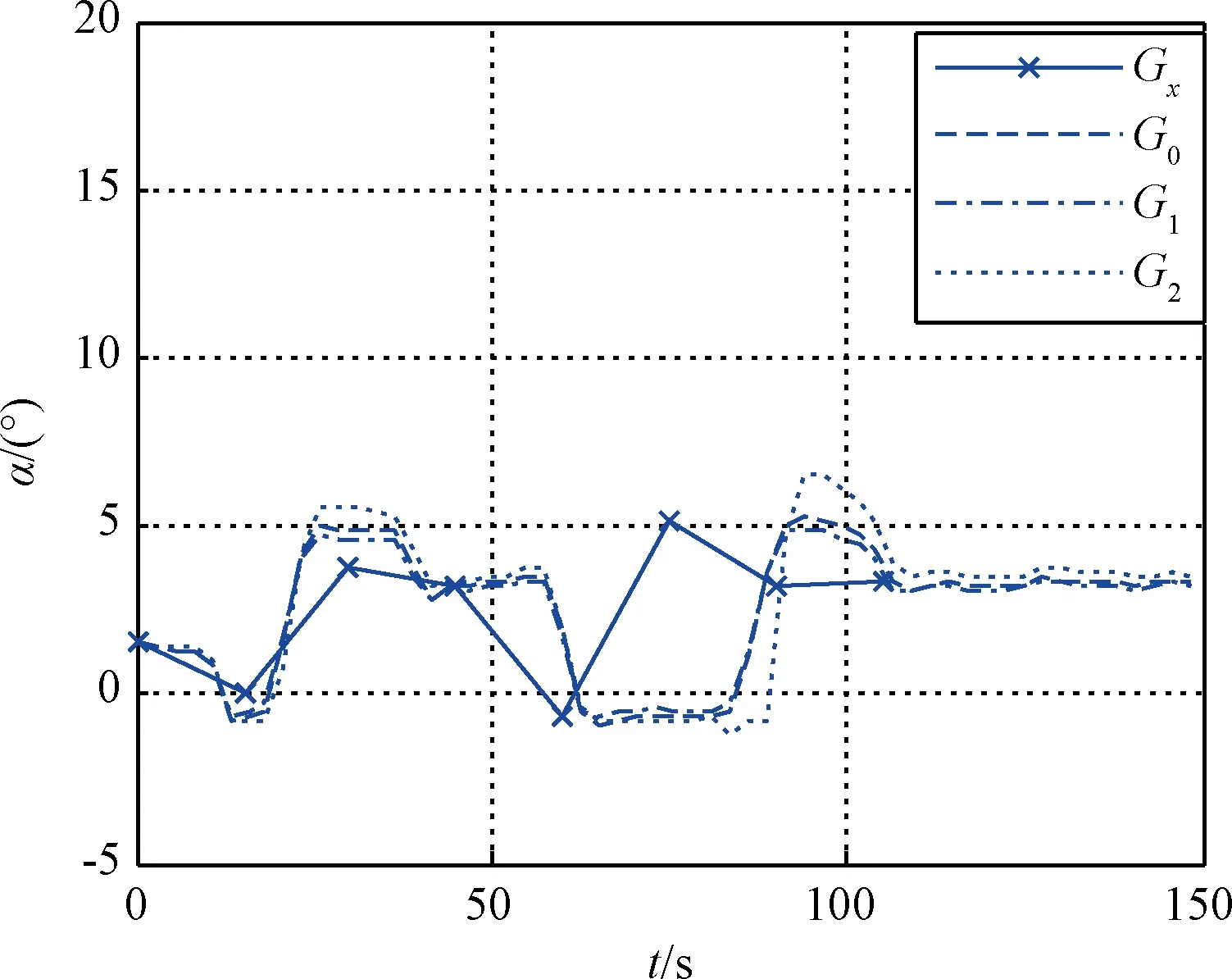
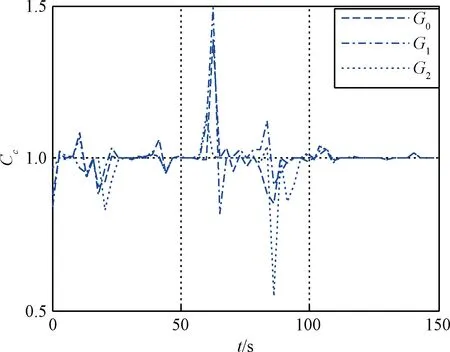
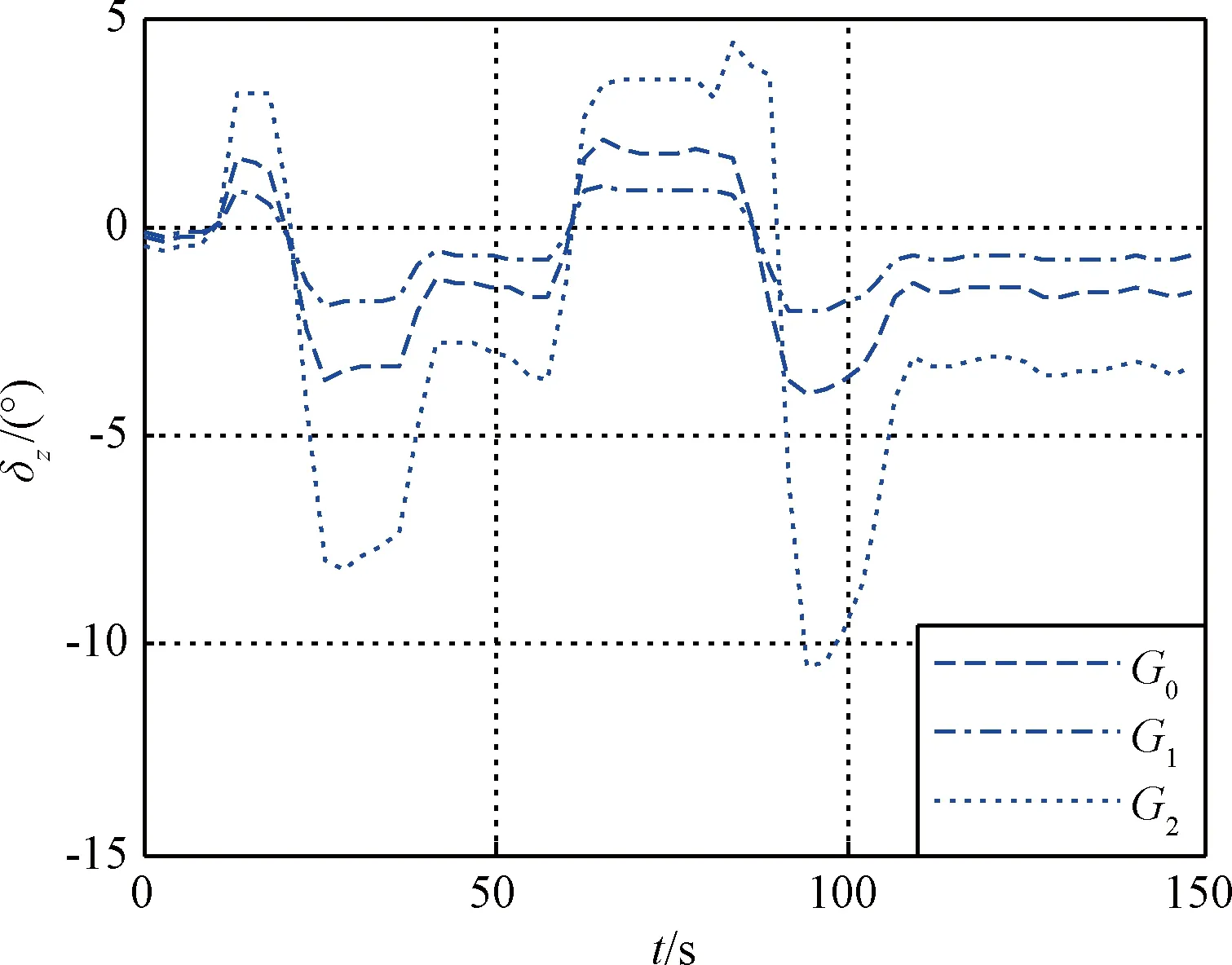
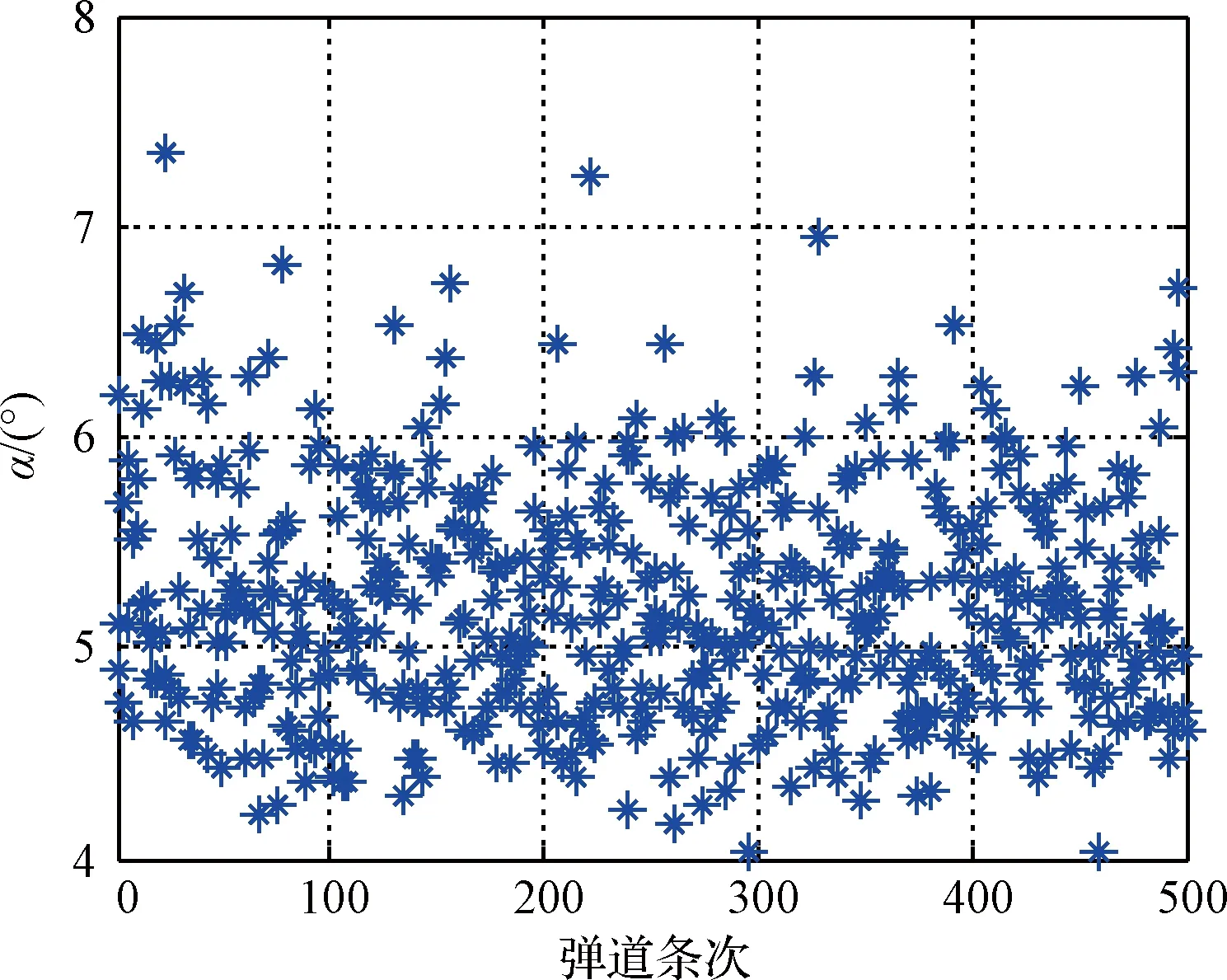
cmax<|λ1|, 0 (5) 仍以PD型滑模面為例,自適應變結構滑模面設計為[5]: (6) (7) 根據e0,結合式(5),給出正實參數ca,cb和cc的范圍,可根據期望的響應特性設置。 2)滑模狀態觀測器 σ可以表示為: (8) (9) 式中,ci·j,?i=1,2,3,…,m,j=-1,0,1,…,ri-2為動態性能待選參數,ei為第i個狀態偏差。 微分式(9)可以得到: (10) 式中, Ξ=Ξ0+ΔΞ=[Ξ1,…,Ξm]T∈Rm (11) (12) 這里Ξ0∈Rm和ΔΞ∈Rm分別為標稱和攝動干擾參量,?i=1,2,3,…,m。式(10)~(12)導數為Lipschitz情況下導數。 假設2.基于控制能力考慮,假設ΔΞ有界: (13) (14) 為了抑制系統抖振,提高系統魯棒性,式中ΔΞ需要通過滑模狀態觀測器(Sliding mode state observer, SMSO)觀測得出。基于Lyapunov第二定理,設計改進型滑模狀態觀測器(Sliding mode district observer, SMDO)如下[11]: (15) 式中,v∈Rm為輔助控制,Γ∈Rm為輔助滑模面,λ=[λ1,λ2,…,λm]T為一常數向量且滿足λi>0,?i=1,2,3,…,m,l=[1,…,m]T為攝動干擾參量的上界。 vi=(|ΔΞi|+λi)sgn(Γi),?i=1,2,3,…,m (16) -λi|Γi|,?i=1,2,3,…,m (17) ?i=1,2,3,…,m (18) (19) 綜上,基于SMDO的SMC控制律為: (20) 軌跡線性化控制(Trajectory linearization control,TLC)是一種非線性跟蹤和解耦控制方法,在解決強非線性快時變參數系統的控制方面具有得天獨厚的優勢,但在穩定性方面卻因為線性化的處理,不能提供足夠的魯棒特性來滿足飛行器在復雜飛行條件下的穩定控制需求,特別地對于存在大量外界干擾和建模誤差且運行條件十分惡劣的實際系統,當系統中不確定性因素足夠大時,TLC方法的控制性能降低甚至失效。 定理2.對于非線性系統,在x0處具有向量相對階{r1,…,rm},則有: r1+r2+…+rm≤n (21) 若r=r1+r2+…+rm=n,系統可以實現完全I/O線性化,原輸出方程可以表示為: y=BF(x)+AF(x)u (22) 根據式,若AF(x)滿秩,可以構建如下的反饋控制律: (23) 使得系統實現輸入輸出的解耦控制。 圖1 TLC方法控制結構Fig.1 The control structure of TLC 誤差跟蹤方程為: (24) (25) 考慮如下線性時變系統: (26) 式中: (27) 假設4.式(27)中的(A(t),B(t))可控。 基于以上假設,可設計線性時變反饋控制器η=K(t)e,使得線性時變系統平衡點e=0為指數穩定,并記Ac(t)=Ae(t)+Be(t)K(t)。式中,Ac(t)是期望的控制回路閉環誤差動態特性,根據PD譜[3]進行設計。根據線性時變反饋控制律η=K(t)e可保證非線性系統在平衡點e=0指數穩定。 四強復合控制是指面向強耦合強不確定性強非線性快時變系統的復合控制。四強復合控制結構如圖2所示,滑模控制(SMC)與軌跡線性化控制(TLC)組合應用,同時引入模糊控制進行雙環調度,實現雙環的權重智能分配。在離滑模面距離較遠時,SMC環占優,充分利用SMC的適用于強耦合及強不確定性控制的優勢,降低TLC的模型依賴性;在離滑模面距離較近時TLC環占優,充分利用TLC的適用強非線性、強時變特性控制的優勢,削弱SMC的抖振效應,保證了工程實際應用的能力[6~11]。 圖2 四強復合控制結構Fig.2 The control structure of four strong characters 四強復合控制設計的步驟可以概括為: 1)在干擾為零時,基于動態逆方法設計標稱控制,基于PD譜理論設計線性時變狀態反饋控制律,使得標稱系統穩定。 2)設計滑模控制器和滑模觀測器,逼近未知干擾,使得閉環系統具有較強的魯棒性,在模型不確性時閉環系統穩定。 3)設計模糊決策,確定雙環控制權重。 錢學森工程控制論中針對復雜系統的工程穩定性分析有如下結論[14]: 1)一般來說,采用Lyapunov方法理論上可以解決穩定性,但在實際工作中這些方法均嫌過于復雜。因為其依賴于系統系數及其基本解的一些深刻的分析特征,后者卻又常常得之不易。因此該類方法沒有在實際工作中得到廣泛應用。 2)若系統的基本解有界,則系統穩定。只需給出n種不同的初始條件,即可求出系統的基本解。借助于主流計算機,基本解的獲取比較容易,即可判別系統穩定性,不需要對系統做任何繁雜的分析。 強耦合強不確定強非線性快時變系統是一種復雜系統,考慮飛行剖面及全系統參數的不確定性,采用蒙特卡洛統計試驗法獲取飛行范圍的基本解,錢學森全系統工程穩定性獲取方法適用于該類強耦合強不確定強非線性快時變系統復合控制的穩定性分析。 飛行器數學模型如式(28)~(30)所示[15]: (28) (29) (30) 式(28)~(30)數學模型為通用數學模型,針對強耦合強不確定性強非線性快時變對象,式中的函數和參數將有所體現。具體分析如下: 1)強耦合特性 發動機與飛行器本體強耦合,主要體現在兩個方面:發動機的附加力矩影響;飛行器姿態對發動機的影響。 2)強不確定特性 包括動力、氣動、大氣、初始狀態、結構參數等多種不確定性。 3)強非線性特性 主要體現在兩個方面:氣動和發動機力學特性的強烈耦合在綜合力學特性上表現為較大的非線性特點;飛行器跨大空域飛行條件下相對于被控對象而言,環境參數如大氣密度、大氣溫度和風場都是非線性變化的,它們不會隨時間或能量等自變量呈線性變化。 4)快時變特性 主要體現在兩個方面:由于跨大空域、跨大速度的飛行軌跡特點,飛行狀態參數,如飛行高度、速度和飛行器質量快速變化;飛行器自身的相關特性也不是固定不變的,主要表現為飛行器所受氣動熱影響效應隨時間增長,相應的結構彈性同氣動的耦合特性也發生變化。 基于四強控制策略的制導控制律結構如圖3所示。圖3中下標c表示指令值。 圖3 基于四強控制策略的制導控制設計Fig.3 Control strategy based on four strong characters 受限于篇幅,這里給出制導回路的部分設計,控制回路設計思路相同。縱向制導律由滑模(SMC)制導環、軌跡線性化(TLC)制導環、模糊(Fuzzy control,FC)制導環復合而成,如式(31)所示。 uzz=kSMCuzz,SMC+kTLCuzz,TLC (31) 1)發動機保護控制SMC制導環 考慮參考軌跡跟蹤及發動機保護需求,設計滑模面如式(32)所示,包括誤差比例積分策略和隔離段激波串有限條件位置積分策略。 (32) uzz,SMC= (33) (34) (35) 2)TLC制導環 TLC制導環由偽動態逆控制器和線性時變調節器兩部分組成。令系統攝動為零,可知制導回路系統的相對階為2,可通過動態逆求得制導回路的控制輸入: (36) 設計PI狀態反饋控制律: (37) kzz(t)=[RzzBzz(t)]-1Rzz[Azz·c(t)-Azz(t)] (38) 式中:Rzz為常數陣,定義如式(39)所示,Azz為系統增廣后狀態方程,Azz·c為期望閉環方程。 (39) 綜合式(36)和(39),可得TLC制導環控制為: (40) 3)智能權重調度策略 模糊調度流程如圖4所示。 圖4 模糊控制流程圖Fig.4 The flow chart of fuzzy control 依據飛行器的數學模型,對所設計的基于四強控制策略的制導控制律進行數值仿真,仿真中加入靜穩定度和舵效攝動,校驗其魯棒性。仿真條件詳見表1。 表1 仿真條件Table 1 Description of simulation conditions 圖5和圖8中下標x表式參考軌跡,飛行任務為速度由Ma3加速至Ma4,高度由22.8 km爬升至27.6 km,該飛行任務跨空域、寬馬赫數范圍飛行,具備強耦合強不確定性強非線性快時變特征。利用基于四強控制策略的制導控制律得出的系統跟蹤結果如圖5~10所示。 圖5 馬赫數高度曲線Fig.5 Curve of height vs Mach 圖6 kSMC·θ隨時間變化曲線Fig.6 kSMC·θ vs time 圖7 kSMC·v隨時間變化曲線Fig.7 kSMC·v vs time 圖8 攻角隨時間變化曲線Fig.8 Angle of attack vs time 圖9 飛推耦合度因子隨時間變化曲線Fig.9 The coupling factor for aircraft and scramjet vs time 圖10 升降舵偏轉角隨時間變化曲線Fig.10 Elevator rudder deflection angle vs time 從制導指令跟蹤情況來看,基準彈道及攝動彈道均可精確跟蹤參考軌跡的馬赫數高度剖面,通過精確跟蹤,可以滿足馬赫數、動壓、熱流約束要求,且為控制實現留有余量。根據kSMC·θ和kSMC·v隨時間變化可知,SMC環和TLC環的控制切換權重隨不確定性設置發生變化,且變化趨勢與飛行器的狀態密切相關。 從控制指令跟蹤情況來看,基準彈道及攝動彈道攻角及攻角變化率滿足約束要求。 飛推耦合度因子Cc,定義如式(41)所示。該因子表征飛推力矩耦合程度,其數值越大,則耦合程度越強。 (41) 根據飛推耦合度因子隨時間變化可知,發動機附加力矩占比較大,且其大小與飛行器的狀態密切相關,對飛行器姿態控制提出了較高要求。對于基準彈道攻角可精確跟蹤攻角指令,對于攝動彈道,隨著舵效減小,靜穩定度增大,攻角跟蹤精度變差,當攝動程度為30%時,攻角跟蹤精度在0.5°以內,同時舵面偏轉角度增大。 考慮初始狀態散布,同時附加發動機推力、附加力矩、飛行器升力阻力、壓心及舵效不確定性,進行500條次蒙特卡洛仿真,統計飛行過程中約束滿足情況,最大過載變化范圍[-1, 3.3]g,最大攻角變化范圍[4, 7.3]°,角速率變化范圍[-0.4, 2.7]°/s。受限于篇幅,給出最大攻角散布示意圖,如圖11所示,飛行范圍內基本解有界,采用錢學森全系統工程穩定性獲取方法可證明飛行范圍內的穩定性。 圖11 蒙特卡洛彈道最大攻角散布Fig.11 The max angle of attack spread 隨著飛行器的跨空域、寬馬赫數范圍飛行,飛行器顯現出強耦合強不確定性強非線性快時變特性,對控制提出了非常高的要求。單一控制方法難以兼顧全部控制需求,提出一種該復合控制方法,由三個核心模塊組成,依次為強耦合強不確定性控制模塊、強非線性快時變控制模塊、智能調度模塊。強耦合強不確定性控制模塊采用自適應變結構和滑模觀測器策略,強非線性快時變控制模塊采用軌跡線性化策略,智能調度模塊采用模糊策略。以一具備典型四強特征的飛行器為例,進行了對象四強特性分析,在此基礎上采用四強復合控制方法設計了制導律和控制律,仿真結果表明,該方法有效、可靠,采用錢學森全系統工程穩定性獲取方法可證明飛行范圍內的穩定性。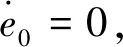
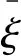
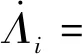
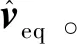
1.3 基于強非線性快時變控制
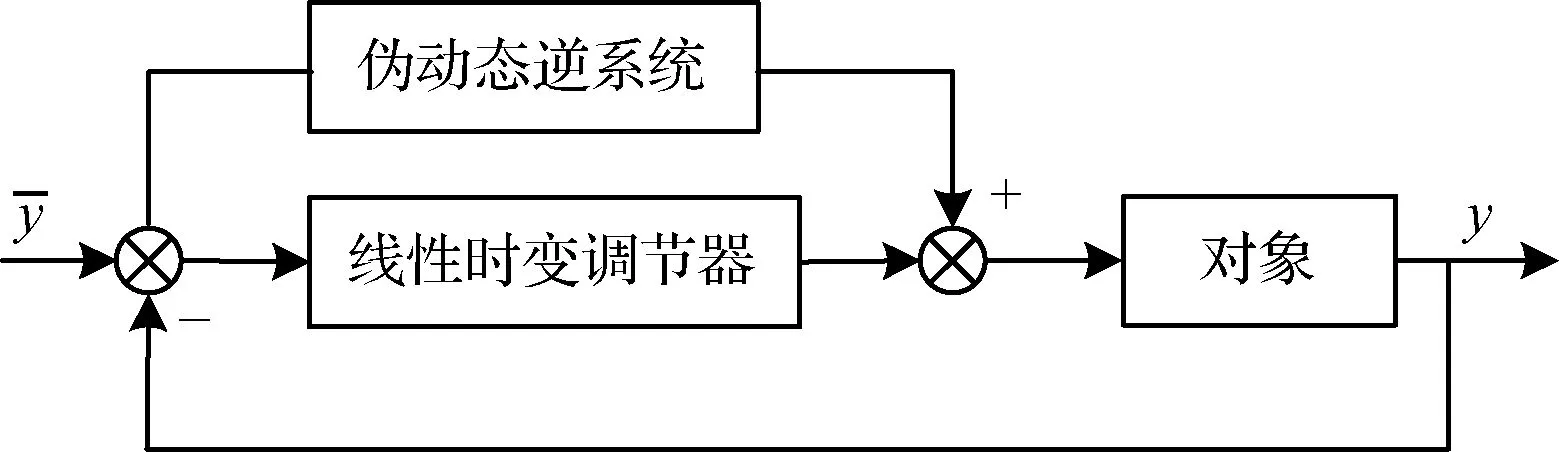
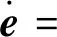
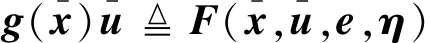
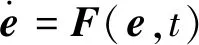
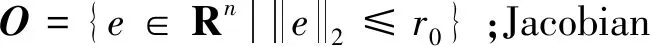
1.4 四強復合控制
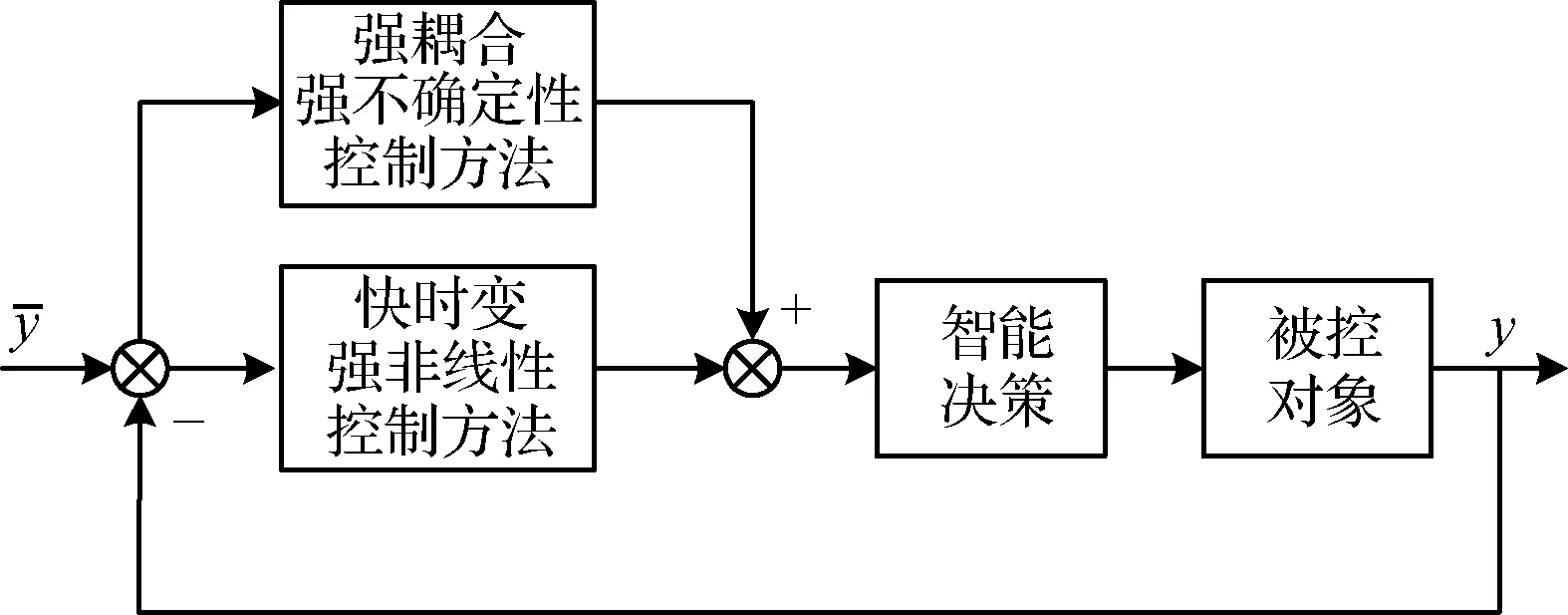
2 典型強耦合強不確定性強非線性快時變飛行器控制
2.1 對象模型
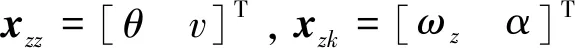
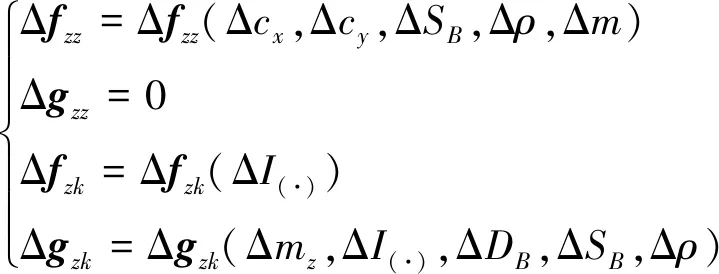
2.2 對象特性分析
2.3 四強復合控制設計
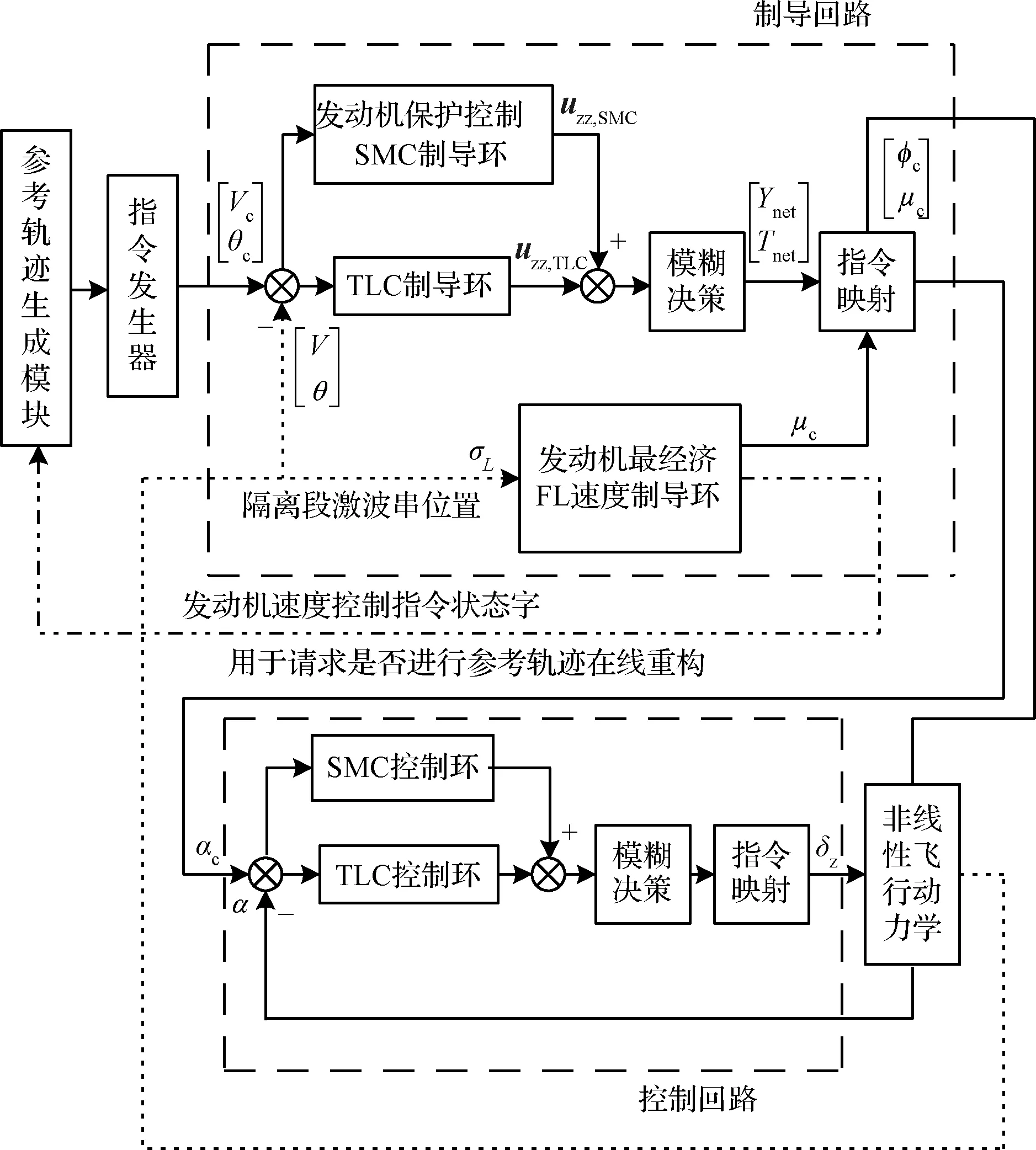
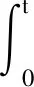
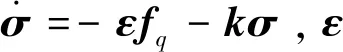
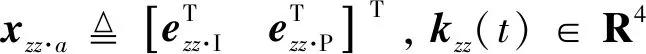
3 仿真校驗

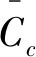
4 結 論

