旋轉導彈等效合力在線自適應補償方法研究

李慶波，陳 釗，謝文龍

(上海機電工程研究所，上海 201109)

0 引 言

旋轉導彈通常采用單通道控制，通過操縱一對舵面作與彈旋同頻率的正弦偏轉運動或者等幅不等寬的偏轉運動，從而產生具有一定大小和方向的等效合力，實現對導彈飛行的控制[1]。由于彈體自旋及舵系統的慣性作用，舵面實際產生的等效合力的方向發生變化，導致控制上在俯仰和偏航通道存在耦合，從而影響彈體的制導控制精度，甚至會引起彈體飛行的錐形擺動和發散。另外，由于舵系統的機械慣性及控制電機驅動能力的限制，使得實際舵偏不能準確跟隨輸入指令的變化，影響等效合力的大小。

目前旋轉導彈解耦的研究和實踐主要有基于指令補償解耦為代表的靜態解耦和基于現代控制為基礎的動態解耦[2]。靜態解耦屬于開環補償方法，在早期的旋轉導彈設計過程中，對于采用等幅不等寬氣動舵機的控制方式，采用了扭角補償技術實現解耦[1]，即舵面逆著彈旋方向扭一個機械轉角，在空間上實現固定的相位超前角度，一定程度上彌補因舵機慣性等導致的相位滯后。對于采用正弦電動舵機的控制方式，通過頻率掃描方法，能夠獲得舵機的相位滯后隨輸入頻率的變化規律，飛行過程中再根據當前的彈體轉速與指令大小，進行超前補償。動態解耦可分為反饋解耦和自適應解耦兩類，基于反饋思想的解耦方法主要有：狀態反饋解耦、輸出反饋解耦、多變量頻域對角占優設計方法等[3-7]；自適應解耦是針對外部不確定性擾動，通過附加控制技術(如增益調度等)來保障其魯棒性和自適應能力,如Sieberling等[8]提出的增量式非線性動態逆魯棒飛行控制方案，則是通過增加角加速度反饋來提升系統的魯棒性。動態解耦通常是從自動駕駛儀的角度進行解耦，即對舵系統的控制耦合進行解耦，同時也能實現對馬格努斯效應和陀螺效應引起的運動耦合[9]進行解耦。

靜態解耦方法由于其實現簡單，在工程中被廣泛應用，該類解耦方法能夠實現某一特定環境下的相位補償，但靜態解耦是一種開環超前補償，因此針對飛行全程中轉速、鉸鏈力矩、指令大小存在較大變化的情況，無法實現準確控制相位補償；動態解耦在理論上的解耦能力具有明顯優勢，但該類解耦方法或是由于嚴重依賴于精確模型而導致補償效果不佳[10]，另外動態解耦依托于自動駕駛儀平臺，而旋轉導彈通常為開環控制，本身就不具備搭載自動駕駛儀的硬件條件。因此雖然開展了一定的理論研究，但工程應用受限。另外，上述的解耦方法均是對俯仰和偏航通道的控制解耦，其作用效果是完成對等效合力控制方向的補償，而對于等效合力大小的補償目前缺少相應的手段，只能通過提高舵系統的工作性能來減小舵系統的指令跟隨偏差。

旋轉導彈的制導控制真正關注的問題是舵系統輸出的等效合力與期望的等效合力是否一致。研究從等效合力的一致性出發，避開基于模型的設計方法，簡化設計過程，提出一套自適應的補償方案及相應的算法，工程實現簡單，同時又能滿足制導控制設計要求。

1 旋轉導彈控制特點

1.1 旋轉等效合力原理

旋轉導彈通常采用與彈旋同頻的高頻正弦信號或等幅不等寬的方波信號[11]控制舵面偏打，利用旋轉一周產生的等效合力實現對導彈過載大小和機動方向的控制。研究以正弦控制的旋轉導彈為例，進行等效合力原理分析及后續的算法設計，對于方波控制的旋轉導彈，該算法同樣適用。下文將介紹旋轉導彈等效合力控制機理[1]。

假設舵軸與彈體z軸重合，舵面作與彈旋同頻率的正弦偏轉運動，則舵偏角δ為：

δ=δ0sin(wDt+θ0)

(1)

式中：δ0為舵偏幅值，wD為彈旋角速度，θ0為舵控信號初相角。

舵偏角在準彈體坐標系下的分量滿足：

(2)

式中：δy,δz分別為在準彈體y向和z向上的舵偏分量。

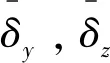
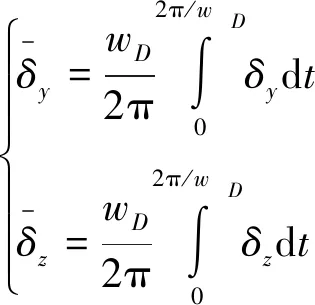
(3)

將式(1)和式(2)代入式(3)，可解得：

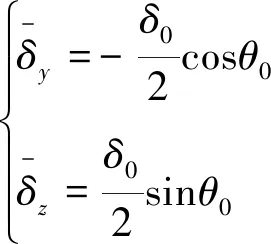
(4)

該等效舵偏產生的等效氣動力為一周等效合力，其對應的等效合力可表示為：

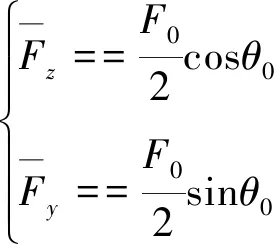
(5)

式中：F0為舵偏幅值等于δ0時產生的氣動力。

等效合力用極坐標表示時，則為：

(6)

旋轉導彈通常采用KK系數是表征舵面所產生的等效控制力大小和方向。上式用KK系數表示為：

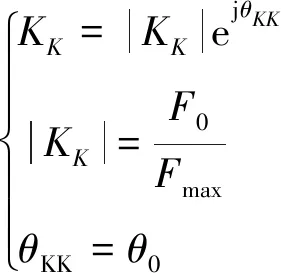
(7)

式中：|KK|為KK幅值，θKK為KK相位，Fmax為最大舵偏角對應的等效控制力。

1.2 相位滯后及幅值衰減機理

旋轉導彈轉速通常較高，因此其控制信號為高頻正弦信號。由于舵系統的電氣通信時延及機械慣性滯后等特性，正弦的舵控指令在經過舵系統并轉化為舵偏角的過程中，信號的幅值和相位會產生畸變。下文以線性二階系統為例展開分析說明[12]。

設舵系統的傳遞函數為：

(8)

式中：Ts為時間常數，ξs為阻尼系數，s為微分算子。

設彈體旋轉角速度為wx，則舵系統的輸入指令信號為：

uin=δ0sin(wxt+θ0)

(9)

通過計算可以得到，輸入指令信號經過舵系統環節后，其輸出信號為：

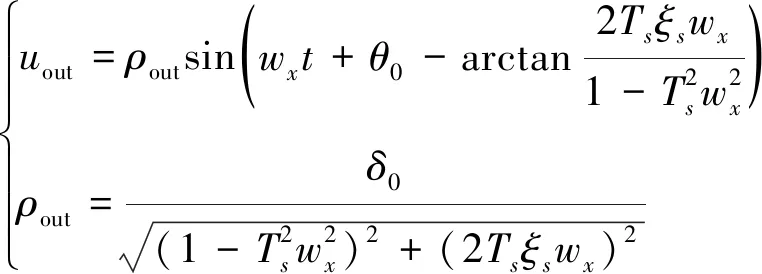
(10)

式中：ρout為舵系統輸出幅值。

通過式(10)可知，正弦信號在通過慣性環節時，其幅值和相位均發生變化。而在實際工作過程中，除了機械慣性環節外，通信延遲、外部負載變化及舵系統的非線性特性等均會引起輸出信號與輸入信號在相位及幅值上的變化。

控制信號相位的變化會引起導彈飛行過程中俯仰通道與偏航通道的耦合，且耦合程度通常在10°～25°左右，因此需要補償相位的方式完成控制解耦。

幅值的變化會引起控制系統前向增益的變化，旋轉導彈通常采用開環控制，增益變化將對整個制導控制系統的導航比產生直接影響，最終影響制導精度。

1.3 傳統補償方式

在導彈實際飛行過程中，舵系統實際的幅值受到飛行氣動負載、機械慣性超調、舵控指令輸入及舵系統產品自身差異性等多個因素的影響，難以對幅值增益的放大或衰減規律進行建模，因此無法開展有效的幅值補償，只能通過提高舵系統的工作能力來一定程度減小這方面的偏差。

舵控指令通過舵系統后，通信時延、機械慣性等主要因素均會導致控制信號相位滯后，因此舵控相位變化具有一定的統計規律性。傳統旋轉導彈采用的相位補償主要采用扭角補償和隨彈體轉速變化的線性補償兩種方式。

早期的旋轉導彈設計中，對于采用等幅不等寬氣動舵機的控制方式，采用了扭角補償技術實現解耦，即舵面逆著彈旋方向扭一個機械轉角。扭角補償能夠在空間上實現固定的相位超前角度，但由于導彈飛行過程中轉速及負載鉸鏈力矩等影響因素的不斷變換，使得扭角補償技術難以實現飛行全程的相位準確補償。

仍以式(8)中的舵系統為例，對基于轉速進行相位補償的機理展開說明。通過式可知，舵系統的相位滯后為：

(11)

舵機時間常數Ts通常是一個很小的值，因而上式可簡化為：

Δθ≈arctan(2Tsξswx)≈2Tsξswx

(12)

由式(12)可知，舵系統相位滯后與轉速呈現近似線性關系，因此可以通過利用轉速擬合的方式進行舵系統相位補償。對于采用正弦電動舵機的控制方式，通過頻率掃描方法，能夠獲得舵機的幅值衰減與相位滯后隨輸入頻率的變化規律，飛行過程中再根據當前的彈體轉速與指令大小，進行超前補償，這種方法能夠實現某一特定環境下的幅值與相位補償，但對飛行全程中轉速、鉸鏈力矩、指令大小存在較大變化的情況，無法實現準確補償，特別是當舵系統時間常數較大(帶寬不足)或是舵系統具有顯著非線性特性的條件下，補償的準確性將大幅降低。

1.4 工程實際問題

實際舵機模型與理論數學模型存在一定差異，舵面負載及控制指令的變化均會導致舵機特性發生變化，從而影響相位滯后關系。下文通過計算某舵系統實測數據，分析相位滯后的影響因素及變化關系。

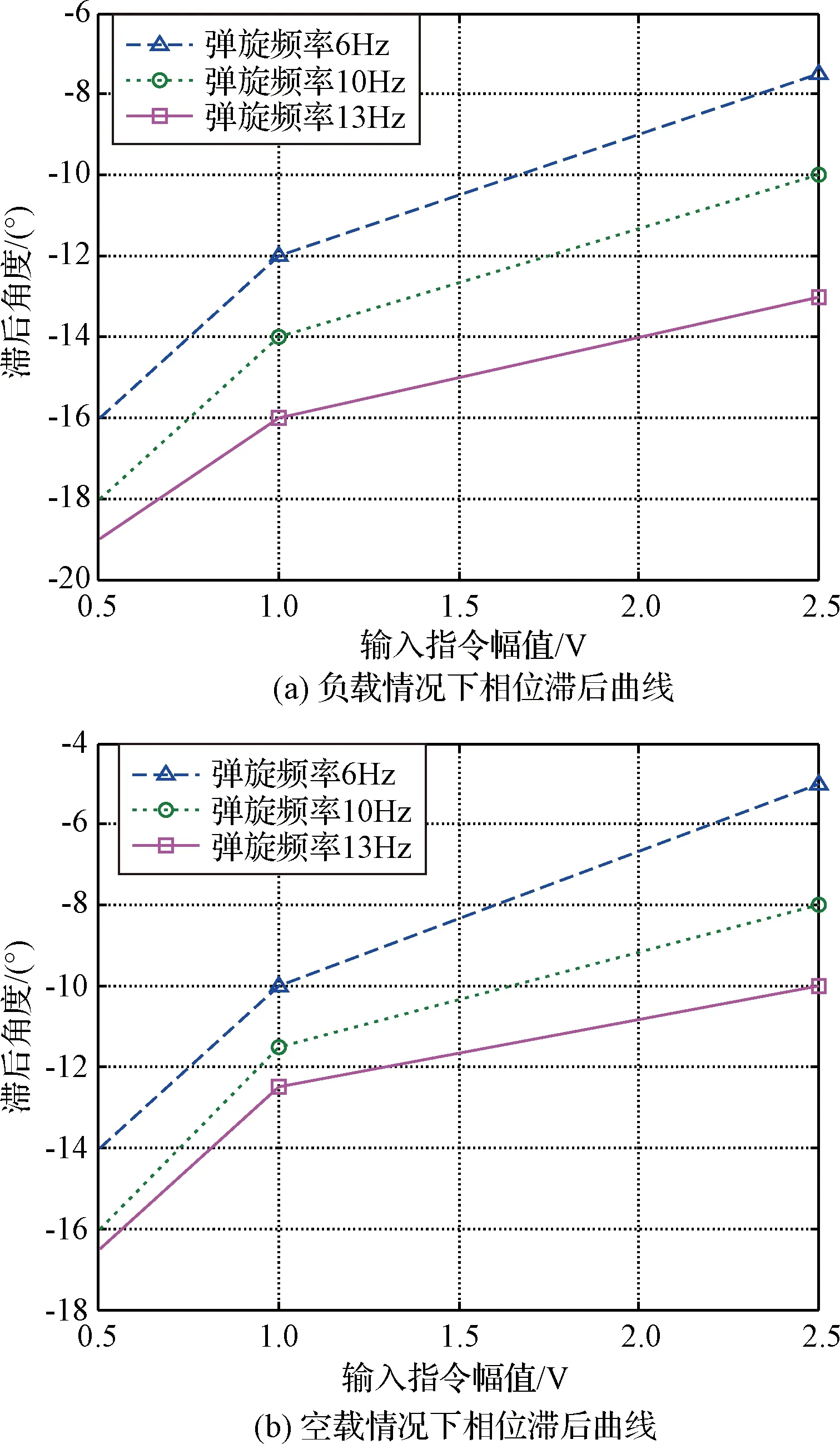
圖1 舵系統相位滯后實測數據圖Fig.1 Test data diagram of rudder system phase lag

分析圖1可以得到以下結論：

1)在輸入指令、舵面負載相同的條件下，舵系統相位滯后隨彈旋頻率的增大而增大，且呈現非線性變化的趨勢。

2)在彈旋頻率、控制指令相同的條件下，負載比空載條件下的相位滯后嚴重。

3)在彈旋頻率、負載條件相同的條件下，控制指令越小，相位滯后越嚴重。

舵控幅值變化同樣受到多種因素的影響，此處不再贅述。

2 等效合力在線自適應補償算法

從旋轉導彈控制機理的角度來看，真正決定導彈控制力方向和控制力大小的因素是舵系統的一周等效合力，而非舵系統的瞬時響應特性，因此等效合力的輸出性能才是旋轉導彈舵系統最為本質的問題。

根據旋轉導彈的控制特點，提出一種基于等效合力的自適應補償方法，即：通過在線計算舵系統等效合力輸出，與期望等效合力做差后形成閉環反饋，通過一定的算法實現自適應補償，從根本上滿足旋轉導彈對舵系統的輸出需求。

2.1 算法設計原則

補償算法設計的目的是解決工程實際中遇到的難題，因此在算法設計過程中應結合現實需求[13-14]，首先確立算法設計的基本原則如下：

1)當彈體轉速突變時，要求能夠快速補償，且過渡平穩。一方面，在旋轉導彈飛行過程中，特別是在起控段，導彈轉速會在短時間內經歷先降低后增大的變速變化，因而舵機的滯后特性也會劇烈變化，如果補償不夠及時或是補償存在多周期反復超調，都會影響飛行控制精度；另一方面，旋轉導彈通常應用于末端打擊和攔截，作戰飛行時間往往只有幾秒到十幾秒，因而對快速性有較高的要求。

2)在外部環境平穩的情況下應能完全消除靜差，實現零相角滯后。巡航段導彈飛行速度快，機動能力強，該飛行段內導彈的耦合程度對制導精度的影響至為關鍵。巡航段內，導彈飛行速度平穩、彈體轉速變化小，因而如何能夠在平穩的外部環境中實現完全解耦關系到制導控制的整體性能。

3)補償算法應具有較強的魯棒性。導彈飛行過程中，控制指令及舵面負載的變化均對信號的幅值和相位帶來不確定性干擾，因此要求補償算法具有較強的抗干擾能力。

4)補償算法應簡單、可靠且具備工程實現的條件。

2.2 等效合力幅值自適應補償算法設計

要實現舵系統俯仰通道與偏航通道的完全解耦，則要保證無相位滯后。根據等效合力的原理可知，欲使舵控相位滯后為零，則要求舵系統輸出信號和輸出信號的KK相位(θKK)相等。根據控制的基本思想[15]，可將輸入和輸出信號的θKK之差作為偏差信號形成反饋控制回路，通過設計合適的補償控制算法，從而對相位進行在線超前補償。設計補償算法如下：

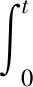
(13)

通過式(13)可知，本文采用了PI控制的思想對控制相位環節進行在線補償。其中比例環節可以實現對誤差的快速消除，能夠快速補償導彈起控過程中彈體轉速突變或飛行過程中舵面負載突變導致的相位滯后；積分環節能夠保證導彈巡航飛行過程中相位的準確控制。

2.3 等效合力幅值自適應補償算法設計

KK幅值補償的目的是保證輸出等效合力與輸入等效合大小一致，據此將輸入輸出等效合力大小之差作為反饋，設計幅值補償算法。

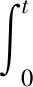
(14)

式中：Δ|KK(t)|為輸入信號與輸出信號的|KK|幅值之差。

幅值補償算法的設計原理與相位補償算法類似，通過比例環節快速消除誤差，通過積分環節使得穩態誤差為零。

2.4 等效合力在線自適應補償算法實現

假設舵系統的傳遞增益為Kdj，則期望舵系統實際輸出與制導控制指令滿足如下關系：

Udjf(t)=KdjUdjk0(t)

(15)

式中：Udjk0為制導控制指令，Udjf為舵系統的實際輸出。

設經過補償后的舵系統控制指令為Udjk，則相位補償和幅值補償算法的原理框圖如下：

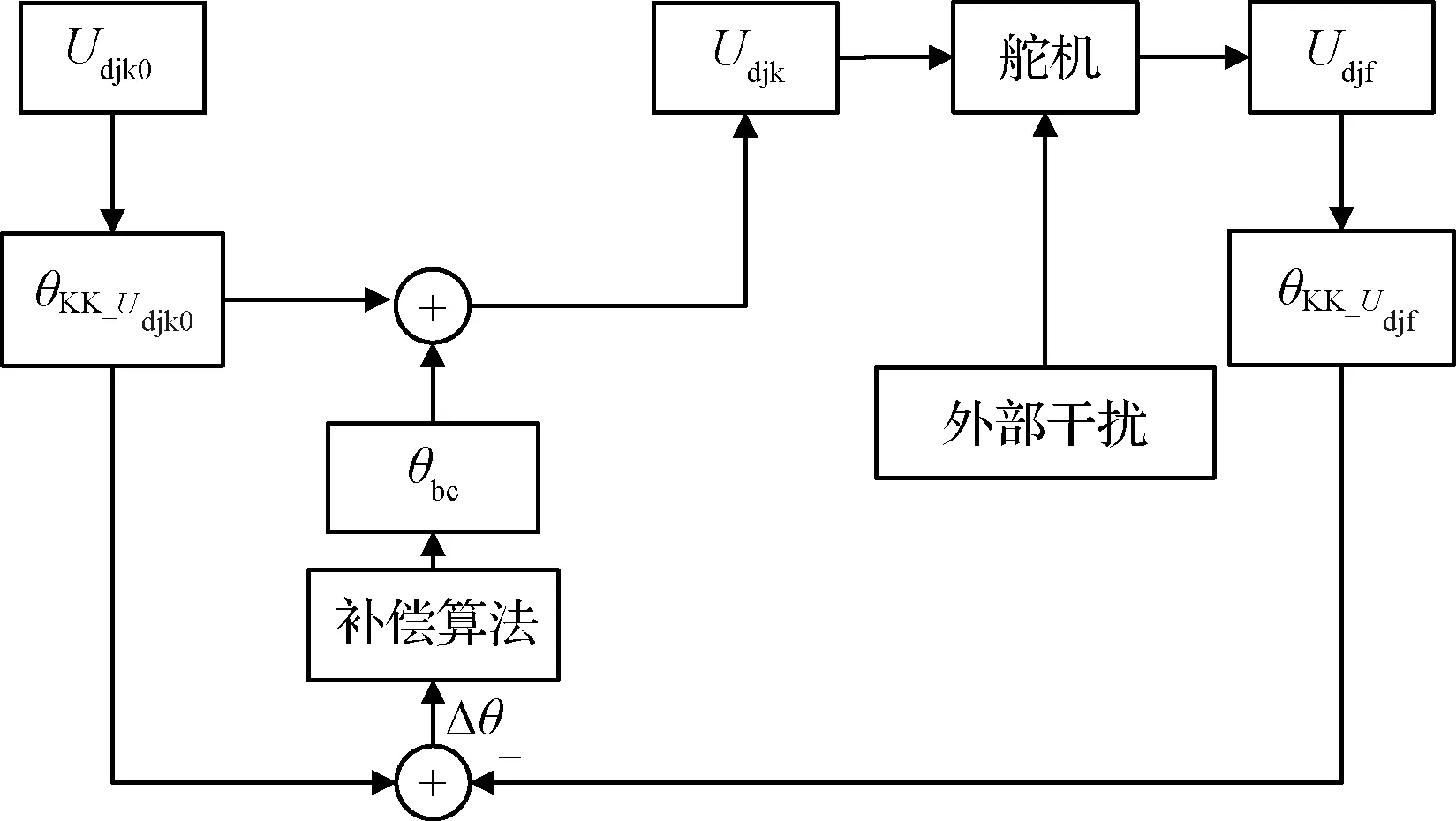
圖2 等效合力相位補償原理框圖Fig.2 Schematic diagram of phase compensation for equivalent force

圖3 等效合力幅值補償原理框圖Fig.3 Schematic diagram of amplitude compensation for equivalent force

根據圖2和圖3可知，實際算法實現過程中，需在每一個旋轉周期內計算一次輸入信號與輸出信號的等效合力之差，該偏差經過補償算法后，形成補償值并作用于舵系統的實際輸入，使得導彈飛行過程中的舵偏角的等效合力與制導控制系統指令的大小和方向保持一致。

設導彈期望的舵系統指令Udjk0為：

Udjk0(t)=U0sin(wDt+θ0)

(16)

則補償后實際的舵系統輸入指令為：

Udjk0(t)=(1+Kbc)U0sin(wDt+θ0+θbc)

(17)

3 數字仿真分析

3.1 仿真條件設置

通過數字仿真對比驗證補償算法的性能。設舵機標稱模型如下：

(18)

旋轉導彈舵系統帶寬通常要求在40Hz以上，因此將設置傳遞系數如下：

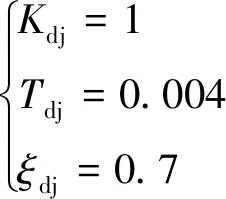
(19)

通過對式(19)中傳遞函數參數疊加隨機干擾模擬舵機不同控制指令及飛行負載等條件下表現出的非線性特性和外部擾動，隨機干擾服從正態分布，均值為0，標準差為參數值的50%。

飛行轉速條件：2 s以前轉速為3 r/s，在2～4 s時間內，轉速由3 r/s變化到12 r/s，之后保持12 r/s的飛行轉速。

為了便于對結果的直觀顯示，舵系統期望輸入指令的等效合力相位為0°，幅值為1。

在數字仿真中，基于以上的舵系統模型、負載和指令擾動及轉速變化條件，分別對比了固定值補償、轉速線性補償及本文提出的自適應補償方法的補償效果。

其中，固定值補償按照舵機標稱模型在10 Hz轉速條件下的滯后量進行補償。其補償值為20.6°。

根據式(12)可知，轉速線性補償應為：

Δθ=0.32wx(°)

(20)

在線自適應補償算法中的PI參數設置如下：

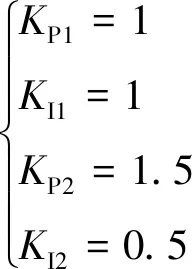
(21)

3.2 仿真結果分析

由于傳統的補償方法僅能對等效合力相位進行補償，幅值補償部分僅對自適應補償前和補償后的結果進行對比。仿真結果如圖4所示。

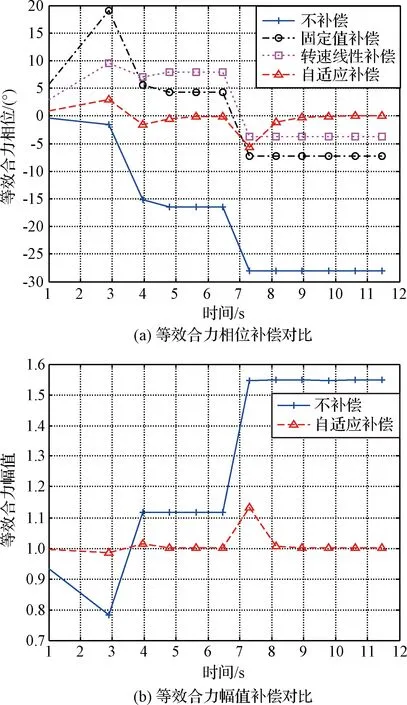
圖4 等效合力補償結果Fig.4 Compensation result of equivalent force

從圖4可知，在變轉速和不確定擾動條件下，固定值補償的效果最差，轉速線性補償能夠一定程度上彌補轉速對等效合力相位的影響，但在舵系統自身參數攝動條件下，補償精度易受影響，魯棒性和補償精度均較差。

本研究提出的自適應補償算法在動態過程中能夠實現較小的控制相位偏差和輸出幅值偏差，在參數攝動或轉速變化結束后，等效合力輸出約在10個彈旋周期內收斂到期望輸入的狀態，相比于傳統的補償方法，在相位控制上更加準確，魯棒性更強，同時彌補了傳統方法無法進行幅值補償的弊端。

4 結 論

研究提出的等效合力補償方案只需要實時在線計算舵系統輸入和輸出信號的等效合力幅值和相位，然后按照補償算法通過軟件實現補償，最終保證舵系統輸出的等效合力滿足預期要求。整個方案工程實現簡單、等效合力補償準確，且具有較強的魯棒性，對于提升旋轉導彈制導控制性能具有重要意義。另外，文中以正弦舵為例，通過理論分析和數字仿真檢驗了該補償算法的合理性及可行性，對于采用等幅不等寬氣動舵機的旋轉導彈，由于其等效合力機理相同，因而該算法同樣適用。