一種深空天文測角導航中的星歷誤差抑制方法
寧曉琳,晁 雯,楊雨青
(北京航空航天大學儀器科學與光電工程學院,北京 100191)
0 引 言
天文導航是一種全自主,誤差不隨時間積累的深空探測器導航技術[1]。天文導航方法按量測量的不同可分為測角導航[2]、測速導航[3]、測距導航[4]三種,其中,天文測角導航是通過觀測天體間的角度信息進行導航,目前已經成功應用于水手號[5],海盜號[6],伽利略號[7],深空1號[8],深度撞擊號[9]等深空探測器上。
目標天體的星歷誤差對天文測角導航的精度有很大的影響。以火星探測器為例,文獻[10]指出,在日心坐標系中,火星和火衛一的星歷誤差都會影響天文測角的導航精度。但在火星質心坐標系中,只有火衛一星歷誤差對導航精度有影響,而火星星歷誤差對導航精度的影響很小。在火星質心坐標系中,1 km的火衛一的星歷誤差會引起約4 km的位置誤差。文獻[11-12]指出,1950年火衛一的星歷誤差約為1 km,從1950年遞推至2050年會增加8 km。因此,如何抑制火星質心坐標系下火衛一星歷誤差對探測器導航精度的影響成為一個亟需解決的問題。
針對天文導航中星歷誤差的抑制問題,許多學者進行了深入的研究,也取得了很多研究成果。文獻[13]提出一種以時間差分脈沖到達時間(Time of arrival, TOA)作為量測量的脈沖星導航方法,該方法測量探測器相鄰時刻TOA的差值,以減小脈沖星星歷誤差等引起的系統偏差。文獻[14]提出一種差分X射線脈沖星輔助天文導航的方法,該方法利用探測器相鄰時刻的TOA差值和火衛一、火衛二及其背景恒星的星光角距作為量測量,有效抑制了脈沖星星歷誤差和星載時鐘誤差。文獻[15]提出一種X射線脈沖星/星光多普勒組合導航方法,以兩個探測器之間的TOA差值、相對位置以及在恒星方向上的相對速度關系為量測量,消除由脈沖星星歷誤差引起的系統誤差且不受太陽徑向固有運動的影響。以上所研究的都是采用時間差分方法抑制脈沖星導航中星歷誤差的影響。
綜上,提出一種基于星光角距/時間差分星光角距的深空探測器天文測角導航中的目標天體星歷誤差抑制方法。以火星探測器為例,分析了火衛一星歷誤差對導航精度的影響,建立了火衛一時間差分星光角距的量測模型。通過將火星星光角距和火衛一星光角距相結合,發揮了兩種量測的優勢。仿真結果表明該方法可以有效抑制火衛一的星歷誤差對導航結果的影響。同時,本文還對影響導航精度的導航恒星個數、火星敏感器精度、火衛一敏感器精度、星歷誤差的大小和濾波周期進行了分析。
1 天文測角導航的基本原理
深空探測器的天文測角導航是在探測器軌道動力學方程和天體間角度信息的基礎上,利用濾波技術估計探測器的位置和速度[16-17]。文中以火星探測器為例,給出了探測器天文測角導航的狀態模型和量測模型。
1.1 天文測角導航狀態模型
火星探測器的運動方程可以看作以火星為中心天體的二體模型,在火星質心坐標系下為:
(1)
式中:rmp和vmp是探測器相對火星的位置矢量和速度矢量;μm是火星的引力常數;w1是過程噪聲。
設狀態量為Xk=[rmpvmp]T,則火星質心坐標系下的狀態模型可以寫作:
Xk=f(Xk-1,T)
(2)
1.2 天文測角導航量測模型
以火星和火衛一及其背景恒星間的星光角距作為天文測角導航的量測量,其量測模型為:
(3)
式中:s1,s2表示火星質心坐標系下導航恒星的星光矢量;rpp是探測器相對火衛一的位置矢量;vθm,vθp是量測噪聲。
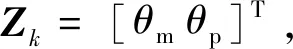
Zk=h1(Xk)+Vk
(4)
2 星光角距/時間差分星光角距的天文導航方法
首先分析了火衛一星歷誤差對天文測角導航的影響,通過對時間差分星光角距量測方程的推導,從理論上說明時間差分可以消除天文測角導航中星光角距中的火衛一星歷誤差,并給出了時間差分星光角距和星光角距/時間差分星光角距天文測角導航的量測模型。
2.1 火衛一星歷誤差對天文測角導航的影響
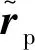
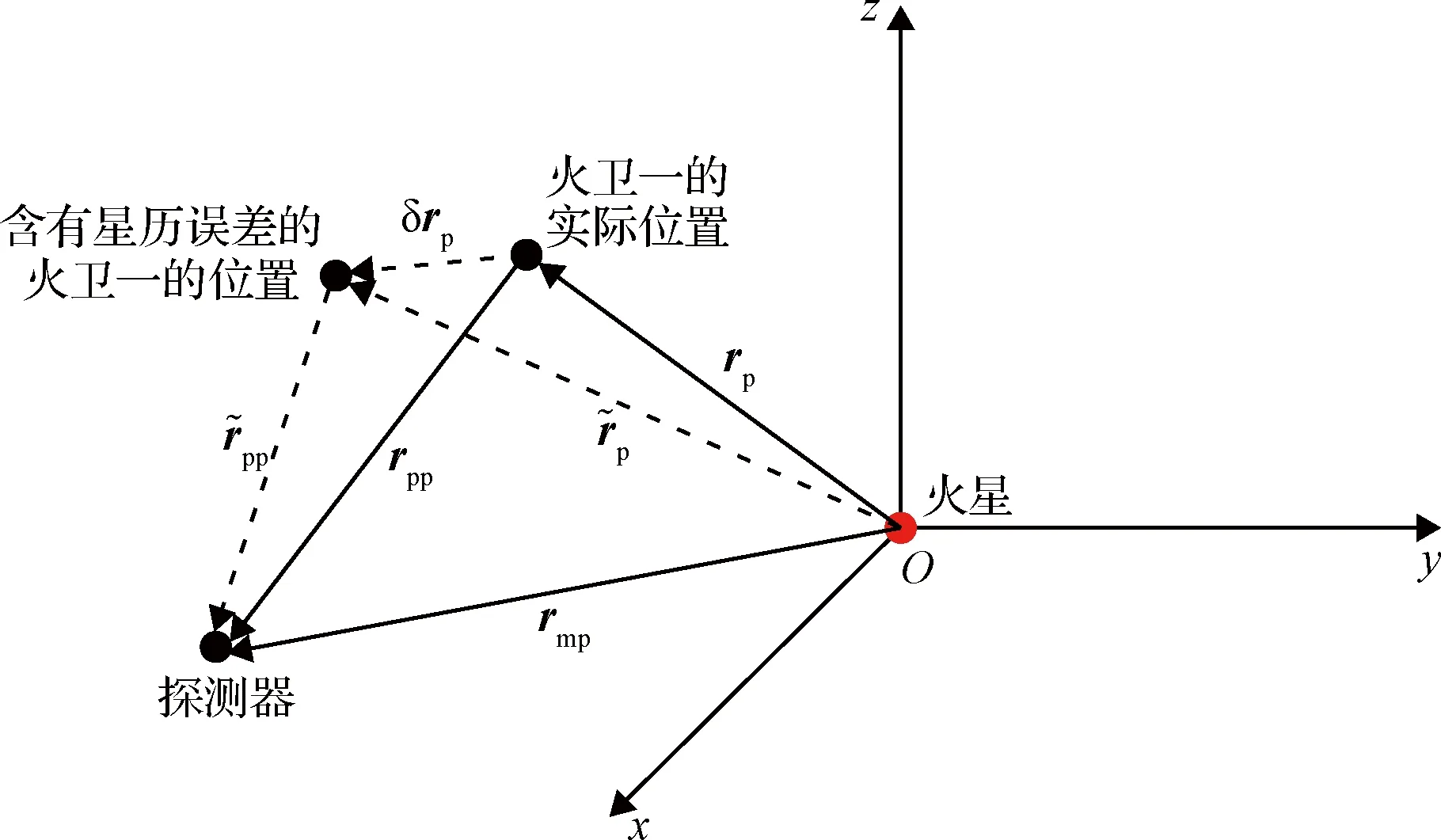
圖1 火衛一星歷誤差的影響Fig.1 The influence of Phobos ephemeris
(5)
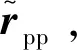
由式(3)和式(6)可知,火衛一星歷誤差引起的星光角距量測模型誤差Vθp為:
(7)
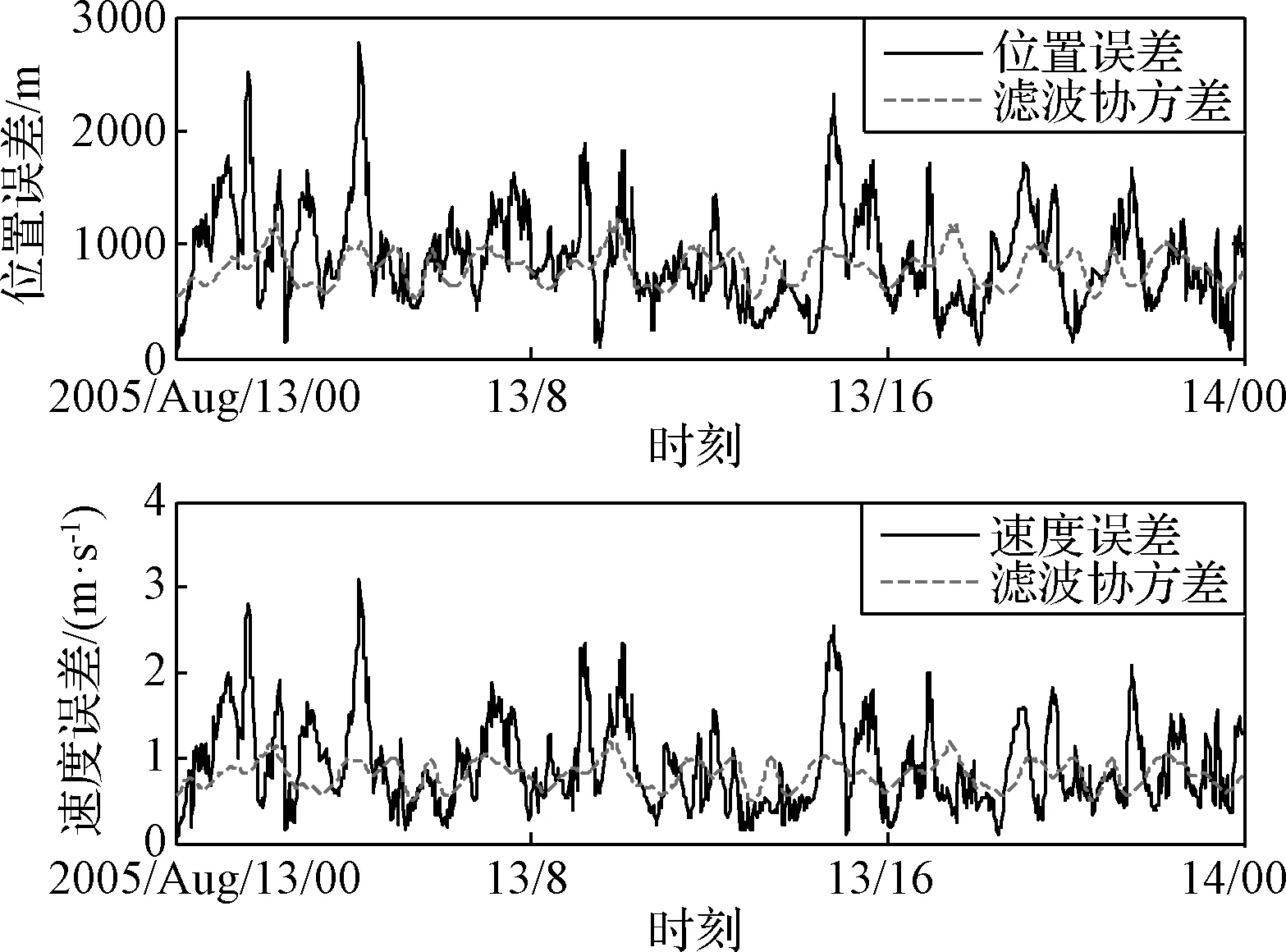
文獻[18]以MRO探測器為例,分析了由火衛一星歷誤差引起的量測模型誤差,發現Vθp為時變噪聲,且最大可達40″,說明火衛一星歷誤差對量測模型有很大的影響。
2.2 時間差分星光角距的量測模型
為了抑制火衛一星歷誤差的影響,對式(3)等式左右同時求余弦,則有:
(8)
當存在火衛一星歷誤差δrp時,火衛一星歷誤差引起的星光角距余弦的量測模型誤差為Vcθp,則有
(9)
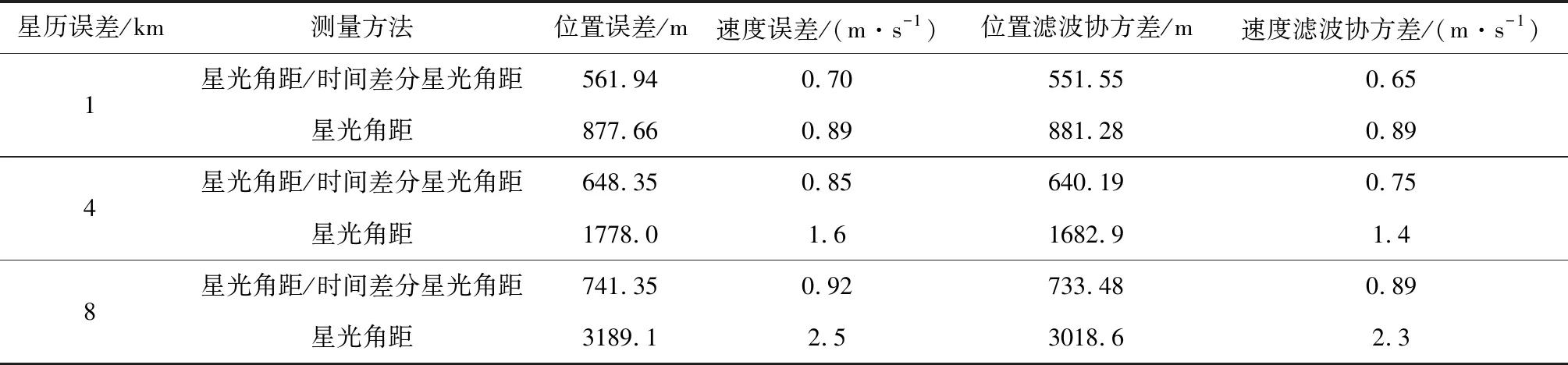
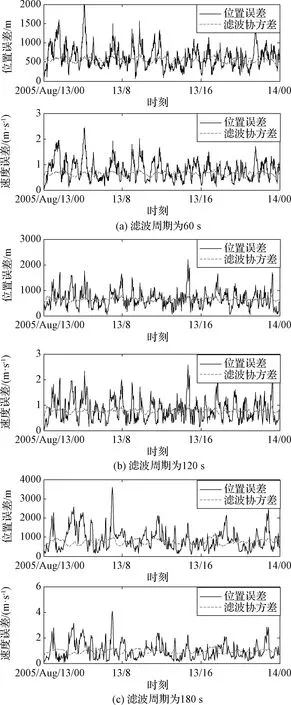
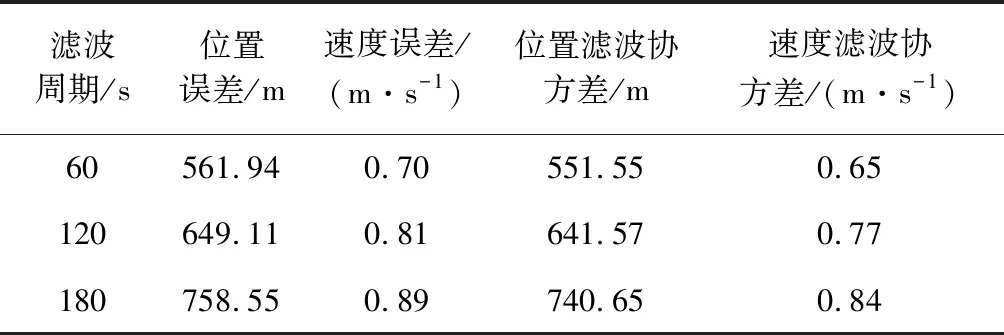
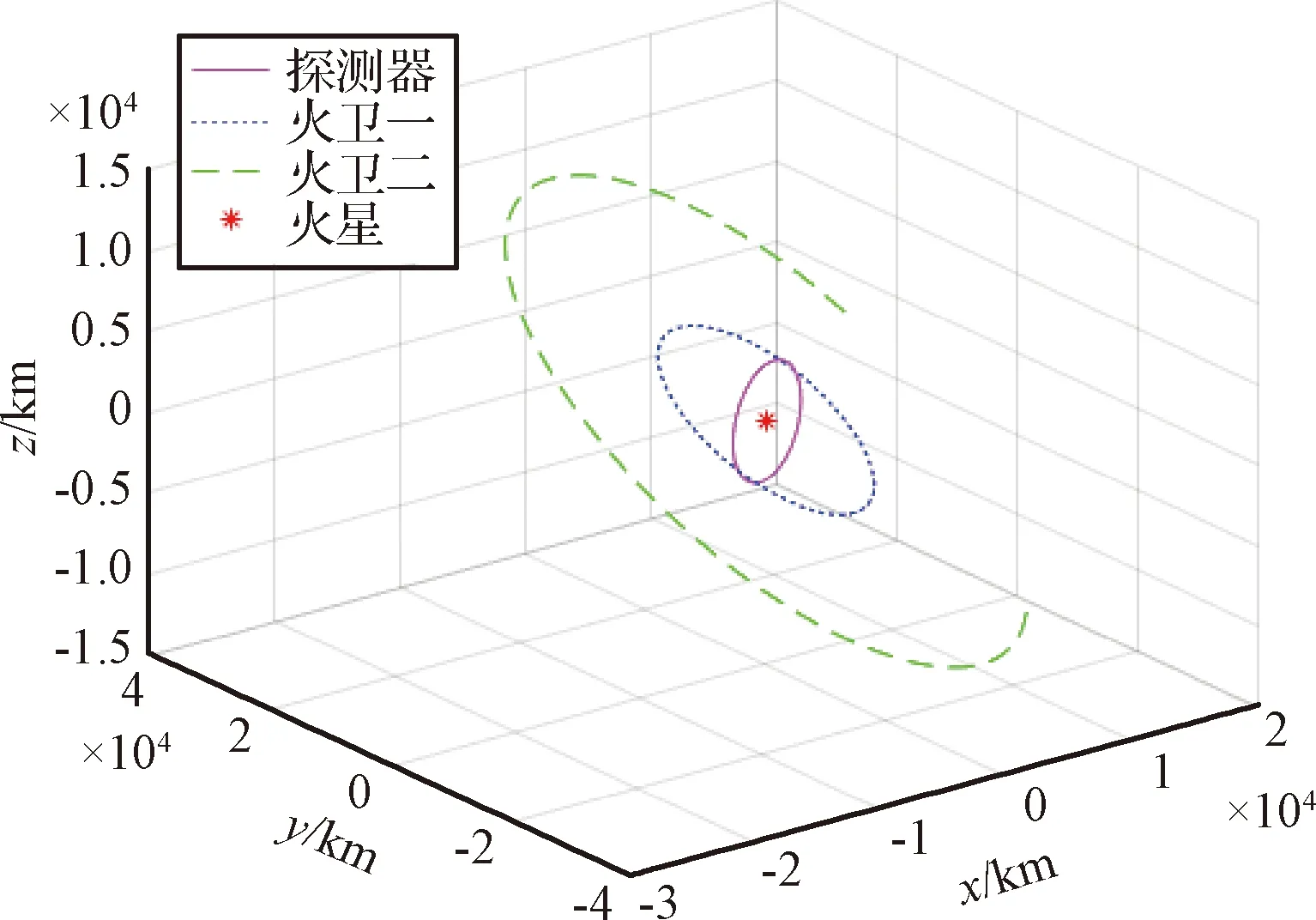
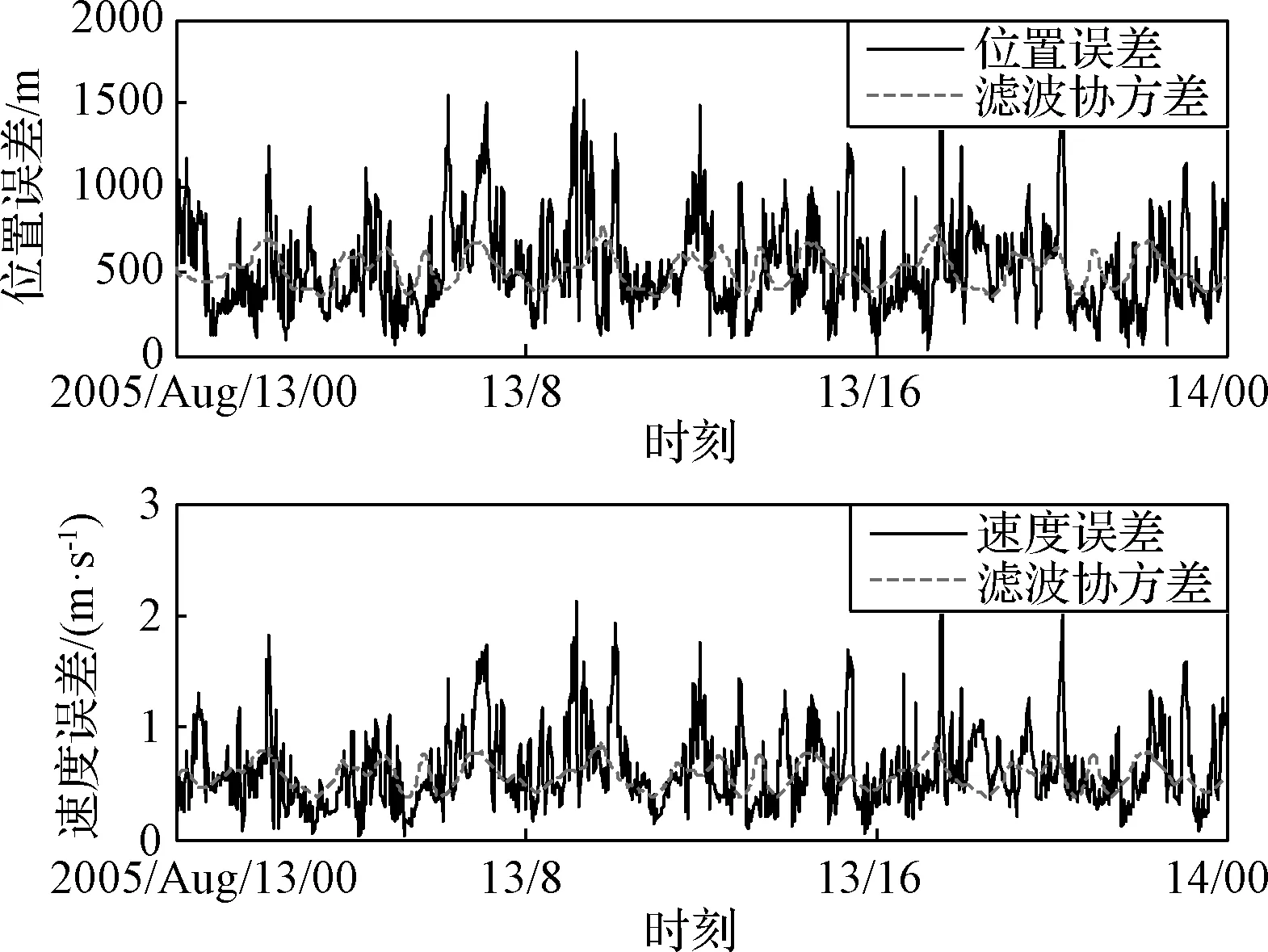
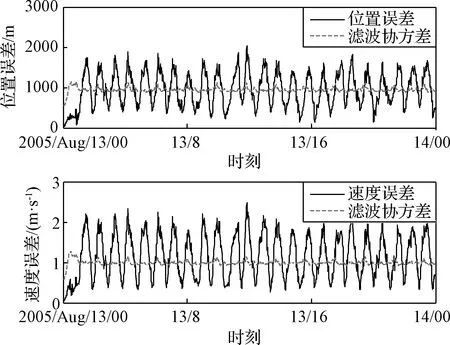
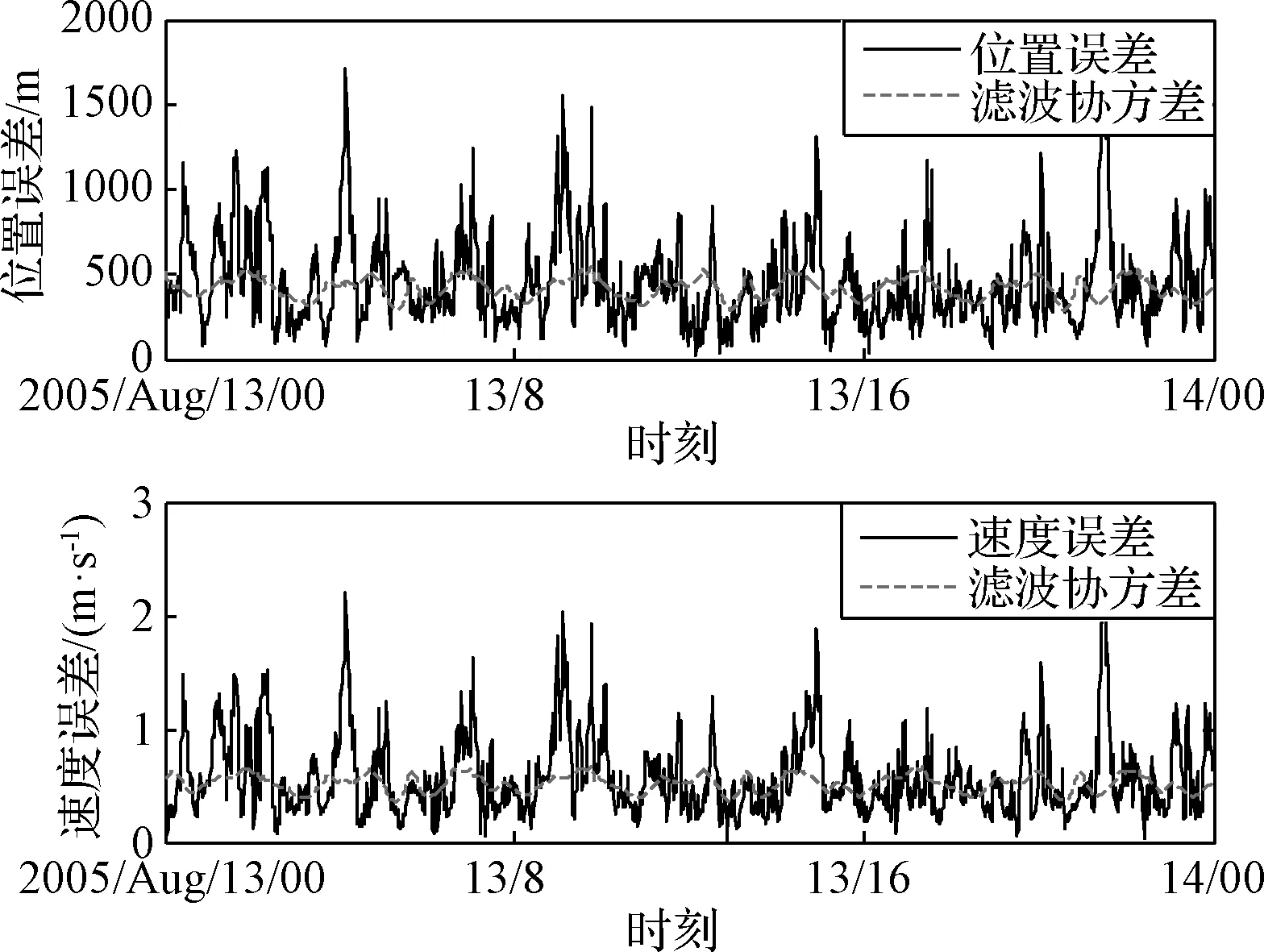
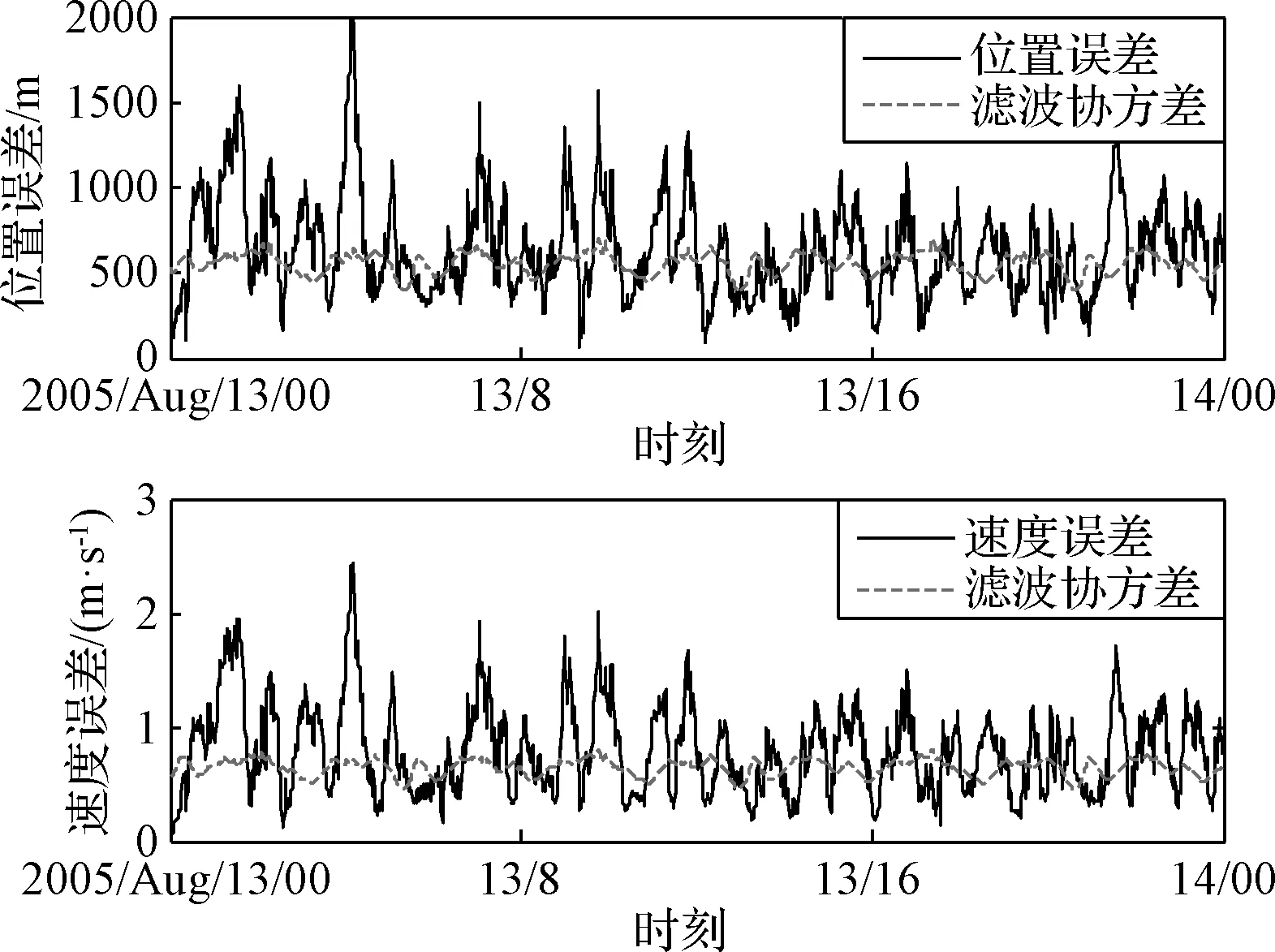
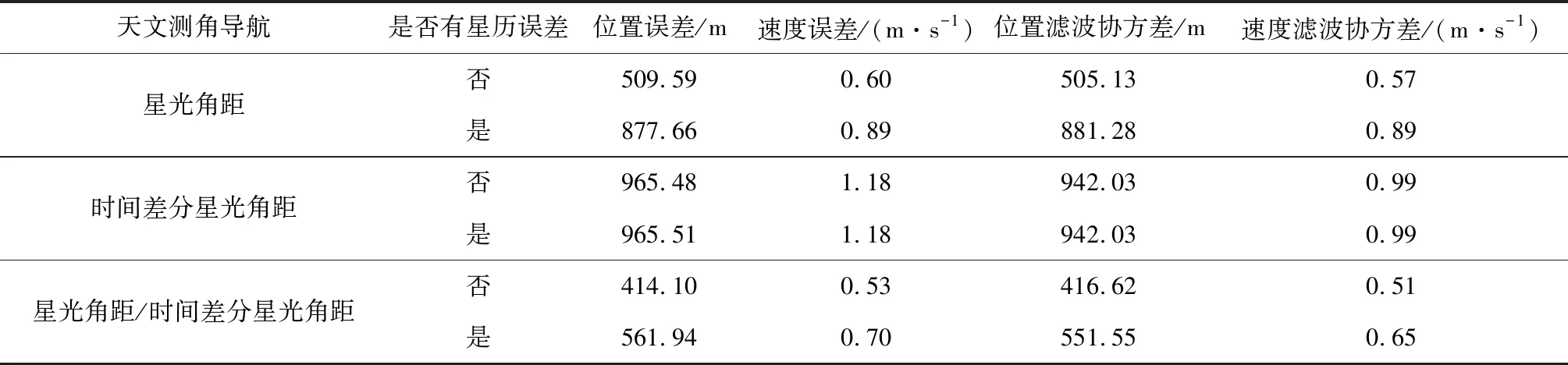
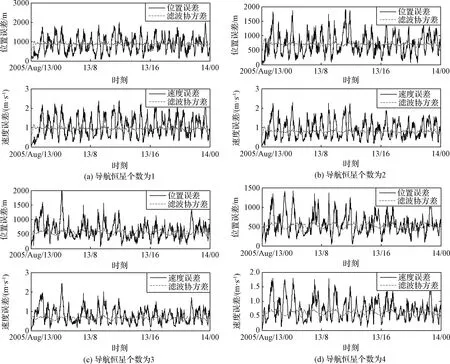
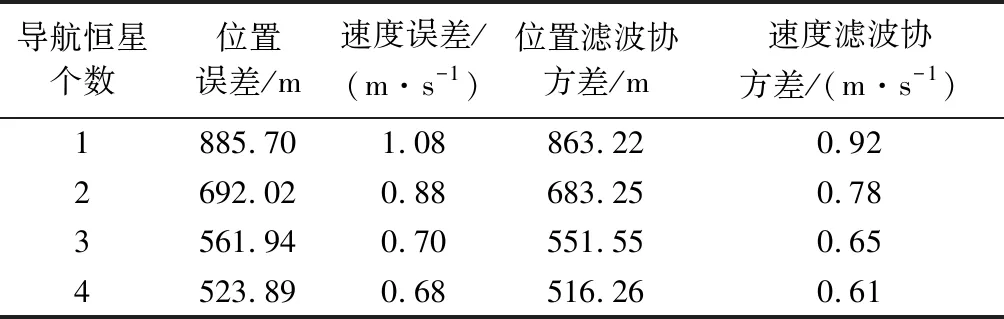
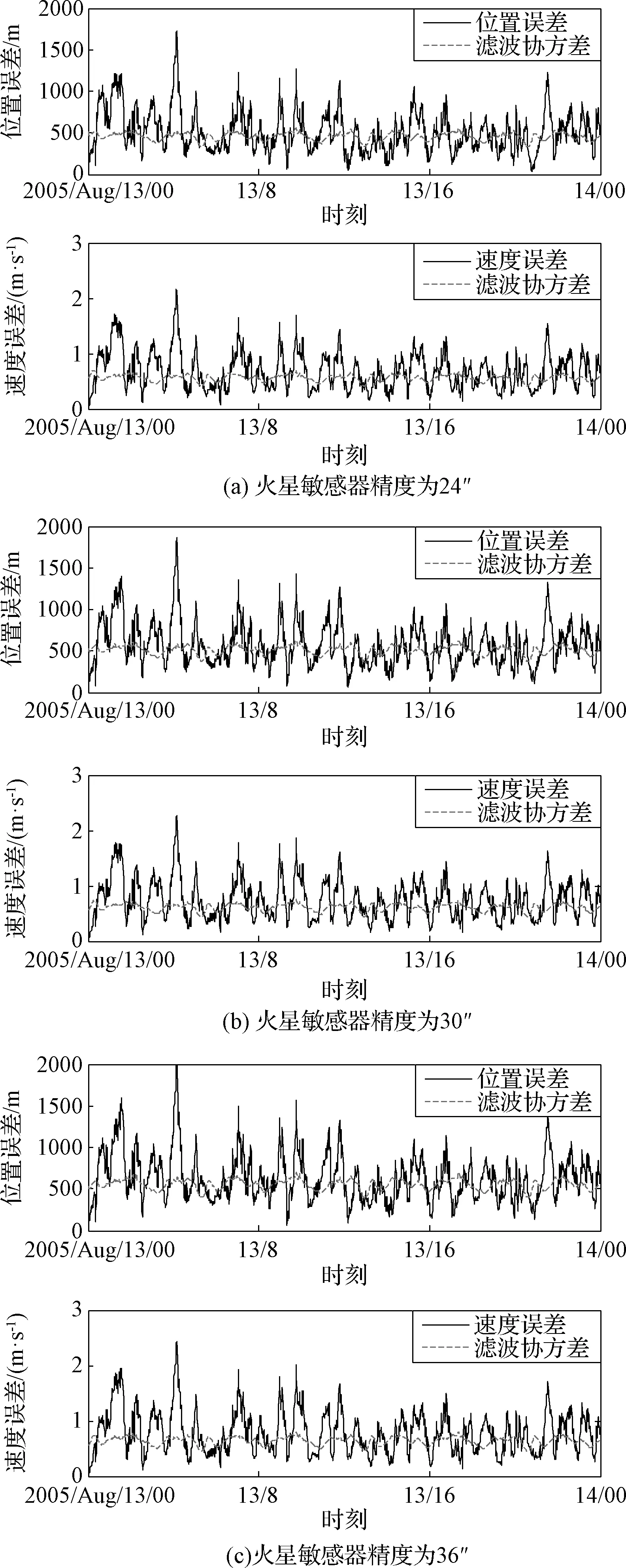
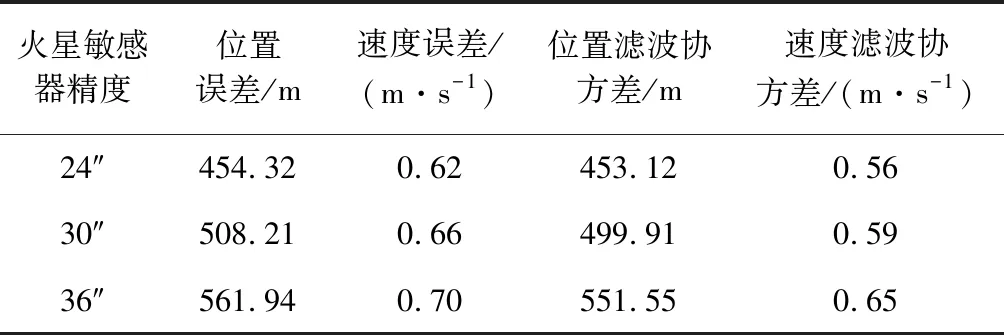
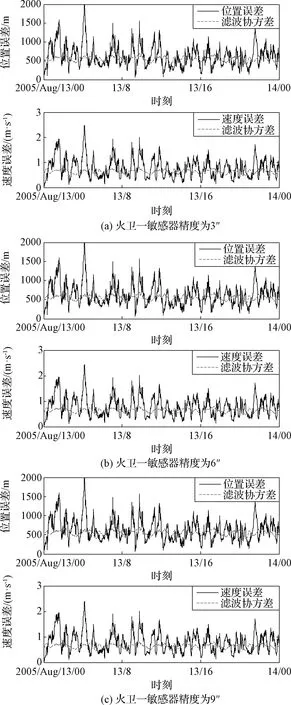
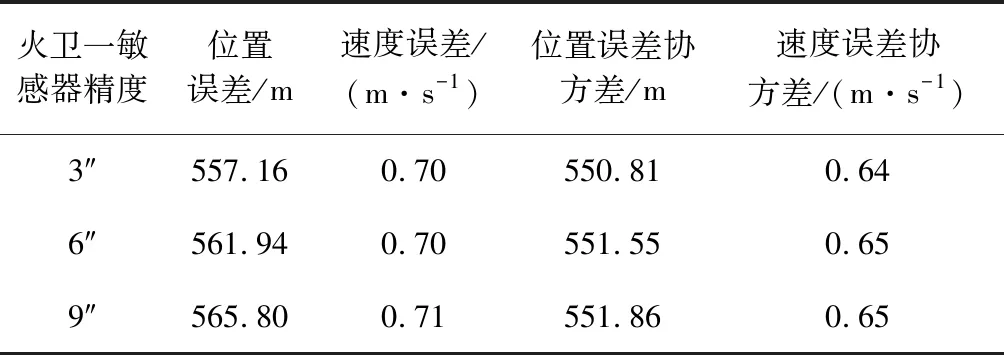
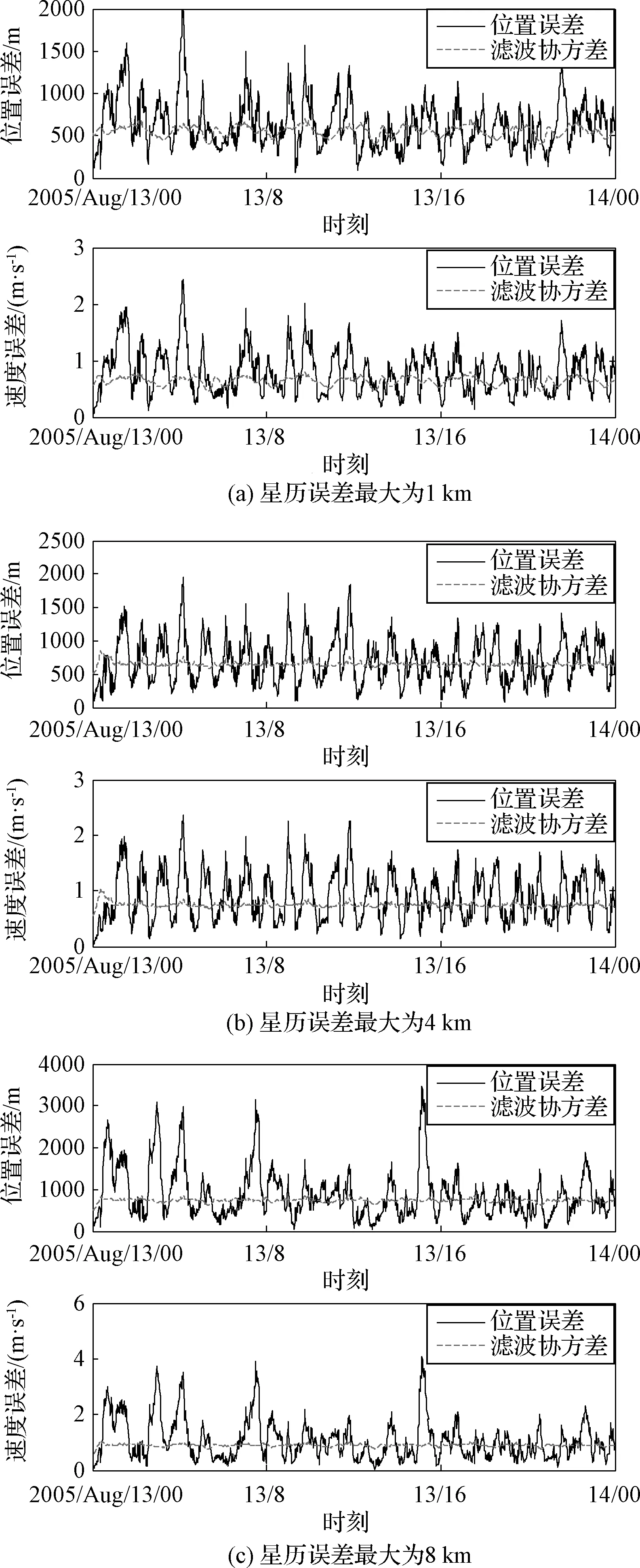
由于δrp< (10) 設基于時間差分星光角距的量測量為Δcθp(k),量測噪聲為Vcθ(k),則基于時間差分星光角距的天文測角導航量測方程可以寫作: Δcθp(k)=cos(θp(k))-cos(θp(k-1))= (11) 式中: Vcθ(k)=vp(k)-vp(k-1) (12) 當存在火衛一星歷誤差時,由式(6)、式(11)和式(12)得: vp(k)-vp(k-1)≈ vp(k)-vp(k-1)= vp(k)-vp(k-1) (13) 令δVcθp表示時間差分后的火衛一星歷誤差引起的量測模型誤差,則有: (14) 其中,由于δrp,rpp在短時間內(ΔT≤60 s)基本不變,s2不變。因此,時間差分星光角距可以抑制火衛一星歷誤差對量測模型的影響。 綜上所述,基于時間差分星光角距的天文測角導航量測方程可以表示為: vp(k)-vp(k-1)= h2(Xk)-h2(Xk-1)+Vcθ(k) (15) 時間差分星光角距導航方法存在以下兩點問題:(1)經過時間差分后的量測量不僅與當前時刻的狀態量還與上一時刻的狀態量相關,這與傳統卡爾曼濾波中k時刻的量測量只與當前時刻的狀態量一一對應的情況不同;(2)時間差分方法只能提供相對位置信息,絕對位置信息缺失。針對這兩個問題,本文采用一種根據狀態模型以當前時刻狀態量解算上一時刻狀態量的方法,并將火衛一的時間差分星光角距與火星星光角距一起作為量測量。量測方程可以寫作: (16) 若k時刻以星光角距為觀測量的量測誤差方差陣為Rk,則以星光角距余弦為觀測量時,其對應的量測誤差方差陣為 (17) 以時間差分星光角距余弦為觀測量時,其對應的量測誤差方差陣為 E(vp(k)vp(k)T-vp(k)vp(k-1)T- vp(k-1)vp(k)T+vp(k-1)vp(k-1)T) (18) 以2005年的MRO探測器的軌道為例進行仿真分析[19],圖2為MRO探測器在火星質心坐標系下的軌道圖。仿真數據由STK (System tool kit)產生。其半長軸為3709.5 km,軌道傾角為95°,軌道偏心率為0.113°。火星,火衛一及其背景恒星的星歷由DE421和Tycho星歷產生。仿真時間為2005年8月13日至2005年8月14日,坐標系采用J2000.0火星質心坐標系。仿真中所使用的火衛一的星歷誤差與參考文獻[18]相同,最大值為1 km。火星敏感器精度為0.01°,火衛一敏感器精度為6″,濾波周期為60 s。 圖2 MRO探測器的軌道Fig.2 The orbit of MRO 利用無跡卡爾曼濾波(UKF)方法對以星光角距、時間差分星光角距和星光角距/時間差分星光角距作為觀測量的天文測角導航方法進行了仿真分析和比較。其中,基于星光角距的天文測角導航的量測量為θm,θp,基于時間差分星光角距的天文測角導航的量測量為Δcθp,基于星光角距/時間差分星光角距的天文測角導航的量測量為θm,θp,Δcθp。 3.2.1三種天文測角導航方法的性能比較 1)基于星光角距的天文測角導航方法 圖3和圖4分別給出了沒有火衛一星歷誤差和有火衛一星歷誤差時的以星光角距作為量測量的天文測角導航的位置誤差和速度誤差。由圖3和圖4可知,當沒有火衛一的星歷誤差時,探測器的位置和速度的估計精度較高。當有火衛一的星歷誤差時,位置誤差和速度誤差明顯增大,位置誤差約為沒有星歷誤差的1.7倍。火衛一的星歷誤差對最終的導航精度有較大影響。 圖3 沒有星歷誤差時基于星光角距的天文測角導航結果Fig.3 Estimation error of celestial navigation using starlight angle without ephemeris error 圖4 有星歷誤差時基于星光角距的天文測角導航結果Fig.4 Estimation error of celestial navigation using starlight angle with ephemeris error 2)基于時間差分星光角距的天文測角導航方法 圖5給出了沒有火衛一星歷誤差和有星歷誤差的情況下時間差分天文測角的導航結果,由于二者結果基本一致,故省去對比圖。由于時間差分技術抑制了火衛一的星歷誤差,因此火衛一的星歷誤差對時間差分天文測角導航幾乎沒有影響。但從圖中可以看出誤差收斂性較差,且與圖3和圖4相比,精度較低,原因是時間差分星光角距只能提供相對位置信息,不能提供絕對位置信息,因此導航精度有限。 圖5 基于時間差分星光角距的天文測角導航結果Fig.5 Estimation error of celestial navigation using time differential starlight angle 3)基于星光角距/時間差分星光角距的天文測角導航方法 圖6和圖7給出了沒有火衛一星歷誤差和有火衛一星歷誤差時天文測角/時間差分天文測角的導航結果。由圖6和圖7可知,探測器的位置和速度都得到了較好的估計。但當有火衛一的星歷誤差時,位置誤差和速度誤差較大一些,約為沒有火衛一星歷誤差時的1.5倍。 圖6 沒有星歷誤差時基于星光角距/時間差分星光角距的天文測角導航結果Fig.6 Estimation error of celestial navigation using starlight angle/time differential starlight angle without ephemeris error 圖7 有星歷誤差時基于星光角距/時間差分星光角距的天文測角導航結果Fig.7 Estimation error of celestial navigation using starlight angle/time differential starlight angle with ephemeris error 表1給出了三種方法在8組不同的量測噪聲下濾波收斂后的蒙特卡羅仿真平均結果。仿真結果的統計時間段為2005年8月13日12:00至2005年8月14日00:00。由表1可知,當有星歷誤差時,基于星光角距/時間差分星光角距的天文測角導航方法的位置誤差是傳統天文測角導航方法的64%,是時間差分星光角距導航方法的58%。說明新方法可有效抑制火衛一星歷誤差的影響。 表1 火衛一星歷誤差對天文測角導航方法精度影響結果Table 1 The results of ephemeris error of Phobos on the accuracy of the celestial navigation 3.2.2影響因素分析 本節對有火衛一星歷誤差時基于星光角距/時間差分星光角距的天文測角導航方法的影響因素,包括導航恒星個數、火星敏感器精度、火衛一敏感器精度、星歷誤差大小和濾波周期分別進行了分析。 1)導航恒星個數對導航結果的影響 圖8和表2給出了在3.1所述的仿真條件下,導航恒星個數為1,2,3,4時在8組不同的量測噪聲下濾波收斂后的蒙特卡羅仿真平均結果。由圖8和表2可知,導航恒星個數小于等于3時,觀測恒星個數越多,導航精度越高。但當恒星個數大于3個時,增加導航恒星個數,位置速度濾波協方差降低緩慢,對導航精度提高有限。 圖8 導航恒星個數對基于星光角距/時間差分星光角距的天文測角的影響Fig.8 Impact of star number 表2 導航恒星個數對導航結果的影響Table 2 Estimation error of using different star number 2)火星敏感器精度對導航結果的影響 圖9給出了在3.1所述的仿真條件下,只改變火星敏感器精度時的導航結果。表3統計了火星敏感器精度分別為24″,30″,36″時在8組不同的量測噪聲下濾波收斂后的蒙特卡羅仿真平均結果。由圖9和表3可知,火星敏感器精度對導航結果有一定影響,敏感器精度越高,導航精度越高。火星敏感器精度每增加6″,位置誤差降低約50 m,位置速度誤差協方差近似線性減小。 3)火衛一敏感器精度對導航結果的影響 圖10給出了在3.1所述的仿真條件下,只改變火衛一敏感器精度時的導航結果。表4統計了火衛一敏感器精度分別為3″,6″,9″時在8組不同的量測噪聲下濾波收斂后的蒙特卡羅仿真平均結果。由圖10和表4可知,火衛一敏感器精度對導航結果影響較小。隨著敏感器精度的提高,導航性能僅有微小提升,位置速度誤差協方差幾乎不變。 圖9 火星敏感器精度對基于星光角距/時間差分星光角距的天文測角的影響Fig.9 Impact of Mars sensor accuracy 表3 火星敏感器精度對導航結果的影響Table 3 Estimation error of using different accuracy of Mars sensor 圖10 火衛一敏感器精度對基于星光角距/時間差分星光角距的天文測角的影響Fig.10 Impact of Phobos sensor accuracy 表4 火衛一敏感器精度對導航結果的影響 圖11 星歷誤差大小對基于星光角距/時間差分星光角距的天文測角的影響Fig.11 Impact of ephemeris error magnitude 4)星歷誤差大小對導航結果的影響 圖11給出了在第3.1節所述的仿真條件下,只改變星歷誤差大小時的導航結果。表5統計了星歷誤差最大值為1 km,4 km,8 km時,新方法與傳統天文測角導航方法在8組不同的量測噪聲下濾波收斂后的蒙特卡羅仿真平均結果的對比。由圖11和表5可知,星歷誤差大小對導航結果有較大影響。星歷誤差越大,導航精度越低,位置速度誤差協方差近似線性增大,但相對傳統基于星光角距的天文測角導航方法,新方法仍有較好的估計效果。 5)濾波周期對導航結果的影響 圖12給出了在第3.1節所述的仿真條件下,只改變濾波周期時的導航結果。表6統計了濾波周期分別為60 s,120 s,180 s時在8組不同的量測噪聲下濾波收斂后的蒙特卡羅仿真平均結果。由圖12和表6可知,系統受濾波周期影響較明顯,濾波周期越長導航精度越差,且位置速度濾波協方差近似線性增大。這是因為雖然濾波周期增大,時間差分引起的量測噪聲影響減小,但濾波周期越長,系統狀態模型的線性化誤差越大,導致系統導航精度降低。 本文主要介紹了基于星光角距/時間差分星光角距的天文測角導航方法。首先建立了基于星光角距的天文測角導航的狀態模型和量測模型,通過火衛一星歷誤差對天文測角導航精度的影響分析,表明火衛一星歷誤差對天文測角導航結果影響很大且可以通過時間差分技術抑制。然后,推導了時間差分星光角距量測方程,從理論上說明時間差分可以消除天文測角導航中星歷誤差。最后,建立了火衛一的時間差分星光角距的量測模型,并將其與火星星光角距一起作為量測量,實現了對火衛一星歷誤差的抑制。研究利用MRO探測器對基于星光角距/時間差分星光角距的天文測角導航方法進行了仿真校驗,仿真結果表明基于星光角距/時間差分星光角距的方法可以有效抑制火衛一的星歷誤差,提高導航精度。除火星探測任務外,該方法還可應用于其它深空探測任務中。 表5 星歷誤差大小對導航結果的影響Table 5 Estimation error of using different magnitude of ephemeris error 圖12 濾波周期對基于星光角距/時間差分星光角距的天文測角的影響Fig.12 Impact of filter period 表6 濾波周期對導航結果的影響Table 6 Estimation error of using different filter period2.3 星光角距/時間差分星光角距的量測模型及噪聲方差陣
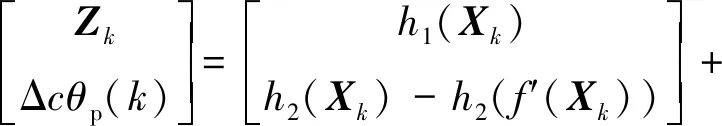
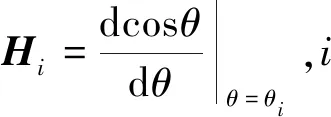
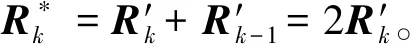
3 仿真校驗與分析
3.1 仿真條件
3.2 仿真結果
4 結 論