分數除法計算中的探究工具

駱良豪

【摘要】分數除法是小學數學計算學習中一個重要的組成部分.《義務教育數學課程標準（2011年版）解讀》指出，不僅會根據法則、公式等正確地進行運算，而且理解運算的算理，能夠根據題目條件尋求正確的運算途徑，稱為運算能力.只有理解了運算算理的運算能力才是真正具有生產性的.

【關鍵詞】算理;工具;策略

“分數除以整數”是“分數除法”這一單元的起始課，是學生在掌握了分數乘法以及倒數知識的基礎上學習的知識.分數除法不僅與分數乘法的意義、計算及其應用有著密切聯系，而且還和商不變的性質有聯系.

對于“分數除以整數”一課的教學，大部分教師都感到很困難，困難的并不是計算的算法，而是讓學生理解計算的算理.很多時候因為學生不理解算理，最終導致算法錯誤，因此大部分教師的解決辦法只是讓學生死記硬背，但這樣顯然沒有達到課程標準提出的要求.學生在進行分數除法的運算時，還是經常會出現把被除數的分子和分母顛倒再和除數相乘的錯誤，而且這樣的錯誤很普遍，這說明學生沒有理解分數除法的運算算理.只有理解了算理，學生在算法上才不容易出錯.

既然在學習分數除法的過程中學生有那么大的困難，那么學生是否可以進行自主探究呢？學生自己參與課堂，自己探究，是不是可以更好地理解算理呢？他們需要什么樣的探究工具來實現有意義的學習？

計算分數除以整數的一種思考方式是與分數乘法進行類比推理，即分子除以分子，分母除以分母;另一種思考方式是利用平均分和分數乘法的意義，把“除以一個整數”轉化為“乘這個數的倒數”.當然，不論哪種方法都是利用以前學過的知識來解決分數除以整數這個問題，因此“平均分和分數乘法的意義”是學生探究分數除以整數不可或缺的工具.

另外，六年級學生的思維已經開始從具象思維向抽象思維轉變，代數思維逐步形成.學生除了可以畫圖驗證，并聯系平均分與分數乘法之外，也可用“商不變的性質”來轉化，這可以讓學生理解數學其實就是利用舊知識來解決新問題，并且可讓學生在推導的過程中理解“除以一個數等于乘這個數的倒數”，掌握分數除以整數的計算方法.“分數除以整數”的學習也是為接下來學習“一個數除以分數”做鋪墊，是一節教結構的課，學生要在這節課的學習中學會分數除以整數的算理和算法，并把所學方法應用到下個課時的學習中.下面是筆者在上課時的部分教學片段：

一、片段教學

（一）借助情境，探究算理

教師借助情境，把一張紙的 4 5 平均分成2份，問：每份是這張紙的幾分之幾？列式： 4 5 ÷2= 2 5 .

師：請你們試著畫一畫，算一算.

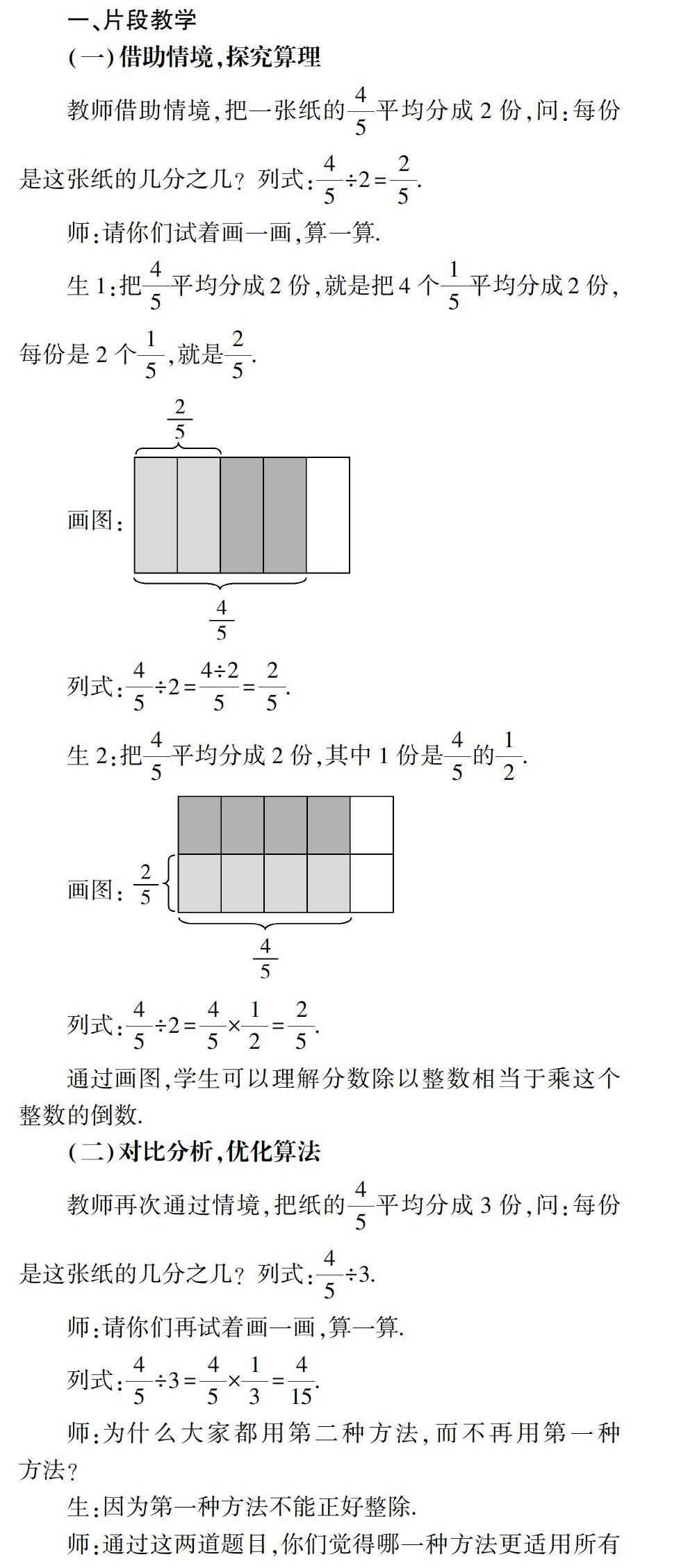
生1：把 4 5 平均分成2份，就是把4個 1 5 平均分成2份，每份是2個 1 5 ，就是 2 5 .

畫圖：

列式： 4 5 ÷2= 4÷2 5 = 2 5 .

生2：把 4 5 平均分成2份，其中1份是 4 5 的 1 2 .

畫圖：

列式： 4 5 ÷2= 4 5 × 1 2 = 2 5 .

通過畫圖，學生可以理解分數除以整數相當于乘這個整數的倒數.

（二）對比分析，優化算法

教師再次通過情境，把紙的 4 5 平均分成3份，問：每份是這張紙的幾分之幾？

列式： 4 5 ÷3.

師：請你們再試著畫一畫，算一算.

列式： 4 5 ÷3= 4 5 × 1 3 = 4 15 .

師：為什么大家都用第二種方法，而不再用第一種方法？

生：因為第一種方法不能正好整除.

師：通過這兩道題目，你們覺得哪一種方法更適用所有的分數除以整數？

生：第二種方法.

師：根據上面的兩個算式，請你們試著總結分數除以整數的算法，并用字母表示：

b[]a ÷c= b[]a × 1[]c

（三）驗證推理，揭示本質

師：是不是所有的分數除以整數都可以轉化成乘整數的倒數？請你們以 6 7 ÷4為例進行說明.

生1：用畫圖進行證明.

生2：說理解釋 6 7 ÷4相當求 6 7 的 1 4 .

師：數學都是用以前的知識來解決現在的問題，因此你們能不能用商不變的性質來解釋呢？同桌討論，并且動筆試一試.

生1：兩邊同時乘7.

師：大家認為哪種方法好，為什么？

生：第三種方法好，可以把除數變為1.

師：這樣的變式可以有無窮無盡個，我們可以用什么式子來表示？動手寫一寫.

二、教學策略

（一）動手畫圖，探究算理

在實際的情境中，學生動手畫圖，把自己的想法通過圖表達出來，這是最符合學生當前學情的方法.在小學階段，學生處于由具象思維向邏輯思維轉化的時期，大部分學生還沒有辦法憑借思考來理解算理，因此他們在畫圖的過程中可以感受到平均分和分數乘法的意義是一致的，同時體會到這是探究分數除以整數不可或缺的工具，并為接下來理解“除以一個數等于乘這個數的倒數”打下扎實的基礎.通過這種直觀的方式，學生可以更好地理解計算算理.

（二）對比概括，總結算法

分數除以整數有兩種計算方法：第一種方法是用分數的分子直接除以整數;第二種方法是用分數乘這個整數的倒數.但是在實際情境中，當“分子除以整數”無法整除時，學生會發現第一種方法雖然算得快，卻存在一定的限制，不適用所有分數除以整數，由此可以體會到第二種方法的普遍性.學生在對比的過程中體會不同方法的特征，從而會在不同的情況下用不同的方法，使自己的思維更靈活.

（三）驗證推理，理解本質

本節課最大的難點在于如何讓學生真正理解分數除以整數的算法.學生通過畫圖和對比，并結合平均分和分數乘法的意義發現了除以整數相當于乘它的倒數的計算方法.以前，教師講授到這一步也就結束了，接下來就是讓學生通過大量做題來鞏固知識，加深印象，但是這種教學方式的最大問題就是學生是通過記憶來計算的，雖然可能有些學生會理解算理和算法，但是他們經過一段時間之后就會忘記算理和算法，開始出現混亂.因此，在學生學會算法之后，教師還要讓學生學會對算法進行合情推理，使之適用于所有的分數除以整數，從而加深印象.學生的推理解釋一般都是通過前面所學的畫圖和算理進行說明的，但是這是不夠的，教師還要讓六年級的學生學會用邏輯思維進行轉化驗證，從而鍛煉他們的邏輯思維能力.教師要引導學生利用商不變的性質進行簡單證明.學生在轉化驗證的過程中，自己選擇合適的分數，并將分數除法中的除數變為1.在選擇的過程中，學生可以再一次體會算理.只要學生知道為什么要把除數變為1，他們就能更好地理解為什么除以一個數相當于乘這個數的倒數.教師還要給學生提出更高的要求，從而做好中小學銜接.

通過“分數除以整數”這節課，我們就可以發現，學生可以很容易發現并且掌握算法，而且按照以前的教學方法，我們都是直接教給學生算法，最多也就是應用畫圖和對比讓學生理解算理，使學生都用“分數除以整數相當于乘這個數的倒數”這個算法.但是通過這節課，我們不僅要讓學生在對比中發現規律，總結算法，還要讓學生經歷這個過程，發現規律，并且有意識地讓學生運用代數的方法總結算法，鍛煉學生的邏輯思維.而在這個過程中，“平均分和分數乘法的意義”是學生探究分數除以整數不可或缺的工具.在教學中，筆者要先了解學生的學情，因為六年級學生的思維還沒辦法完全抽象，所以要先讓學生畫圖，通過具體的圖，讓學生直觀地理解算理，接著利用“對比”來進一步幫助他們體會為什么除以整數相當于乘這個數的倒數.這節課我們的創新之處就在于讓學生自己運用商不變的性質，把分數除以整數轉化為分數乘這個數的倒數，并用字母進行表示.

學生通過本節課，先解決了分數的分子能夠被整數整除的特殊情況，再結合意義進行思考，寫出自己的想法，并借助畫圖進行理解;之后，教師引出分數的分子不能被整數整除的情況，讓學生體會哪一種方法更具有普遍性，感受分數除以整數可以利用分數的意義轉化為乘整數的倒數.教師再要求學生利用商不變的性質進行證明，并用字母證明普遍性，使學生在一步一步的教學中體會為什么除以整數就相當于乘這個整數的倒數.教師教給學生學習方法后，學生就學會了如何學習分數除法，也為接下來學習一個數除以分數打下基礎，有利于學生今后的學習.

【參考文獻】

[1]楊彩如.基于多元表征理論的小學分數除法計算教學研究[D].廣州：廣州大學，2019.

[2]葛敏輝.理解視域下“分數除法”計算教學認知起點的調查分析[J].小學數學教師，2018（3）：15，32-37.

[3]郝康英.例談小學分數除法的計算教學[J].教書育人，2014（15）：46-47.