帶精確時間延遲的兩臺機流水作業問題研究
王煥男
(三亞學院理工學院,海南 三亞 572022)
1 引言
關于帶精確時間延遲的兩臺機流水作業問題主要成果有:文獻[1](Ageev and Kononov,2006)對于問題F2| exactlj|Cmax設計1個3的近似算法,1.5-ε的難近似界,O(nlogn)時間內可解;對于問題F2|exactlj,aj≤bj|Cmax設計1個2的近似算法,1.5-ε的難近似界,O(nlogn)時間內可解;對于問題F2|exactlj,aj≥bj|Cmax設計1個2的近似算法,1.5-ε的難近似界,O(nlogn)時間內可解。文獻[1](Ageev and Kononov,2006)和[2](Ageev and Kononov,2007)對一般情況也設計了更好的近似算法,他們進一步證明了(1.5-ε)-近似算法的存在性,暗示P=NP。文獻 [2](Ageev and Baburin,2007)假設在單位加工時間下,證明了對于問題F2|exactlj,aj=bj= 1 |Cmax的近似因子是3/2,證明兩臺機的算法可以在O(n2logn)時間內實現。文獻[3](Yu,1996)證明這個問題是強NP-難的。文獻[4](Josh Glascock,Brian Hunter,2009)開發了基于遺傳算法(GA)和蟻群優化(ACO)的兩個元啟發式算法。文獻[5](Yumei Huo,HaibingLi,HairongZha,2009)研究帶確切延誤的兩臺機流水作業的排列排序,注意到甚至對于排列排序,這個問題仍然是強NP-難的,證明了對于一些特殊情況一些簡單的算法能用于找到最優排序。他們設計了第1個元啟發式算法,1個禁忌搜索算法和1個模擬退火算法解決這個問題。研究帶確切延誤的兩臺機流水作業的排列排序最小化總完工時間。對于一般情況,這個問題是NP-難的。研究多項式可解的特殊例子,對于一般情況開發了一些簡單啟發式算法和共通啟發式演算法。
對上述研究綜述進行匯總如表1所示。
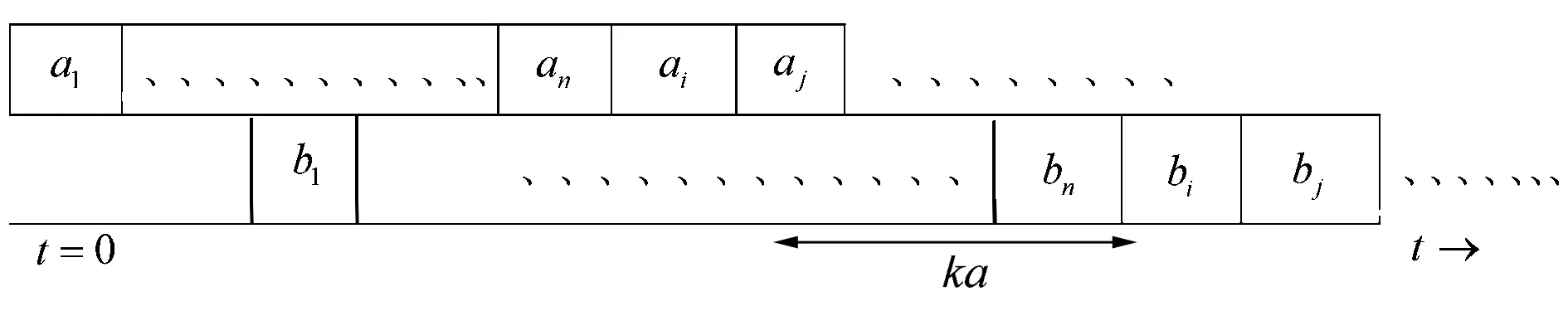
而本研究主要研究帶精確時間延遲的兩臺機流水作業問題。每個工件Jj(j=1,2,…,n)有兩道工序aj、bj,第一道工序先于第二道工序加工,第一道工序的完工時間caj與第二道工序的開始時間sbj之間存在一個精確時間延遲exactlj,即sbj=caj+lj。所有工序操作時間都相等aj=bj=a(j=1,2,…,n),且精確時間延遲是工序操作時間的整數倍lj=ka(k∈N+)。第一道工序在第一臺機器上執行,第二道工序在第二臺機器上執行,分別以極小化加權總完工時間,最大延誤時間和總延誤數為目標函數,設計了最優算法。

表1 帶精確時間延遲的兩臺機流水作業Tab.1 Flow operation of two machines with accurate time delay
上面問題用三參數分別表示為:F2|exactlj,aj=bj=a,lj=ka|∑wjCj,F2|exactlj,aj=bj=a,lj=ka|Lmax,F2|exactlj,aj=bj=a,lj=ka|∑Uj這3個問題。
2 F2|exact lj,aj=bj,lj=ka|∑wjCj的最優算法
本節主要研究帶精確時間延遲的兩臺機流水作業排序問題。每個工件記為Jj(aj,bj,lj,wj),目標函數為極小化加權總完工時間。分別考慮以下3種情況:
2.1 F2|exact lj,aj=bj=lj=a|∑wjCj的最優算法
當aj=bj=lj=a時,sb1=2a。因為每個工件的第一道工序aj在第一臺機器上執行,第二道工序bj在第二臺機器上執行,并且它們之間存在的是精確時間延遲,所以當第二道工序bj在第二臺機器上的開始時間sbj確定時,對應的第一道工序aj在第一臺機器的位置也唯一確定。因此只考慮每個工件的第二道工序bj,即此問題等價于1‖∑wjCj。考慮單臺機排序問題1‖∑wjCj,該問題存在多項式時間最優算法,Weighted Shortest Processing Time first (WSPT),即
LWF (Longest Weighted first):將所有工件重新排序,使得w1≥w2≥…≥wn,再按照J1,J2,…,Jn的順序加工工件。
定理2.1.1 LWF是問題F2|exactlj,aj=bj=lj=a|∑wjCj的最優算法,如圖1所示。
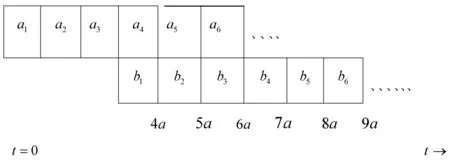
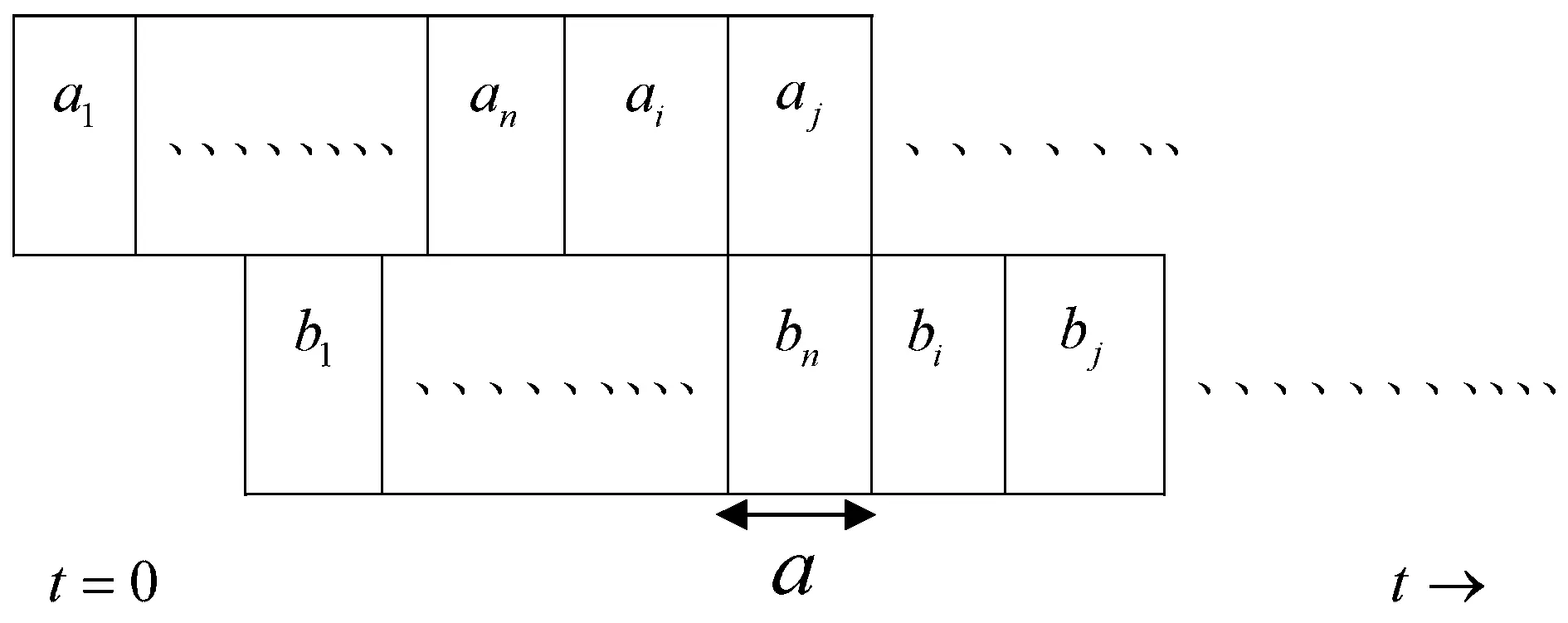
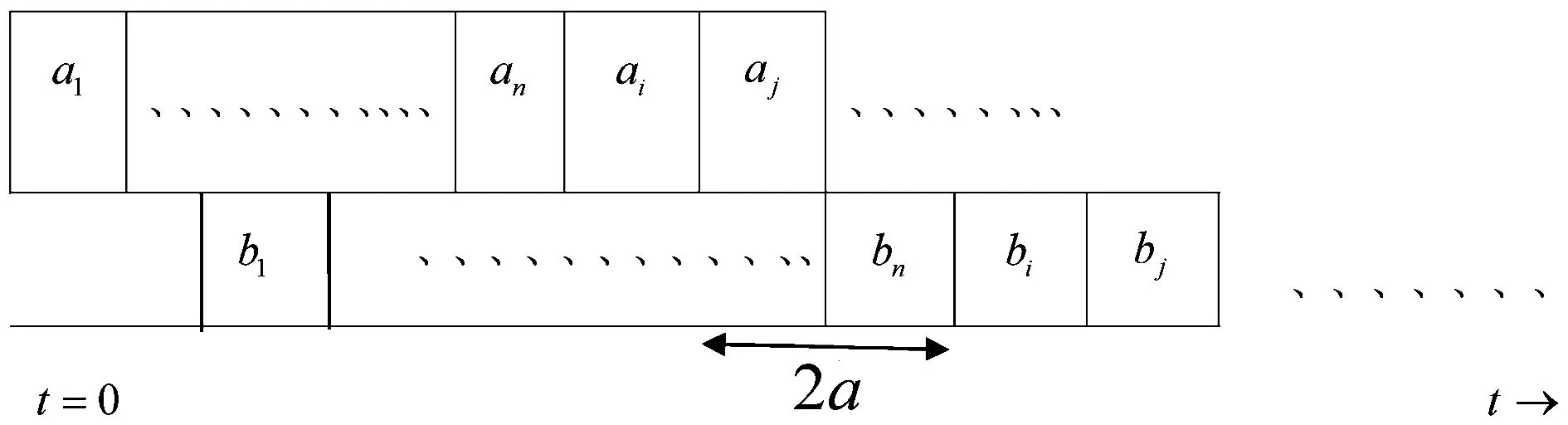
證明:用反證法。假設有一個最優排序,比如σ*,違反了LWF規則,則σ*中一定存在相鄰的兩個工件Ji和Jk,使得wi ∑wjCj(σ*)-∑wjCj(σ)=wi(sbi+bi)+wk(sbi+bi+bk)-wi(sbi+bi+bk)-wk(sbi+bk)=wkpi-wipk>0 即所得的排序σ目標值比最優值還要小,矛盾! 注:當wj=1時,問題變為1|exactlj,aj=bj=lj=a|∑Cj 圖1 最優排序Fig.1 Optimal sorting 當aj=bj=a,lj=2a時,sb1=3a。因為每個工件的第一道工序aj在第一臺機器上執行,第二道工序bj在第二臺機器上執行,并且它們之間存在的是精確時間延遲,所以當第二道工序bj在第二臺機器上的開始時間sbj確定時,對應的第一道工序aj在第一臺機器的位置也唯一確定。因此只考慮每個工件的第二道工序bj,即此問題等價于1‖∑wjCj。考慮單臺機排序問題1‖∑wjCj,該問題存在多項式時間最優算法,Weighted Shortest Processing Time first (WSPT),即 定理2.2.1 LWF是問題F2|exactlj,aj=bj=lj=2a|∑wjCj的最優算法,如圖2所示。 圖2 最優排序Fig.2 Optimal sorting 證明:用反證法。假設有一個最優排序,比如σ*,違反了LWF規則,則σ*中一定存在相鄰的兩個工件Ji和Jk,使得wi ∑wjCj(σ*)-∑wjCj(σ)=wi(sbi+bi)+wk(sbi+bi+bk)-wi(sbi+bi+bk)-wk(sbi+bk)=wkpi-wipk>0 即所得的排序σ目標值比最優值還要小,矛盾! J1,J2,…,Jn的順序加工工件。 注:當wj=1時,問題變為1|exactlj,aj=bj=a,lj=2a|∑Cj 定理2.3.1 LWF是問題F2|exactlj,aj=bj,lj=ka|∑wjCj的最優算法,如圖3所示。 圖3 最優排序Fig.3 Optimal sorting 證明:用反證法。假設有一個最優排序,比如σ*,違反了LWF規則,則σ*中一定存在相鄰的兩個工件Ji和Jk,使得wi ∑wjCj(σ*)-∑wjCj(σ)=wi(sbi+bi)+wk(sbi+bi+bk)-wi(sbi+bi+bk)-wk(sbi+bk)=wkpi-wipk>0 即所得的排序σ目標值比最優值還要小,矛盾! J1,J2,…,Jn的順序加工工件。 注:當wj=1時,問題變為1|exactlj,aj=bj=a,lj=ka|∑Cj 本節主要研究帶確切延誤的兩臺機流水作業排序問題。每個工件記為Jj(aj,bj,lj,dj),目標函數為極小化最大延誤。分別考慮以下3種情況: 當aj=bj=lj=a時,sb1=2a。因為每個工件的第一道工序aj在第一臺機器上執行,第二道工序bj在第二臺機器上執行,并且它們之間存在的是精確時間延遲,所以當第二道工序bj在第二臺機器上的開始時間sbj確定時,對應的第一道工序aj在第一臺機器的位置也唯一確定。因此只考慮每個工件的第二道工序bj,即此問題等價于1‖Lmax。單臺機最大延誤問題1‖Lmax也可以找到多項式時間算法,Earliest Due Date first (EDD),且是最優算法。 EDD:將工件重新排序使得d1≤d2≤…≤dn,再按照J1,J2,…,Jn順序加工。 定理3.1.1 EDD規則可以得到問題F2|exactlj,aj=bj=lj=a|Lmax的最優排序。 當aj=bj=a,lj=2a時,sb1=3a。因為每個工件的第一道工序aj在第一臺機器上執行,第二道工序bj在第二臺機器上執行,并且它們之間存在的是精確時間延遲,所以當第二道工序bj在第二臺機器上的開始時間sbj確定時,對應的第一道工序aj在第一臺機器的位置也唯一確定。因此只考慮每個工件的第二道工序bj,即此問題等價于1‖Lmax。單臺機最大延誤問題1‖Lmax也可以找到多項式時間算法,Earliest Due Date first (EDD),且是最優算法。 定理3.2.1 EDD規則可以得到問題F2|exactlj,aj=bj,lj=2a|Lmax的最優排序。 當aj=bj=a,lj=ka時,sb1=(k+1)a。因為每個工件的第一道工序aj在第一臺機器上執行,第二道工序bj在第二臺機器上執行,并且它們之間存在的是精確時間延遲,所以當第二道工序bj在第二臺機器上的開始時間sbj確定時,對應的第一道工序aj在第一臺機器的位置也唯一確定。因此只考慮每個工件的第二道工序bj,即此問題等價于1‖Lmax。單臺機最大延誤問題1‖Lmax也可以找到多項式時間算法,Earliest Due Date first (EDD),且是最優算法. 定理3.3.1 EDD規則可以得到問題F2|exactlj,aj=bj,lj=ka|Lmax的最優排序。 本節主要研究帶精確時間延遲的兩臺機流水作業排序問題,每個工件記為Jj(aj,bj,lj,dj),目標函數為極小化總延誤數。分別考慮以下3種情況: 當aj=bj=lj=a時,sb1=2a。因為每個工件的第一道工序aj在第一臺機器上執行,第二道工序bj在第二臺機器上執行,并且它們之間存在的是精確時間延遲,所以當第二道工序bj在第二臺機器上的開始時間sbj確定時,對應的第一道工序aj在第一臺機器的位置也唯一確定。因此只考慮每個工件的第二道工序bj,即此問題等價于1‖∑Uj。對于極小化誤工工件數的問題1‖∑Uj,1968年Moore給出了一個多項式時間的最優算法。 算法H: ①將工件按照EDD規則排序; ②計算當前排序中各工件的完工時間,如果已無延誤,則轉④,否則轉③; ③找出第1個延誤的工件,比如是第i個工件,則將其刪除,得到一個部分排序,返回②; ④將刪除的工件以任意順序排到最后,所得部分排序之后,輸出所得排序。 定理4.1.1 算法H可以得到問題F2|exactlj,aj=bj=lj=a|Lmax的最優排序如圖4所示。 圖4 最優排序Fig.4 Optimal sorting 證明:不妨d1≤d2≤…≤dn,設P=(S,F)為算法所得的排序,其中S為按期完工工件集,F為誤工工件集,即算法在第③步中刪除的工件集合。不妨設F≠Φ,令工件k是算法第1次執行到第③步時找到的延誤工件,于是i就是算法刪除的第1個工件。由算法規則可知 1,…,i-1沒有誤工工件,下面首先證明:存在最優排序P′=(S′,F′)(S′和F′定義同上),使得i∈F′。 設P′=(S′,F′)是一個最優排序且i∈S′。并記F′=π(r+1)…π(n),S′=π(1)…π(r),不妨認為dπ(1)≤dπ(2)≤…≤dπ(r)。再由于d1≤d2≤…≤dn,所以一定存在m使得: i∈{π(1),…,π(m)}?{1,…,i},{π(m+1),…,π(r)}?{i+1,…,n}。 并且由i定義,序列1,…,i產生延誤,因而{π(1),…,π(m)}≠{1,…,i}。于是存在1≤h≤i,h?{π(1),…,π(m)},所以有: {π(1),…,π(m)}∪{h}{i}?{1,…,k}{i}。 由此可知:{π(1),…,π(m)}∪{h}{i}按照EDD排列后不產生延誤,且這些工件的總加工時間比{π(1),…,π(m)}中工件總加工時間減少了,這表明在上述工件序列之后加上原來的π(m+1),…,π(r)也不產生誤工工件。換句話說,我們構造出了一個誤工工件數與P′相同但i是誤工工件的排序,即得到了滿足要求的最優排序。 根據上面這個結論,對工件數目作歸納,證明定理結論:顯然,當n=1時,該算法可以得到最優排序。假設算法對工件數為n-1的實例均能找到最優排序,則對任一工件數為n的實例,設P=(S,F)是算法所得的排序,工件i∈F如上定義。所以存在一個最優排序P′=(S′,F′),使得i∈F′,顯然有|S|≤|S′|。另一方面,考慮實例{1,…,i-1,i+1,…,n},由歸納假設及算法規則,算法得到的排序形如P=(S,F{i})且是一個最優排序。再注意到P′=(S′,F′{i})是該實例的可行排序,所以又可得到|S|≥|S′|。因此|S|=|S′|,算法對n個工件的實例也得到最優排序。 當aj=bj=a,lj=2a時,sb1=3a。因為每個工件的第一道工序aj在第一臺機器上執行,第二道工序bj在第二臺機器上執行,并且它們之間存在的是精確時間延遲,所以當第二道工序bj在第二臺機器上的開始時間sbj確定時,對應的第一道工序aj在第一臺機器的位置也唯一確定。因此只考慮每個工件的第二道工序bj,即此問題等價于1‖∑Uj。對于極小化誤工工件數的問題1‖∑Uj,1968年Moore給出了一個多項式時間的最優算法。 定理4.2.1 算法H可以得到問題F2|exactlj,aj=bj,lj=2a|∑Uj的最優排序如圖5所示。 圖5 最優排序Fig.5 Optimal sorting 證明:不妨d1≤d2≤…≤dn,設P=(S,F)為算法所得的排序,其中S為按期完工工件集,F為誤工工件集,即算法在第③步中刪除的工件集合。不妨設F≠Φ,令工件k是算法第1次執行到第③步時找到的延誤工件,于是i就是算法刪除的第1個工件。由算法規則可知 1,…,i-1沒有誤工工件,下面首先證明:存在最優排序P′=(S′,F′)(S′和F′定義同上),使得i∈F′。 設P′=(S′,F′)是一個最優排序且i∈S′。并記F′=π(r+1)…π(n),S′=π(1)…π(r),不妨認為dπ(1)≤dπ(2)≤…≤dπ(r)。再由于d1≤d2≤…≤dn,所以一定存在m使得: i∈{π(1),…,π(m)}?{1,…,i},{π(m+1),…,π(r)}?{i+1,…,n}。并且由i定義,序列1,…,i產生延誤,因而{π(1),…,π(m)}≠{1,…,i}。于是存在1≤h≤i,h?{π(1),…,π(m)},所以有: {π(1),…,π(m)}∪{h}{i}?{1,…,k}{i}。 由此可知{π(1),…,π(m)}∪{h}{i}按照EDD排列后不產生延誤,且這些工件的總加工時間比{π(1),…,π(m)}中工件總加工時間減少了,這表明在上述工件序列之后加上原來的π(m+1),…,π(r)也不產生誤工工件。換句話說,我們構造出了一個誤工工件數與P′相同但i是誤工工件的排序,即得到了滿足要求的最優排序。 根據上面這個結論,對工件數目作歸納,證明定理結論:顯然當n=1時,該算法可以得到最優排序。假設算法對工件數為n-1的實例均能找到最優排序,則對任一工件數為n的實例,設P=(S,F)是算法所得的排序,工件i∈F如上定義。所以存在一個最優排序P′=(S′,F′),使得i∈F′,顯然有|S|≤|S′|。另一方面,考慮實例{1,…,i-1,i+1,…,n},由歸納假設及算法規則,算法得到的排序形如P=(S,F{i})且是一個最優排序。再注意到P′=(S′,F′{i})是該實例的可行排序,所以又可得到|S|≥|S′|。因此|S|=|S′|,算法對n個工件的實例也得到最優排序。 當aj=bj=a,lj=ka時,sb1=(k+1)a。因為每個工件的第一道工序aj在第一臺機器上執行,第二道工序bj在第二臺機器上執行,并且它們之間存在的是精確時間延遲,所以當第二道工序bj在第二臺機器上的開始時間sbj確定時,對應的第一道工序aj在第一臺機器的位置也唯一確定。因此只考慮每個工件的第二道工序bj,即此問題等價于1‖∑Uj。對于極小化誤工工件數的問題1‖∑Uj,1968年Moore給出了一個多項式時間的最優算法。 定理4.3.1 算法H可以得到問題F2|exactlj,aj=bj,lj=ka|∑Uj的最優排序如圖6所示。 圖6 最優排序Fig.6 Optimal sorting 證明:不妨d1≤d2≤…≤dn,設P=(S,F)為算法所得的排序,其中S為按期完工工件集,F為誤工工件集,即算法在第③步中刪除的工件集合。不妨設F≠Φ,令工件k是算法第1次執行到第③步時找到的延誤工件,于是i就是算法刪除的第1個工件。由算法規則可知 1,…,i-1沒有誤工工件,下面首先證明:存在最優排序P′=(S′,F′)(S′和F′定義同上),使得i∈F′。 設P′=(S′,F′)是一個最優排序且i∈S′,并記F′=π(r+1)…π(n),S′=π(1)…π(r)。不妨認為dπ(1)≤dπ(2)≤…≤dπ(r),再由于d1≤d2≤…≤dn,所以一定存在m使得: i∈{π(1),…,π(m)}?{1,…,i},{π(m+1),…,π(r)}?{i+1,…,n}。 并且由i定義,序列1,…,i產生延誤,因而{π(1),…,π(m)}≠{1,…,i}。于是存在1≤h≤i,h?{π(1),…,π(m)},所以有: {π(1),…,π(m)}∪{h}{i}?{1,…,k}{i}。 由此可知{π(1),…,π(m)}∪{h}{i}按照EDD排列后不產生延誤,且這些工件的總加工時間比{π(1),…,π(m)}中工件總加工時間減少了,這表明在上述工件序列之后加上原來的π(m+1),…,π(r)也不產生誤工工件。換句話說,我們構造出了一個誤工工件數與P′相同但i是誤工工件的排序,即得到了滿足要求的最優排序。 根據上面這個結論,對工件數目作歸納,證明定理結論:顯然當n=1時,該算法可以得到最優排序。假設算法對工件數為n-1的實例均能找到最優排序,則對任一工件數為n的實例,設P=(S,F)是算法所得的排序,工件i∈F如上定義。所以存在一個最優排序P′=(S′,F′),使得i∈F′,顯然有|S|≤|S′|。另一方面,考慮實例{1,…,i-1,i+1,…,n},由歸納假設及算法規則,算法得到的排序形如P=(S,F{i})且是一個最優排序。再注意到P′=(S′,F′{i})是該實例的可行排序,所以又可得到|S|≥|S′|。因此|S|=|S′|,算法對n個工件的實例也得到最優排序。 主要研究了帶精確時間延遲的兩臺機流水作業排序問題。第一道工序在第一臺機器上執行,第二道工序在第二臺機器上執行,分別以極小化加權總完工時間,最大延誤時間和總延誤數為目標函數,設計了最優算法。 需要進一步研究和考慮的問題還有: ①F2|exactlj|∑wjCj帶確切延誤的兩臺機流水作業排序問題,目標是加權總完工時間。 ②F2|exactlj|Lmax帶確切延誤的兩臺機流水作業排序問題,目標是極小化最大延誤時間。 ③F2|exactlj|∑Uj帶確切延誤的兩臺機流水作業排序問題,目標是總延誤數。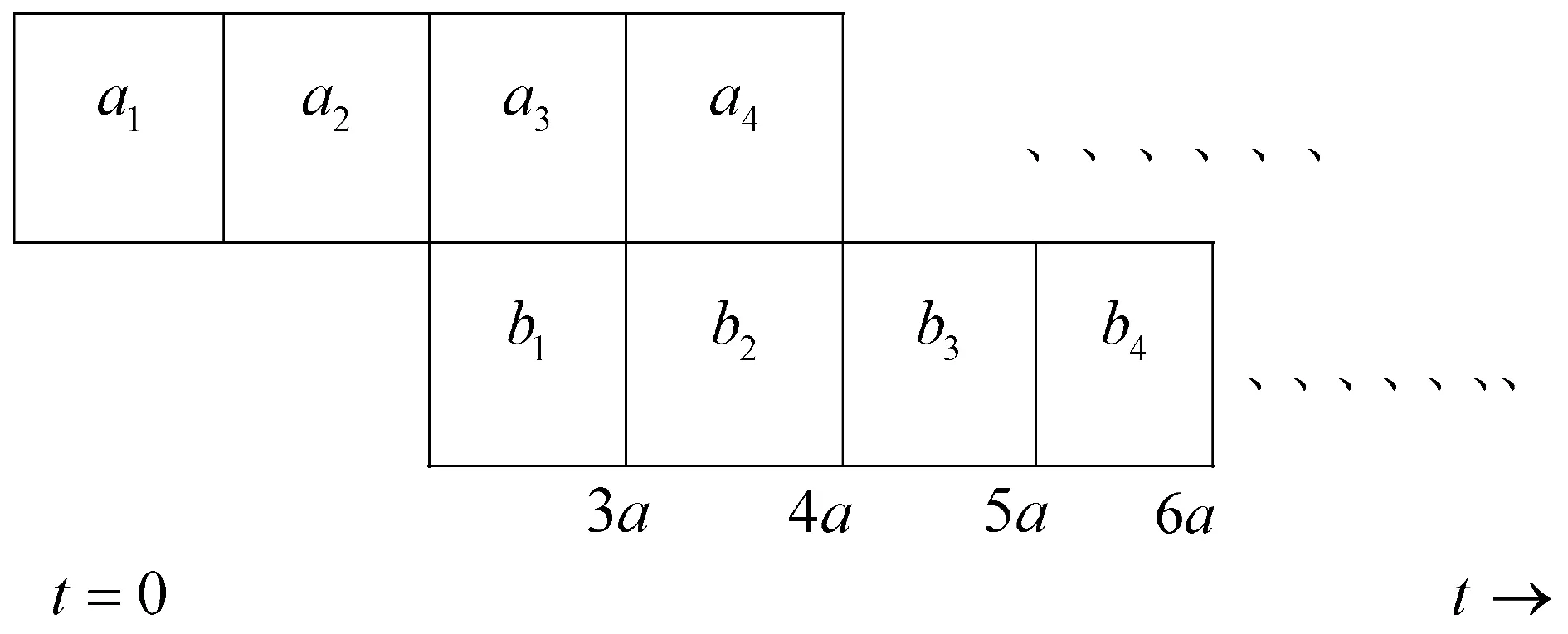
2.2 F2|exact lj,aj=bj,lj=2a|∑wjCj的最優算法
2.3 F2|exact lj,aj=bj,lj=ka|∑wjCj的最優算法
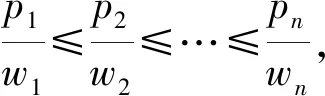

3 F2|exact lj,aj=bj,lj=ka|Lmax的最優算法
3.1 F2|exact lj,aj=bj=lj=a|Lmax的最優算法
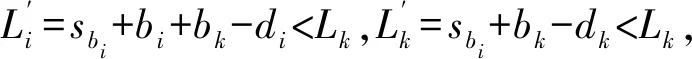
3.2 F2|exact lj,aj=bj,lj=2a|Lmax的最優算法
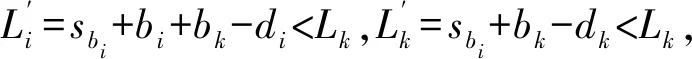
3.3 F2|exact lj,aj=bj,lj=ka|Lmax的最優算法
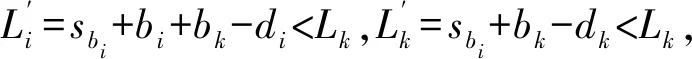
4 F2|exact lj,aj=bj,lj=ka|∑Uj的最優算法
4.1 F2|exact lj,aj=bj=lj=a|∑Uj的最優算法
4.2 F2|exact lj,aj=bj,lj=2a|∑Uj的最優算法
4.3 F2|exact lj,aj=bj,lj=ka|∑Uj的最優算法
5 結語

