數學思維能力在高中數學教學中的培養

蔡 毅

一、數學思維的概述

所謂的數學思維，就是指對數學符號及文字等相關數學知識進行靈活應用，以此建立良好的數學認知結構，并形成一種具備較高系統性、邏輯性以及推理性等數學特性的思維模式，這種數學思維模式的形成能夠讓學生在解題過程中快速發散自身的思維，思考出相應的解題思路，提高自身的解題效率，而且學生具備較高的數學思維能力，也能夠加深對數學知識的理解，使其能夠牢固掌握所學知識。數學思維也具備一定的特點，其中主要包括兩方面。

1.數學思維具有整體性。數學知識的應用極為廣泛，不僅在日常生活中得到了應用，而且還在物理、化學等各種理科領域中也得到了充分的應用。數學知識能夠根據各種實際應用需求進行類型劃分，而不論怎樣劃分，這些數學知識在應用過程中都脫離不了相應的數學思維，因為數學思維是數學知識應用的核心，它能夠將所有的數學知識有效整合在一起，以此達到有效解決相關問題的作用，將數學知識的作用充分發揮出來。

2.數學思維具有一定的差異性。對于數學思維來說，其自身并沒有固定的形態或者表現形式，數學思維都是在學習過程中逐漸形成的。但是，由于人們觀察事物的角度都各有不同，再加上思考方式也各不一樣，就使得數學思維形成的形式以及應用的方式也有一定的差別，而不論學生之間具備什么樣的數學思維能力，但都殊途同歸，都能夠促進學生數學學習能力的提高。

二、數學思維能力培養的有效策略

1.鼓勵學生開放解題思路，避免問題答案的固定化

高中教師若想有效培養學生的數學思維能力，就要在數學教學過程中開拓學生的思維，拓展學生的解題思路，避免學生在解題過程中思維受到固化。多數學生在解決數學問題的過程中經常遇到困難，在這種時候，學生會習慣性地查閱參考答案，或者在數學課文中查找相關例題及知識點，然后再按照查找出來的思路進行解題，這樣的學習方式雖然能夠有效解決數學問題，但是學生自身的思維將會被限制在固定的范圍之內，這就容易讓學生形成相應的思維定式，影響學生創新思維能力的形成與發展，同時也會對學生數學思維能力的提高產生較高的影響。基于此，高中教師在對學生進行數學教學時，要鼓勵學生開放自己的解題思路，引導學生結合相關數學知識發散自身的思維，讓學生的思路得到一定的拓展，使得學生能夠將所學的數學知識靈活應用在解題過程中。

2.采用數形結合的教學方式，提高學生思維的靈活性

對于數學知識來說，抽象性是其主要特點，而且高中數學知識具備更高的抽象性，學生理解起來難度也會更大，這就對學生的數學邏輯思維能力有了更高的要求，而高中教師若想提高數學教學的質量與效率，首先就要培養學生的數學思維能力，讓學生能夠更好地理解數學知識，這樣才能夠促進學生數學學習水平及效率的提高。由此可見，數學思維能力在高中生的學習過程中有著非常重要的促進作用。基于此，高中教師在數學教學過程中要重視培養學生的數學思維能力，轉變自身的應試教育思想，結合學生的學習需求，對以往傳統的數學教學方式進行科學合理的改進，同時還要明確高中數學知識中的內部聯系，并向學生進行講解，以此優化學生的數學認知結構。

另外，高中教師可以將數形結合的教學方式融入整個數學教學之中，在對學生講解數學問題的過程中，教師可以將圖形與數字有效結合起來剖析解題思路，引導學生形象思維與抽象思維之間的互相轉化，讓學生能夠通過這種方式牢固掌握所學知識，同時也能夠利用這種思維轉化方式提高解題效率，進而促進學生數學思維靈活性的提高。比如，以人教版的高中數學教材為例，高中教師在對學生講解“已知集合A=｛x|0＜x＜5｝，B=｛x|a＜x＜2a｝≠Φ，(a∈R)，若A?B，求a的取值范圍”這一類的集合問題時，可以利用數軸加深學生對問題的理解，培養學生利用圖形解決數學問題的思維方式。教師可以在學生解題過程中引導其畫出數軸(如圖3-2)，這樣可以加深學生對數學問題的理解，同時也能夠讓學生快速推理出問題的答案，當A?B時，a有三種情況：a＜0，5＜2a，a＜2a，由此得出a無解。這樣的解題過程既能夠提高學生的解題速度，也能夠讓學生養成數形結合的思維能力，提高學生自身思維的靈活性。

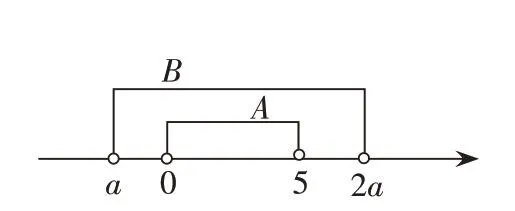
圖3 -2

三、總結

總之，高中階段是學生學習過程中非常重要的時期，也是學生在思維能力方面能夠實現由量轉變到質的關鍵時期，基于此，高中教師在對學生進行數學教學時，要重視對學生數學思維能力的培養，提高學生的數學學習能力，促進學生學習的高效發展。