核心素養(yǎng)導向下的高考數(shù)學命題創(chuàng)新探究

孔令潤?談濤　劉杰

近日，中共中央、國務院印發(fā)了《深化新時代教育評價改革總體方案》，提出建立科學的、符合時代要求的教育評價制度和機制，為高考評價機制改革提供理論支撐和改革方向。高考命題在改革中不斷探索創(chuàng)新，折射出國家對于新時代全面育人目標的要求，以《中國高考評價體系》為依托，以學科核心素養(yǎng)為導向，通過情境和情境活動兩類載體，實現(xiàn)“四層”考查內容和“四翼”考查要求。拓展試題情境來源，巧設情境呈現(xiàn)方式和創(chuàng)新設問方式，已成為基于核心素養(yǎng)的高考命題改革和創(chuàng)新的基本原則。高考數(shù)學學科的情境包括三類：課程學習情境、探索創(chuàng)新情境和社會實踐情境，三種問題情境在高考中發(fā)揮不同作用。以情境創(chuàng)新試題孕育創(chuàng)新意識，對于高中數(shù)學教學和備考具有現(xiàn)實指導意義。本文僅從四個方面對情境試題創(chuàng)新方向和策略進行探究。

一、利用時事熱點問題為背景創(chuàng)設體育情境

高考強調學以致用。“在命題時應堅持理論聯(lián)系實際的原則，使用貼近時代、貼近社會、貼近生活的素材，選取日常生活、工業(yè)生產、國家發(fā)展、社會進步中的實際問題”，情境類試題在近幾年高考中出現(xiàn)頻率呈現(xiàn)逐年加大趨勢，它們從不同維度和視角將數(shù)學知識與社會熱點緊密結合，考查學生的理性思維，數(shù)學應用和數(shù)學探索能力，體現(xiàn)素養(yǎng)導向和時代特征。下面是以體育素材為情境命制的一道創(chuàng)新題。

2020年9月13日，斯諾克2020/2021賽季大幕開啟，斯諾克臺球比賽以其特有的魅力而被廣大群眾所喜愛，比賽中擊球規(guī)則可簡化為：球桌上共有15個紅球和6個彩球（黃、綠、咖啡、藍、粉、黑），參賽選手需先擊打紅球，然后再擊打彩球，之后紅球和彩球依次間隔擊打。若某次比賽中，參賽者開局連續(xù)打進10個球，則不同的擊球順序共有____種。

分析：計數(shù)原理是數(shù)學中的重要研究對象之一，排列、組合是解決計數(shù)問題的最基本、最重要的方法，它們?yōu)榻鉀Q很多實際情境中的問題提供了思想和工具。實際生活中計算某種情形可能出現(xiàn)的種數(shù)，是最常見的設問方式，有時需要添加具有一定約束的條件，而斯諾克臺球比賽中的擊球順序需滿足一定的規(guī)則要求，可作為考查計數(shù)原理知識較為合理的載體。

本題的命題素材所隱含的數(shù)學知識（計數(shù)原理）和方法（排列數(shù)計算）均直接源自學生已有的學習儲備，通過對擊球規(guī)則的簡化，提出了計算不同擊球順序的種數(shù)的問題。本題把數(shù)學核心知識的考查與體育緊密聯(lián)系起來，體現(xiàn)“高考內容改革要貫徹五育并舉的教育方針，完善覆蓋德智體美勞全面發(fā)展要求的考試內容體系”的指導思想，貫徹高考命題“鑄魂育人”的要求。試題情境新穎，問題設計難度適中，體現(xiàn)基礎性，在考查學生的閱讀理解能力的同時，激發(fā)他們對體育運動的興趣。

二、用跨學科知識為背景創(chuàng)設學科交叉情境

在知識網絡的交匯點設計試題，增強考核內容的基礎性和綜合性。在近幾年的高考試題中可以發(fā)現(xiàn)有以化學、生物、物理、地理、醫(yī)學等知識融合為情境載體，考查數(shù)學核心知識和關鍵能力的題目。下面是以高中物理知識為情境命制的一道創(chuàng)新題。

根據法拉第電磁感應定律，閉合電路中瞬時感應電動勢false的大小，跟穿過這一電路的磁感應強度false與該閉合電路的面積false的乘積的瞬時變化率成正比，即false，已知false，false，false，則當false時，_________ false。

分析：求物理量的瞬時變化率需要用到導數(shù)這一工具，而物理學科中的法拉第電磁感應定律涉及磁通量的瞬時變化率的問題，磁通量與磁感應強度和閉合電路面積有關，且高中物理對這一知識的要求一般是磁感應強度不變或者閉合電路面積不變，學生在學習過程中可能會對這兩者都發(fā)生變化時的問題感到好奇，但又不知該如何解決。

本題選取物理學科中的法拉第電磁感應定律為命題情境，與高中數(shù)學中的函數(shù)求導乘法法則問題建立關聯(lián)，屬于對基本知識和運算能力的考查。與物理中求瞬時感應電動勢不同的是，試題中的磁感應強度false與閉合電路的面積false均隨著時間false的變化而變化。試題設計巧妙，在考查數(shù)學知識的同時，也有助于加深對物理學科中法拉第電磁感應定律的理解，凸顯了數(shù)學的工具性特征，展現(xiàn)數(shù)學的應用價值，符合跨學科命題的特點。

三、用傳統(tǒng)文化及數(shù)學史等為背景創(chuàng)設文化情境

數(shù)學文化是對數(shù)學知識、技能、能力和素養(yǎng)的高度概括，無論是中國文化的源遠流長，還是世界歷史的百家爭鳴，數(shù)學都在其中留下了不可磨滅的寶貴成就。數(shù)學文化是一種理性的藝術，利用傳統(tǒng)文化及數(shù)學史等為背景創(chuàng)設文化情境類試題，可以讓學生感受先賢天馬行空的想象和精益求精的科研精神，從而勇于創(chuàng)新，不斷求索。縱觀近幾年的高考數(shù)學命題，數(shù)學文化類試題已經從開始引導到逐步滲透，逐漸浸潤到數(shù)學的每個模塊和專題中，這也是順應新課改和新高考對育人方式變革要求的又一舉措。

命制符合新課改導向的數(shù)學文化情境試題，可以采用先選取素材，再確定考查的知識點，或者先確定考查知識點再反方向尋找素材的方法，下面以先選取素材再確定考查知識點的方法為例說明。

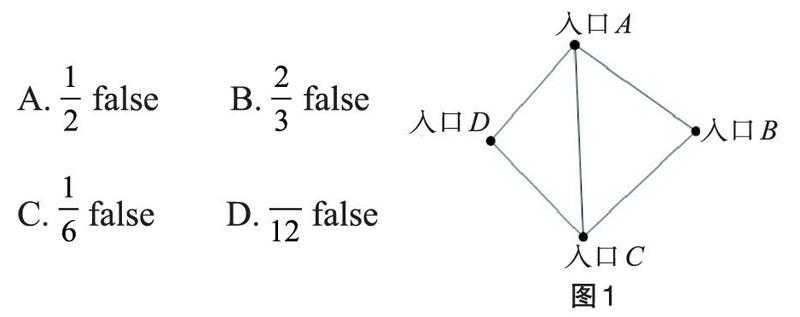
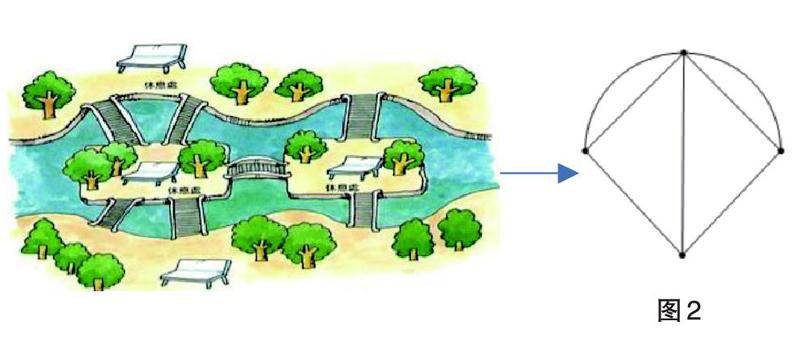
18世紀初普魯士的哥尼斯堡有一條河穿過，河上有兩個小島，有七座橋把兩個島與河岸聯(lián)系起來。當?shù)亓鱾髦S多與七座橋有關的傳說，其中一個是這樣的：能否不重復、不遺漏地一次走完七座橋。1736年，29歲的歐拉向圣彼得堡科學院遞交了《哥尼斯堡的七座橋》的論文，在解答問題的同時，開創(chuàng)了數(shù)學的一個新的分支—圖論與幾何拓撲。同學A和B在如圖1所示的花園中模擬這個問題，他們同時從四個入口中任意兩個不同的入口出發(fā)，則他們都可以不重復、不遺漏地游覽完整個花園的五條路的概率是___________。

A.falseB.false

C.falseD.false

分析：本題的材料背景來源于《人教A版 選修3-1 數(shù)學史選講》，故事流傳性很廣。被選入小學、初中、高中課本，很好地體現(xiàn)了數(shù)學的連續(xù)性和延展性。材料中歐拉從這個問題開創(chuàng)出了數(shù)學新的分支—圖論與幾何拓撲，是對現(xiàn)有問題經過思考后的總結升華，整個過程引導、啟發(fā)學生用發(fā)展的、關聯(lián)的眼光看問題。選定素材后，即可確定材料想要考查的知識點，材料中“怎樣才能不重復、不遺漏地一次走完七座橋”暗含了兩個核心關鍵“能不能完成”以及“如何完成”，這其中涉及了“選擇”和“事件”，與概率知識點有很高的關聯(lián)性，故可以創(chuàng)設如下命題原型。

從圖2四個點出發(fā)可以不重復、不遺漏地走完所有線路的概率是多少？

本題在情境問題設計方面，受學生是否看過歐拉解決這個問題的方法影響，難度會有較大變動，不符合公平性原則，故設計的問題可以考慮減弱學生在判斷是否能完成上的難度，增加對概率知識的考查，即可得到上述例題。當然，也可以通過改變設問方式適當增加難度。

四、用貼近生活的熟悉背景創(chuàng)設實際應用情境

給一些簡單的問題賦予應用的情境是試題改編的一種方式，合適的問題情境可以賦予枯燥的數(shù)學知識以鮮活的生命力。在賦予一定的應用情境的同時，還需要在數(shù)據、數(shù)量關系等方面進行再加工，使之貼近生活實際。

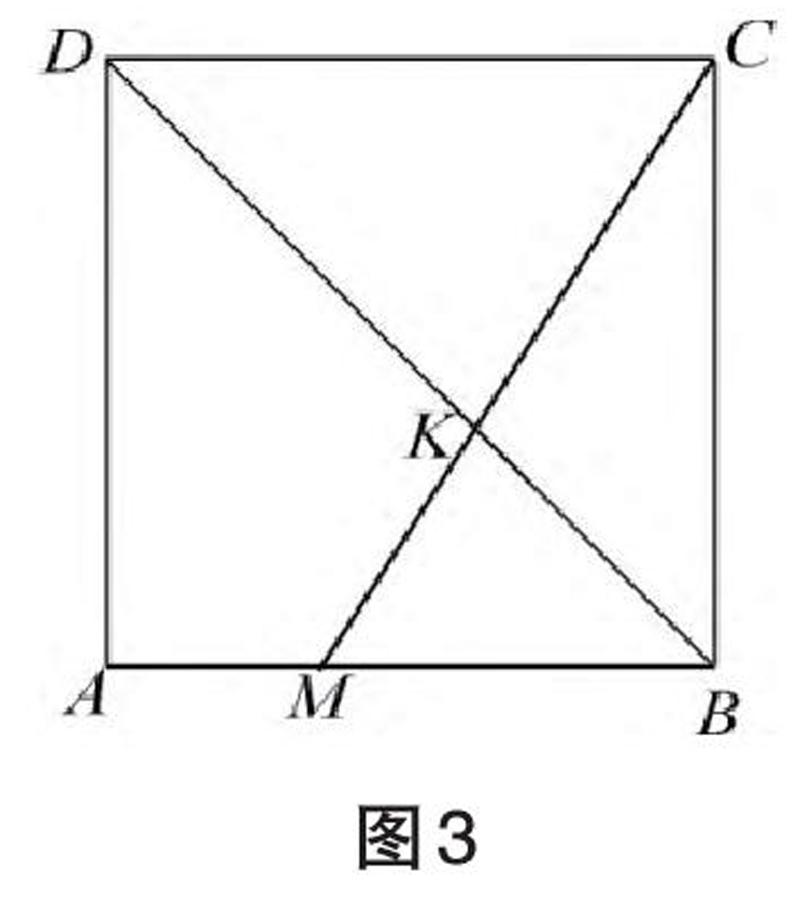
原題：如圖3，K是邊長為1的正方形ABCD的對角線BD上一點，連接CK，并延長交邊AB于點M，求ΔCKD與ΔBKM的面積和的最小值及此時的DK長。

加載情境后的改編題：如圖3，某園林規(guī)劃部公司計劃在一塊邊長為2百米的正方形區(qū)域ABCD內設計兩塊綠化區(qū)域和兩塊休閑區(qū)域，具體設計的方案為：在對角線BD上取一點K（不含端點），連接CK并延長交線段AB于點M，ΔCKD與ΔBKM為綠化區(qū)，其余區(qū)域均為休閑區(qū)，已知綠化區(qū)每平方百米造價為50萬元，休閑區(qū)每平方百米造價為25萬元，設DK長為x百米，綠化區(qū)和休閑區(qū)的總造價為false萬元。

（1）求函數(shù)false的解析式，并指出其定義域;

（2）當DK長為多少時，總造價最少？最少為多少？

分析：原題是一個純數(shù)學情境的幾何問題，賦予應用情境后改編變成有一定閱讀量、數(shù)量關系也較原題復雜的應用題，要求學生能夠從實際應用情境中抽象與提取數(shù)學問題，建構與解決相應函數(shù)模型，屬于較復雜的生活實踐情境，對學生的數(shù)學閱讀與理解能力、信息識別與提取能力有較高要求。改編后的試題在綜合性和應用性層次上考查學生的數(shù)學建模、數(shù)學運算等素養(yǎng)以及對新問題的探究能力，體現(xiàn)了數(shù)學的應用價值和在解決實際問題中的作用。

總之，試題情境的創(chuàng)設，既為提高試題質量提供技術保障，也為實現(xiàn)價值引領、素養(yǎng)導向、能力為重、知識為基的命題理念提供方法保障。在創(chuàng)設試題情境時，多結合社會現(xiàn)實，反映數(shù)學應用的廣闊領域，體現(xiàn)數(shù)學文化和數(shù)學應用的領域，回歸學生發(fā)展，回歸數(shù)學本質，回歸教育規(guī)律，回歸實際背景。情境材料所隱含的知識與方法，必須與試題的考查內容、考查要求相一致，情境的設置和對考生解題思路的預設應當符合中學生實際的認知水平，使考生能夠應用所學知識對題干內容進行深層挖掘和分析，其作答應該能夠體現(xiàn)分析和解決問題的思維過程，使數(shù)學的重點知識、技能方法成為考生分析、解答問題的有效工具，培養(yǎng)考生靈活運用所學知識解決各類問題的良好思維習慣，為其今后的成長和發(fā)展提供智力支持。研究情境類試題的創(chuàng)新策略，對提高數(shù)學教師創(chuàng)新型試題的命題意識和培養(yǎng)學生數(shù)學創(chuàng)新能力是有益的。

（作者單位：科大訊飛）

責任編輯：李莎

lis@zgjszz.cn