量子化學計算原理及其應用

陳奕馳

(西北工業大學附屬中學 西安 710000)

一、量子化學的發展

量子化學是利用量子力學研究化學問題，其核心是精確求解薛定諤方程。在量子力學中，粒子的狀態用波函數（概率分布函數）來描述。為了描述粒子狀態變化的規律，需要找出波函數所滿足的運動方程，薛定諤方程夠滿足上述要求。

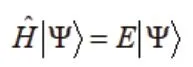
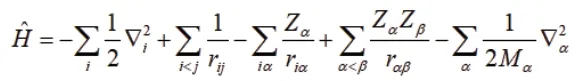
其中第一項表示電子動能，第二項是電子互斥勢，第三項是電子與原子核的吸引勢，第四項是原子核之間的互斥勢，第五項是原子核的動能項。

上述公式都是采用原子單位，原子單位可以使得各種計算公式中不需要涉及單位轉換，一方面使得代碼簡潔，另一個方面也可以避免額外的計算帶來的精度的損失。上述公式中電量的原子單位就是電子所帶電量的絕對值。能量的原子單位是hartree 相當于2625.500 kJ/mol。

量子化學的核心問題是求解分子體系的薛定諤方程，但是由于沒有辦法精確求解，在實際求解中會用到各種近似，其中最常用的近似是Born-Oppenheimer 近似。[1]考慮到原子核的質量是電子質量的1780倍。原子核的運動相對于電子的運動非常慢，因此，把原子核的運動認為是靜止的。此時，對于公式2中的哈密頓量。原子核的動能項為0，原子核之間的相互作用就是常數了。這樣只要考慮電子的運動，原子核的位置作為參數處理，能夠減少計算量，使得關注點在電子的運動。除了Born-Oppenheimer近似外，還有有限基組近似。也就是說，我們在描述一個體系的時候，需要無數的基（向量）才能準確描述，但是如果做泰勒展開的話，我們只保留展開式的前幾項，后面的項都忽略，這樣也能極大減少計算量。

Hartree-Fock方法，又稱為自洽場迭代方法，是量子化學求解薛定諤方程的基礎方法，其他的方法都是在HF方法的基礎上發展而來的。我們觀察公式1可以發現。目前我們只知道H的表達式，而需要求解能量E，波函數 。一個公式中兩個未知數，而且是等式兩邊都有需要求解的波函數。自洽場迭代的思想如下。首先，對波函數 進行一個猜測，這樣，公式的左邊H和波函數都已知了，此時我們把波函數記為，通過薛定諤方程，我們可以求出公式右邊的E和波函數。我們把此次求得的結果記為E1和，然后我們把帶入到公式的左邊，繼續求解，得到E1和，如此循環下去，直到En和En+1之間的差足夠小。這個差值是我們自己設置的。一般是要小于1kJ/mol。此時可以認為，我們求出了合適的能量E和波函數。這個過程是不斷循環迭代的，所以稱為自洽場迭代方法。實際計算的時候是矩陣計算，需要對矩陣進行對角化計算。

量子化學計算精度的關鍵在于理論方法和基組兩個部分。如圖所示：

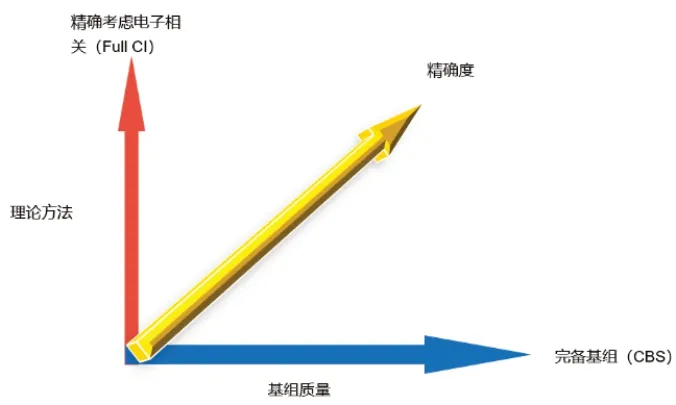
圖1 量子化學計算精度與理論方法、基組的關系

考慮到計算的體系大小和計算的資源等，我們需要做的是理論方法能夠和基組大小達到匹配。高精度的理論方法配合高質量的基組，否則就是一種浪費。

除了Hartree-Fock計算方法外，還有一種常見的計算方法是密度泛函方法。密度泛函方法是目前實際計算中廣泛使用的方法，能夠在可以接受的時間范圍內，給出較為精確的計算結果。密度指電子數密度；泛函是說能量是電子密度的函數，而電子密度又是空間坐標的函數；函數的函數，是為泛函（Functional）。[2]密度泛函理論是一種通過電子密度研究多電子體系電子結構的方法。具體到操作中，密度泛函理論通過各種各樣的近似，把難以解決的包含電子-電子相互作用的問題簡化成無相互作用的問題，再將所有誤差單獨放進一項中（XC Potential），之后再對這個誤差進行分析。下圖給出了計算精度和時間花費的關系。

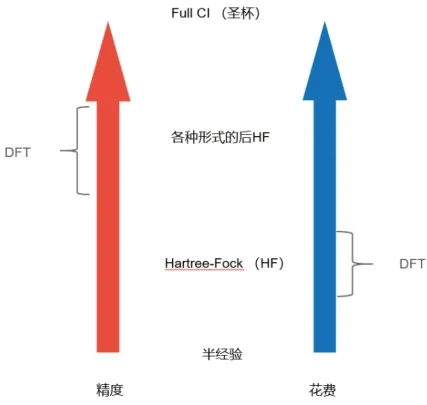
圖2 計算精度與計算時間的關系

二、Gaussian

Gaussian是最早的一批量子化學計算程序，由1998年諾貝爾獎獲得者John A.Pople從1970年起在卡內基梅隆大學主導開發。該軟件功能全面，配合GaussView圖形界面。輸入文件的編寫是所有主流量化程序中最簡單的，能夠實現很多的功能。包括對于基態、激發態、反應過渡態的幾何結構優化；基態、激發態能量計算，化學鍵能計算，電子解離能和親合能的計算；對于紅外光譜，拉曼光譜，核磁共振譜的光譜計算；偶極矩，電荷分布，電荷密度，熱力學參數等的計算。

三、基組

具體計算的時候，波函數是用原子軌道線性展開的。原子軌道是由基組構成的。考慮到不同的計算要求，需要對基組添加極化函數和彌散函數。極化函數是用來描述分子軌道發生很大形變時，更準確地描述。例如，我們知道s軌道是個球形的，但是如果收到周圍電荷的影響，球形可能形變成橢球形，此時，用極化函數可以描述這種變形。另外，在電子遷移的過程中，電子會彌散到整個空間，這個時候用彌散函數描述這種大的范圍的軌道性質，才能更真實反應體系的性質。同時需要注意的是，基組的變大會使得計算花費的時間增大很多。

（一）實驗過程

通過計算振動頻率判斷乙酸、乙醛、丙酮中的羰基強弱。

在GView軟件中搭建乙酸分子，點擊Calculate，Job Type設置為Opt+Freq，Method設置為DFT下的B3LYP法和3-21G基組，打開Gaussian03W進行計算，再用GView打開輸出文件，在Result一欄點擊Vibrations，在彈出的對話框中設置Show Displacement Vectors，點擊各個振動頻率，觀察選中哪一個頻率時箭頭顯示為羰基的振動頻率，將其記錄下來。完成后對乙醛、丙酮進行相同操作。以上全部完成后，將基組改為6-31G，方法不變，重復全部操作。

（二）實驗結果

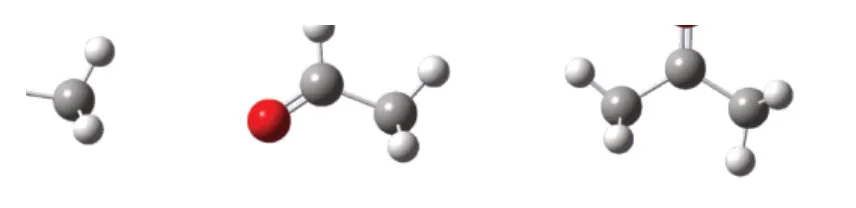
圖3 B3LYP/6-31G 優化后的（a）乙酸；（b）乙醛；（c）丙酮

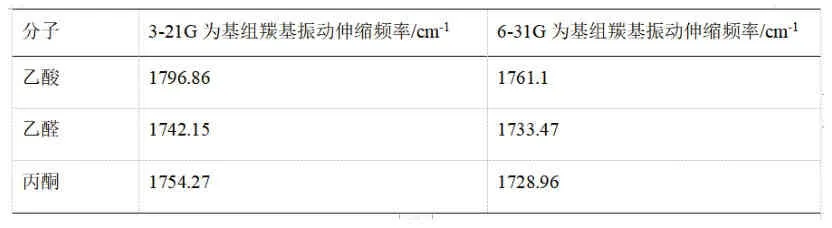
表1 B3LYP/6-21g//6-31g乙酸、乙醛、丙酮羰基的振動伸縮頻率的計算結果

羰基由強到弱排列順序：乙酸、乙醛、丙酮。

四、結果討論

由于化學鍵振動伸縮頻率越高強度越大，我們從計算結果可以得知在使用B3LYP方法的前提下，使用3-21G基組計算時得出的結論是羰基強度從強到弱順序為乙酸、丙酮、乙醛，使用6-31G基組時從強到弱順序則為乙酸、乙醛、丙酮。要試圖解釋此結果可以考慮從羰基氧和羰基碳原子的電荷分布入手，而這正是從輸出文件中可以得到的，具體數據見表2和表3。

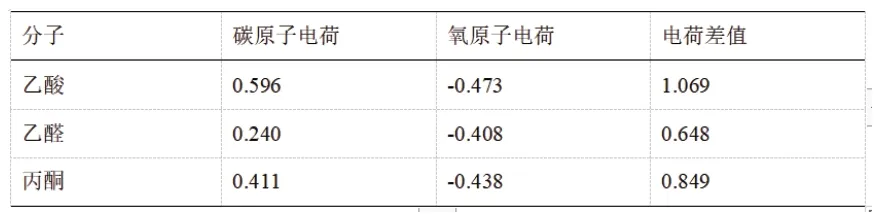
表2 B3lyp/3-21G計算后的乙酸、乙醛和丙酮中羰基碳和羰基氧的電荷分布

由表2可見，用3-21G基組算出的羰基碳氧電荷差值的大小順序與羰基的相對強弱順序是吻合的，從靜電作用角度理解，碳原子和氧原子間更大的電荷差距使得正負電荷之間的庫倫相互作用增強，對于鍵能的增益更加明顯。

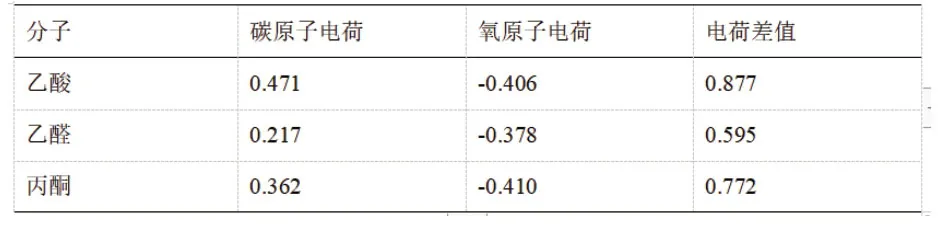
表3 B3LYP/6-31G 計算后的乙酸、乙醛和丙酮中羰基碳和羰基氧的電荷分布

由表3可知，從羰基碳氧電荷差值大小順序來看，6-31G基組算得的結果與3-21G基組相同，皆為乙酸＞丙酮＞乙醛，但是從振動伸縮頻率上看，6-31G基組算得的羰基強弱順序為乙酸＞乙醛＞丙酮，與3-21G的結果以及6-31G的電荷差值結果不符。因為盡管3-21G與6-31G屬于不同的基組，但是它們都屬于劈裂價鍵基組，對這兩個基組而言，每個價層電子軌道都會被劈裂為兩個基函數，3-21G基組中價層電子軌道由3個和1個高斯型函數線性組合而成，每個內層電子軌道由3個高斯型函數線性組合而成，而6-31G基組中后者為6個，價層電子軌道由3個和1個高斯型函數線性組合而成，每個內層電子軌道由6個高斯型函數線性組合而成，二者的結果為何不同還需要進一步探索。

五、結束語

計算化學的發展幫助我們更好地理解實驗現象并且給出定量的解釋。但是同時，我們要意識到很多時候，計算的結果和實驗結果有出入的時候，要明確我們計算的物理量是否就是實驗上的。比如，我們研究是羰基的鍵的活潑性，而不是羰基的鍵和鍵共同的。我們計算的頻率是雙鍵的頻率。因此，要做出區分。Gaussian軟件結合Gaussview軟件的作圖能幫助快速計算，并給出定量的結果去討論，而計算結果需要結合有機化學的知識去進一步分析。