一種成績修正算法在《資源與環(huán)境材料學(xué)》課程考核中的應(yīng)用

孫桂林，陶素芬，徐浩明，呂寧寧

（安徽工業(yè)大學(xué) 冶金工程學(xué)院，安徽 馬鞍山）

一 引言

《國家中長期教育改革和發(fā)展規(guī)劃綱要(2010～2020年)》中明確指出，教育改革發(fā)展的核心任務(wù)是提高教育質(zhì)量，樹立科學(xué)的質(zhì)量觀，建立以提高質(zhì)量為核心的教育發(fā)展觀；強(qiáng)調(diào)更新培養(yǎng)觀念、創(chuàng)新培養(yǎng)模式、改革教育質(zhì)量評價和人才評價制度[1]。教學(xué)改革的重要舉措是完善科學(xué)合理的課程考核評價體系[2]。高校學(xué)生的課程考核評價通常由課程成績來衡量。

課程成績是對教學(xué)效果的一種重要的反饋和檢驗，與任課教師的教授能力與態(tài)度、學(xué)生的學(xué)習(xí)能力與態(tài)度以及試題的難易程度等密切相關(guān)，是檢驗教學(xué)質(zhì)量、衡量教學(xué)效果的重要手段。目前許多高校都把課程成績是否符合正態(tài)分布作為教與學(xué)的效果評價唯一指標(biāo)[3]。

正態(tài)分布又稱Gauss分布，是一種重要的描述連續(xù)型隨機(jī)變量最重要的分布。美國教育學(xué)家Carroll于1963提出了課程成績呈正態(tài)分布的概念[4,5]，“他闡明了這樣一種事實，如果在某一學(xué)科（數(shù)學(xué)、科學(xué)、文學(xué)或歷史）中，學(xué)生的能力傾向是正態(tài)分布的，并且為所有學(xué)生提供了完全一樣的教學(xué)徽學(xué)的數(shù)量與質(zhì)量、可用于學(xué)習(xí)的時間都一樣，那么在適當(dāng)?shù)某煽儨y量中，最終結(jié)果將呈正態(tài)分布”。

眾所周知，成績是一個相對的標(biāo)準(zhǔn)，不同的試題難度及評分標(biāo)準(zhǔn)，會造成不同的成績，題目容易可能使全班成績都在90分以上，題目難又會使全班成績在60分以下，所以同一科目不同批次、甚至同一考生不同科目的成績，都很難進(jìn)行比較。根據(jù)教育測量學(xué)和考試學(xué)的理論[6,7]，試題的難度以能使絕大多數(shù)學(xué)生達(dá)到教學(xué)大綱規(guī)定的基本要求為宜，考生的成績分布也應(yīng)大致呈正態(tài)分布，優(yōu)秀率與不及格率應(yīng)各占10%左右。然而在實際教學(xué)中，即使教師在編制試卷時已十分小心、注意了對試題難度的掌握，但仍難保證考試分?jǐn)?shù)的分布十分令人滿意，特別是難以控制學(xué)生的優(yōu)秀率及不及格率各為10%左右，此外教師也無法做到兩份試卷的難度完全相同。那么，是否存在一種簡單、可靠的換算方法，對那些分?jǐn)?shù)絕大部分集中在60分或者90分的情況進(jìn)行調(diào)整，使其成為分布合理、具有比較意義的分?jǐn)?shù)呢？這是許多教師迫切需要幫助解決的一個問題[8]。

二 《資源與環(huán)境材料學(xué)》課程考核成績修正

（一）課程特點

《資源與環(huán)境材料學(xué)》是資源循環(huán)科學(xué)與工程專業(yè)的重要必修課，也是與環(huán)境工程、材料科學(xué)與工程等專業(yè)課程聯(lián)系的橋梁。目前，國內(nèi)開設(shè)環(huán)境材料課程的學(xué)校較多，但每所學(xué)校特色不同，教學(xué)內(nèi)容的側(cè)重點也存在差異。我校具有悠久的冶金辦學(xué)特色，因此本課程側(cè)重于冶金固廢資源的綜合利用，教學(xué)內(nèi)容也引入了大量冶金固廢處理的實例，另外，在校內(nèi)未發(fā)現(xiàn)本課程或同類課程建成為精品課程，因此，作為固廢資源循環(huán)利用領(lǐng)域的重要理論課程，將本課程建設(shè)成為校級精品課程十分必要，不僅能促進(jìn)課程教學(xué)的發(fā)展，也可使學(xué)生更加重視和有效掌握本課程所覆蓋的知識點。隨著資源循環(huán)科學(xué)與工程本科專業(yè)培養(yǎng)目標(biāo)的明確和完善，由于該課程契合了專業(yè)培養(yǎng)目標(biāo)中能夠正確認(rèn)識資源循環(huán)過程對環(huán)境和社會的影響，熟悉環(huán)境保護(hù)和可持續(xù)發(fā)展的方針、政策等要求，重要性不斷凸顯，與其它專業(yè)課程相比，該課程具有鮮明的冶金資源特色，可為學(xué)生從事與資源循環(huán)利用、環(huán)境保護(hù)、生態(tài)設(shè)計等相關(guān)的生產(chǎn)、研發(fā)、經(jīng)營管理等工作提供理論知識的支撐。

（二）課程成績分布修正

傳統(tǒng)的課程考核以筆試為主，外加平時成績簡單相加。筆試主要考察學(xué)生的知識掌握情況，導(dǎo)致學(xué)生們形成死記硬背、臨時突擊等消極的應(yīng)試習(xí)慣[2]。平時成績則主要依賴于學(xué)生學(xué)習(xí)主動性與到課、與任課教師互動的積極性。導(dǎo)致學(xué)生課程考核成績評價不準(zhǔn)確，且不能有效反映任課教師教與學(xué)生學(xué)的效果，同時成績分布隨機(jī)性很大，往往很難符合正態(tài)分布。對于不是正態(tài)分布的課程成績需要進(jìn)行換算調(diào)整，以使其盡可能符合正態(tài)分布。現(xiàn)有的換算方法一般分兩種，一種是[9]根據(jù)偏度情況修正為對數(shù)正態(tài)分布，如果原數(shù)據(jù)呈現(xiàn)正偏態(tài)分布時，可以找到某一常數(shù)K，用K加上考分，再用對數(shù)變換后成為正態(tài)分布，就說明其服從對數(shù)正態(tài)分布；當(dāng)原數(shù)據(jù)成負(fù)偏態(tài)分布時，可以找到某一常數(shù)K，用K減去考分，再用對數(shù)變換法作描述統(tǒng)計，并檢驗其服從對數(shù)正態(tài)分布。另一種方法是基于給定的平均值和標(biāo)準(zhǔn)差構(gòu)造出正態(tài)分布曲線，并計算各個劃分上的期望頻數(shù)，然后根據(jù)各個期望頻數(shù)值，從原始分布中按照排名順序提出相應(yīng)數(shù)值，并按原始分布比例映射到相應(yīng)區(qū)間上[10]。但這些方法都比較復(fù)雜，實際換算比較困難，且并不能完全解決分?jǐn)?shù)扎推、不及格區(qū)間及優(yōu)秀區(qū)間的正態(tài)分布問題。

（三）修正算法

本文提出了一個被實踐證明更為簡便的修正算法，再配合使用Excel 2016軟件的簡易計算功能，使課程分?jǐn)?shù)能輕松換算成符合正態(tài)分布，且可以不考慮原始數(shù)據(jù)集是否符合正態(tài)分布。此修正方法根據(jù)給定的各分?jǐn)?shù)段比例，從原始分布中按排名順序提出相應(yīng)分?jǐn)?shù)，并按原始分布比例映射到相應(yīng)區(qū)間上。具體修正方法為：

首先設(shè)定學(xué)生課程分?jǐn)?shù)的全部數(shù)據(jù)樣本按從高到低為A(a1, a2, a3,……an)，修正后的課程分?jǐn)?shù)從高到低對應(yīng)為B(b1, b2, b3,……bn)。根據(jù)實際情況設(shè)定為優(yōu)秀[90 100]、良好[80 89]、中等[70 79]、及格[60 69]和不及格[0 59]五等；或者優(yōu)[90 100]、良[80 89]、中[60 79]和差[0 59]四等。同時根據(jù)需要設(shè)置各分?jǐn)?shù)段的比例，如優(yōu)秀：良好：中等：及格：不及格=10%：20%：40%：20%：10%；優(yōu)：良：中：差：=10%：40%：40%：10%。即樣本A的前面10%*n的數(shù)據(jù)為優(yōu)秀，相應(yīng)的后面的數(shù)據(jù)與級別相對應(yīng)。其他根據(jù)需要設(shè)成優(yōu)、良、中、差四種等級也是如此修正。

從最高分?jǐn)?shù)開始，調(diào)整各分?jǐn)?shù)段的分?jǐn)?shù)。若n=100，實際需要設(shè)定為優(yōu)秀、良好、中等、及格不及格五等，各段比例為10%、20%、40%、20%和10%。

計算結(jié)果四舍五入取整。

表1 五等設(shè)置課程分?jǐn)?shù)修正對比

（四）實例分析

現(xiàn)以我院《資源與環(huán)境材料學(xué)》的課程成績?yōu)槔瑢π拚惴ㄟM(jìn)行實例應(yīng)用。具體做法是，先在Excel 2016中將38位考生的卷面分?jǐn)?shù)按降序排列，分為五等修正；各分?jǐn)?shù)修正段占比人數(shù)為：優(yōu)秀與不及格設(shè)定為10%，38×10%=4人；良好與及格各20%，38×10%=8人，剩下14人為中等。然后在Excel 2016中各修正段分別按式(1)-(5)進(jìn)行簡單修正。修正前后成績?nèi)绫?所示。

圖1為五等設(shè)置修正前后分?jǐn)?shù)的分布直方圖。觀察直方圖可發(fā)現(xiàn)，通過利用Excel簡單的修正，不僅數(shù)據(jù)的頻數(shù)分布很好地滿足了正態(tài)分布的特征，且不及格率也控制在了合理水平以內(nèi)，不及格由28.9%修正為10.5%。

同樣以該門課程的成績?yōu)槔M(jìn)行“優(yōu)良中差”四等設(shè)置修正，修正結(jié)果分別表2和圖2所示。從圖2可以看出，經(jīng)過修正，差的比例由28.9%縮小至10.5%，良的比例由10.5%提高到39.5%，課程成績分布比較合理。

三 結(jié)語

考試是老師檢查學(xué)生學(xué)習(xí)效果以學(xué)習(xí)態(tài)度的重要手段，課程成績是學(xué)生評優(yōu)評獎的重要依據(jù)。考試和課程成績實際上已成為激勵學(xué)生努力學(xué)習(xí)的一個壓力泵、動力源。由于學(xué)生的天賦及自身的努力程度不一樣，所以即使教師的教學(xué)水平基本保持正常，學(xué)生對待學(xué)習(xí)的態(tài)度保持一致，期末課程成績的分布也不一定就是正態(tài)的。一旦出現(xiàn)非正態(tài)的成績，課程教師需要花費(fèi)大量心思在出題以及評卷上“下功夫”，而這種行為也會很大程度影響學(xué)生的努力程度，比如教師也為了考試成績的正態(tài)分布而采取如把題目難度下降等，這樣天賦高的努力程度高的學(xué)生與原本及格實力的學(xué)生在分?jǐn)?shù)上區(qū)分不大，都在中等的區(qū)間內(nèi)。這不利于激勵學(xué)生平時刻苦學(xué)習(xí)的積極性，也不利于促進(jìn)教學(xué)質(zhì)量的提高。

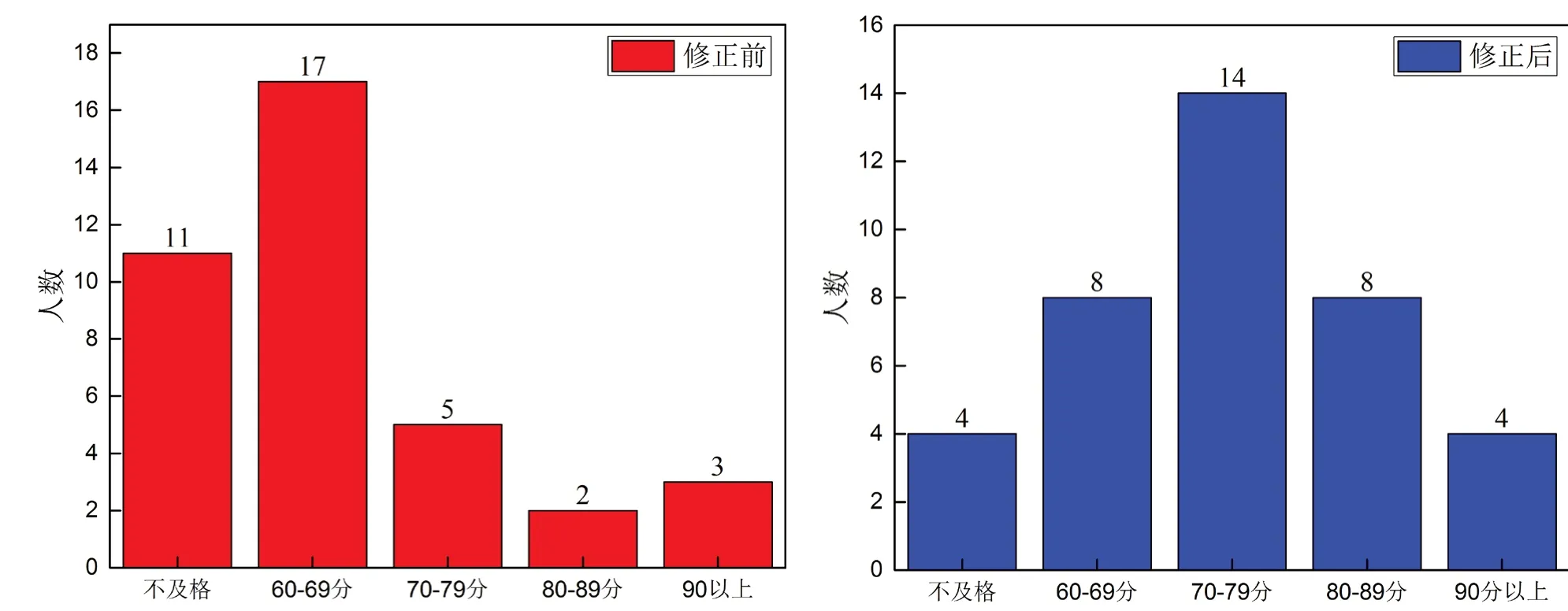
圖1 五等設(shè)置修正前后課程分?jǐn)?shù)分布圖

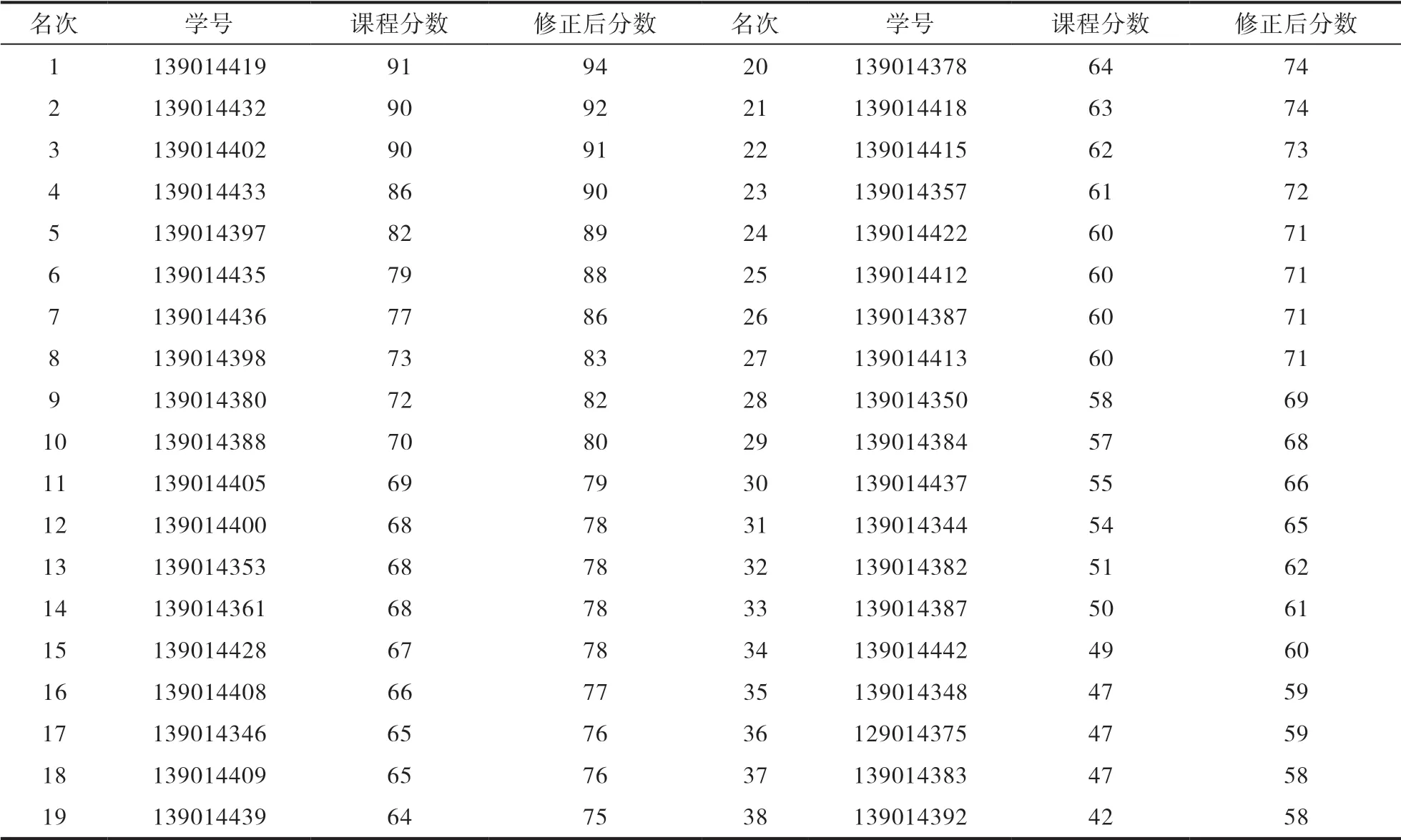
表2 四等設(shè)置課程分?jǐn)?shù)修正對比

本文提出了一種基于給定標(biāo)準(zhǔn)對非正態(tài)分布的數(shù)據(jù)進(jìn)行正態(tài)修正的算法，以某門不符合正態(tài)分布特征的課程成績?yōu)槔鶕?jù)兩種不同給定的各分?jǐn)?shù)段比例，用本文中的算法對課程成績進(jìn)行了修正，修正結(jié)果不僅沒有影響原先的排名順序，而且修正后的數(shù)據(jù)很好地符合了正態(tài)分布特性，同時控制了一定的不及格率，督促學(xué)生努力學(xué)習(xí)，避免成為最后幾名而不及格。我們希望我們提出的修正法，可以一定程度上使任課老師在學(xué)生課程成績不符合正態(tài)分布上節(jié)省精力投于科研和更好的教學(xué)，同時起到激勵學(xué)生努力學(xué)習(xí)、避免課程不及格。

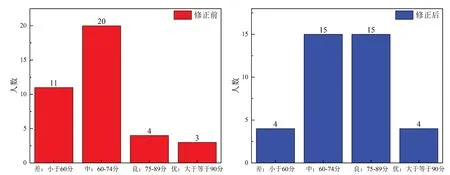
圖2 四等設(shè)置修正前后課程分?jǐn)?shù)分布圖