不同品種雞蛋貯期S-卵白蛋白含量分析及其可見/近紅外光譜無損檢測模型研究

付丹丹 王巧華 高升 馬美湖

摘?要?利用可見/近紅外光纖光譜采集羅曼粉殼和海藍褐殼兩個品種的雞蛋在349-1000 nm的透射光譜， 對270枚雞蛋的天然卵白蛋白的S-型空間構象異構體（S-卵白蛋白， S-ovalbumin， S-ova）含量進行了定量分析， 實現了不同品種雞蛋中S-卵白蛋白含量的快速無損檢測。通過比較貯期不同品種雞蛋的平均光譜發現， 兩個品種雞蛋的光譜吸收峰位置相同， 僅可見光范圍內的光譜吸收能量值有所不同。通過標準正態變量校正（SNV）對原始光譜進行預處理， 并利用無信息變量消除算法（UVE）從500～950 nm的全光譜中提取了67個特征波長， 建立的偏最小二乘（PLS）回歸模型可以很好地預測不同品種的S-卵白蛋白含量。為了更進一步消除特征波長之間的多重共線性， 利用逐步回歸（Stepwise regression）算法對特征波長進行二次篩選， 最終篩選出了16個特征波長， 建立多元回歸模型， 其校正集的決定系數（R2）為0.9511， 均方根誤差（RMSE）為0.0478， 預測集的R2為0.8380， RMSE為0.1116， 預測集相對分析誤差（RPD）為2.2620。 此模型對預測集中50個羅曼粉殼雞蛋和40個海藍褐殼雞蛋樣本的R2分別為0.8119和0.9116， RMSE分別為0.1298和0.0834， 模型適用性更佳。本研究結果表明， 可見/近紅外光譜能夠對不同品種的S-卵白蛋白含量進行無損檢測， 建立的通用預測模型為開發便攜式蛋白含量無損檢測裝置奠定了基礎。

關鍵詞?可見/近紅外光譜; 雞蛋; S-卵白蛋白; 相關性; 通用模型

1?引 言

雞蛋作為人們日常生活中重要食物之一， 其品質的評價和預測一直是食品加工等領域的研究熱點。卵白蛋白（Ovalbumin， Ova）是蛋清蛋白的主要成分， 占蛋清總蛋白的54%～63%， 卵白蛋白在貯存期間不可逆地轉化為一種熱穩定形式S-型空間構象異構體S-卵白蛋白（S-ovalbumin， S-ova）， 貯存期間蛋清中S-卵白蛋白相對全部卵白蛋白的質量分數由新產蛋的5%上升至冷藏6個月后的81%[1]， 且其形成不依賴于雞齡、營養狀況和蛋重等因素， 顯示出高的重復性與低的自然變異性， 轉化速率也僅受pH值和溫度的影響[2]。研究發現， S-卵白蛋白與貯存時間及雞蛋鮮度評價常用指標之間具有高度相關性[3]。因此與雞蛋品質密切相關的S-卵白蛋白被考慮作為評價商業雞蛋鮮度的參考指標。

目前， 檢測雞蛋S-卵白蛋白含量主要有3種方法。一是將蛋清稀釋后水浴加熱， 測定吸光度計算其含量[2]; 二是采用電化學傳感器， 如分子印跡技術對蛋清中S-卵白蛋白進行特定的分子識別， 繼而測定其含量[4]。這兩種方法均需把蛋打破， 經檢測才能準確判斷， 因此檢測周期長， 程序復雜， 且是破壞性檢測， 不能滿足快速檢測的要求。第三種方法利用光譜無損檢測技術， 如本研究組前期利采用高光譜成像技術， 利用已建立的模型對S-卵白蛋白含量進行檢測[5]， 但該研究只對海藍褐殼雞蛋進行了研究， 且預測模型的適用性還有待進一步的考察。

可見/近紅外光譜技術是一種成本低、速度快的無損檢測技術[6～8]， 已廣泛應用于雞蛋內部品質的在線檢測[9]和靜態檢測中。段宇飛等[10]建立了可見/近紅外光譜數據與雞蛋新鮮度之間的非線性回歸模型; Dong等[11]利用可見/近紅外光譜在雞蛋新鮮度預測的過程中比較了蛋白和整蛋的酸堿度; Syduzzaman等[12]使用600～900 nm波長范圍的光譜建立了蛋黃含量預測模型; Dong等[13]指出， 可見/近紅外透射光譜是檢測非受精蛋的有效手段。目前對雞蛋蛋白含量的無損檢測主要是通過氮元素的含量來測定整個蛋清中蛋白質的含量， 吳建虎等[14]基于可見/近紅外反射光譜技術， 利用多元散射校正預處理方法和多元回歸模型對新鮮蛋中的蛋白質含量進行了較好的預測。李海峰等[15]指出， 基于400～1000 nm波長范圍的光譜能夠對新鮮雞蛋的蛋白質含量進行較好的預測。但是目前還沒有利用可見/近紅外光譜對貯期的蛋白含量， 特別是對某一種特定的主要蛋白含量進行無損檢測的報道。 此外， 對蛋白含量的無損檢測都只是針對某一個品種， 其建立的模型適用性有限。

本研究采用可見/近紅外光譜分析技術， 應用無信息變量消除算法（Uninformative variables elimination， UVE）及逐步回歸（Stepwise regression）算法篩選出了S-卵白蛋白含量的特征波長， 并應用偏最小二乘回歸分析（Partial least squares， PLS）和多元線性回歸分析方法， 構建同時適用于兩個品種雞蛋S-卵白蛋白含量的無損預測模型。

2?實驗與方法

2.1?儀器與設備

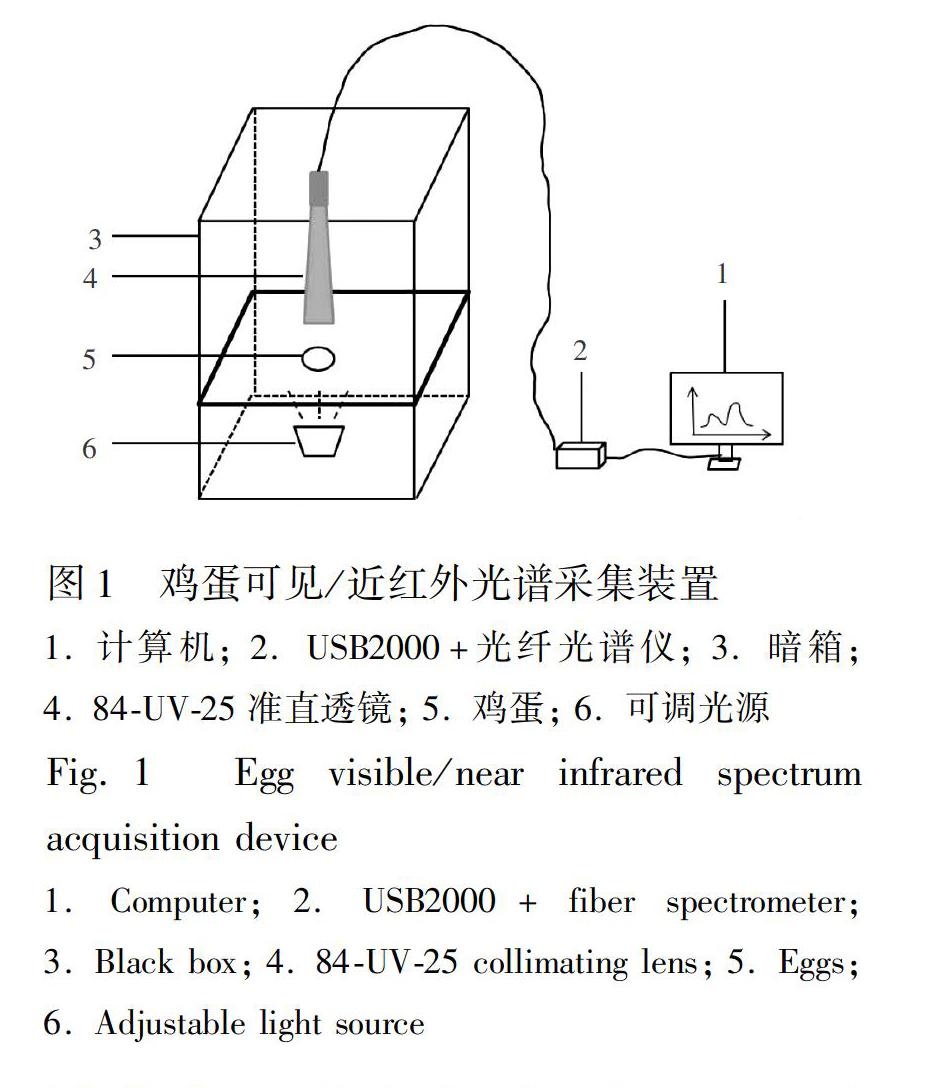
USB2000+可見/近紅外光纖光譜儀（美國Ocean Optics公司）; 電子天平、JA2002數顯游標卡尺（上海浦春計量儀器有限公司）; DU700紫外/可見光分光光度計（美國貝克曼庫爾特有限公司）。圖1為測定雞蛋的可見/近紅外光譜檢測系統示意圖。

2.2?實驗樣本和實驗方法

實驗樣品為某養雞場的當日產的兩個品種新鮮雞蛋， 共270枚， 所有雞蛋均無裂紋且干凈。其中海藍褐殼雞蛋和羅曼粉雞蛋各135枚， 均貯藏在恒溫恒濕培養箱中， 貯藏條件為22℃， 相對濕度為65%。每隔5天隨機取樣， 即貯藏第1、6、11、16、21、26、31、36和41天時， 隨機挑選出30枚雞蛋， 其中海藍褐殼雞蛋和羅曼粉殼雞蛋各15枚， 依次編號。

2.2.1?可見/近紅外光譜的采集?實驗采集每一枚雞蛋的可見/近紅外光譜。采集參數的設定分別為：為了避免采集到的光譜數據不失真， 積分時間設置為60 ms; 為了在保證在盡量短的時間內獲得更可靠的光譜數據， 平均掃描次數為3; 為了在避免較大的光譜噪音的同時不丟失光譜數據的細節特征， 平滑寬度設置為5; 光譜波段范圍為原始范圍， 即349～1000 nm， 光譜間隔為1 nm。每次實驗時， 將隨機挑選出來的雞蛋逐個放置， 以雞蛋的長軸與地面平行的方式每次放置一枚， 以保證在采集透射光譜的時候無漏光。

2.2.2?雞蛋新鮮度指標的測定?采集完光譜數據后， 用電子天平對每個雞蛋稱重后， 將雞蛋打破， 放置在玻璃平板上， 然后用游標卡尺測量3個不同位置的濃蛋白（新鮮雞蛋打破以后， 將其平攤放置， 有明顯的厚度那部分蛋清）高度、蛋黃直徑和蛋黃高度， 分別取其平均值作為最終每枚雞蛋濃蛋白高度值、蛋黃直徑值和蛋黃高度值。哈夫值（Haugh unit， HU）[16]是美國農業部蛋品標準規定的檢驗和表示雞蛋新鮮度的指標， 利用公式（1）求出。 蛋黃指數（Yolk index， YI）是蛋黃高度與蛋黃直徑的比值， 也可用于表示雞蛋的新鮮度， 可利用公式（2）求出。

HU=100lg（h+7.57-1.7m0.37）（1）

其中， m為蛋重（g）， h為濃蛋白高度（mm）。

YI=H/D（2）

其中，H為蛋黃高度（mm）; D為蛋黃直徑（mm）。

2.2.3?S-卵白蛋白含量的測定?將采集完光譜數據的雞蛋打破， 參照文獻[2]中的方法， 分別測定兩個品種雞蛋的S-卵白蛋白的含量。 首先分離蛋清的蛋黃， 每枚雞蛋分別取（5 ± 0.05）g蛋清液， 各加入25 mL磷酸鹽緩沖液（6.85 g NaH2PO4·2H2O與21.55 g Na2HPO4溶解于去離子水中， 定容至500 mL。每次實驗時稀釋20倍， 調至pH 7.5）; 經磁力攪拌后， 每個樣本各取兩份5 mL混合液， 其中一份于75℃水浴加熱30 min后冷卻， 另一份未加熱的樣本作為對照。分別向未加熱及加熱的兩份混合溶液中加入沉淀劑并離心， 上清液加入雙縮脲溶液混合液， 靜置。測定每個樣品在540 nm處的吸光度（OD）， 以2 mL去離子水與4 mL雙縮脲溶液混合液做對照。按照式（3）計算S-卵白蛋白含量（S-OC）[2]：

S-OC（%）=ODTOD0×100% （3）

其中， OD0為未加熱時樣品的吸光度， ODT為加熱后樣品的吸光度。

2.3?樣本劃分與光譜預處理

兩個品種雞蛋樣本均為135個， 將其合并后進行建模分析， 共270個樣本， 按照2∶1的原則利用基于聯合X-Y距離的樣本集劃分（Sample set partitioning based on joint X-Y distance， SPXY）方法將所有的樣本劃分為校正集和預測集。最終校正集樣本有180個， 其中，羅曼粉殼雞蛋85個， 海蘭褐殼雞蛋95個; 預測集樣本有90個， 其中， 羅曼粉殼雞蛋50個， 海蘭褐殼雞蛋40個。各樣本集的S-卵白蛋白含量描述性統計分析如表1所示。

由于光譜數據會受到儀器噪聲及隨機誤差等的影響， 進而影響建模的準確性和精度， 因此需要采取合適的光譜預處理方法提高預測模型的預測能力和穩健性。

2.4?特征波長的篩選

UVE是基于PLS回歸系數B的算法， 用于消除不提供信息的變量[17，18]。依據PLS的原理， 在利用光譜矩陣X和S-卵白蛋白含量矩陣進行建模時， 兩者之間存在關系Y=XB+e， 其中B是系數向量， e是誤差向量， UVE是把相同與自變量數的隨機變量矩陣加入到光譜矩陣中， 繼而通過交叉驗證建立PLS模型， 得到相應的系數矩陣、分析系數向量b的平均值和標準偏差的商t的可靠性。

t（i） =mean（bi）/sd（bi）（4）

式中， mean（b）是系數向量b的平均值， sd（b）是系數向量b的標準偏差， i是光譜矩陣中的第i列向量。依據t的絕對值大小確定是否把第i列變量用到隨后的PLS模型中。

逐步回歸法篩選特征波長是根據對回歸貢獻最大的解釋變量相應的回歸方程逐步地引入其它的解釋變量[19]， 經過逐步回歸篩選出來的特征波長重要且沒有嚴重的多重共線性。

2.5?模型的建立與評價

PLS在普通的多元回歸模型基礎上進行了優化[20]， PLS在建模時， 先分解自變量和因變量， 同時從兩類變量中提取成分， 然后按照相關性大小將提取的成分排列， 最后選擇能夠更好解釋整個系統的新主成分參與模型的建立[21]。由于在利用全波段建模時， 自變量數過多， 故選擇建立PLS模型， 比較原始光譜和各種光譜預處理方法的建模效果。

對于建立的模型， 通過比較決定系數（Coefficient of determination， R2）及均方根誤差（Root mean square error， RMSE）評價模型的預測性能， 其中， Rc2為校正集決定系數（Coefficient of determination of calibration set， Rc2）， RMSEC為校正集均方根誤差（Root mean square error of calibraiton set， RMSEC）， Rp2為預測集決定系數（Coefficient of determination of prediction set， Rp2）， RMSEP為校正集均方根誤差（Root mean square error of prediction set， RMSEP）， 同時，使用相對分析誤差（Residual predictive deviation， RPD）表征模型的預測能力[22]。各評價指標的相關計算公式如下：

R2=ni=1（yi-）2/ni=1（yi-）2（5）

RMSEC（RMSEP）=1nni=1（yi-）2（6）

RPD=SDRMSEP（7）

其中， yi和i分別為校正集或預測集中的第i個樣本的S-卵白蛋白含量實測值或預測值， 為對應校正集或預測集中總樣本的S-卵白蛋白含量平均值， SD為預測集樣本的S-卵白蛋白含量的標準差， n為校正集或預測集樣本總數。

相關系數越大， 均方根誤差越小， 模型的穩定性越高， 擬合程度越高， 模型預測性能越好。當RPD<1.5時， 模型無法對樣本進行預測， 1.52時， 模型能夠對樣本進行極好的預測。

3?結果與討論

3.1?不同品種雞蛋典型可見/近紅外光譜比較分析

分別對海藍褐殼雞蛋和羅曼粉殼雞蛋的典型可見/近紅外光譜進行對比分析， 對各品種的135個光譜數據取平均值， 將此平均光譜作為該品種雞蛋的典型光譜。如圖2所示， 通過對比可知， 兩種雞蛋在近紅外區域（780～950 nm）的光譜圖差異不明顯， 這可能是因為近紅外區域的光譜主要反映雞蛋內部化學結構信息，

研究表明， 蛋殼顏色及厚度對光譜吸收峰的能量值大小有影響[23]， 蛋殼越厚， 強度越大， 其整體結構致密， 乳突間隙小; 蛋殼顏色越深， 光吸收能力越強。粉殼雞蛋的殼較薄， 且殼色較淺， 因此相對褐殼雞蛋更易透光， 故粉殼雞蛋在可見光區域的典型光譜透射率明顯高于褐殼雞蛋。

因此， 盡管兩個品種的雞蛋的典型光譜存在差異性， 但是整體差異性較小， 且不同品種的S-卵白蛋白含量值顯著強相關， 因此可以直接將兩個品種合并， 建立通用的S-卵白蛋白含量無損檢測模型。

3.2?光譜預處理

分別利用Savitzky-Golay平滑（Savitzky-Golay smoothing， SG， 平滑窗口寬度為5）、一階微分（First ferivative， FD）、多元散射校正（Multivariate scattering correction， MSC）、標準正態變量校正（Standard normal variate， SNV）對原始光譜進行處理， 并分別建立PLS預測模型。由表3可知， 經過SNV預處理建立的PLS模型預測效果更好， 校正集和預測集的R2最高， 校正集RMSEP最低， 且RPD為1.9336。因此， 后續的數據處理均是基于經SNV預處理后的全光譜進行的。

3.3?特征波段篩選

將經過SNV處理過的全光譜作為PLS模型的輸入， 利用UVE算法進行波段篩選， 當PLS模型中包含的主成分變量設置為30時， 如圖3所示， 作為451個變量的穩定性t_value的分布圖， 右側為UVE隨機產生的451個變量的穩定性t_value的分布圖， 其中兩條水平的虛線是變量篩選的閾值上下限， 虛線以外的變量保留， 虛線以內的變量則全部消除。經過UVE變量篩選后得到67個波長， 這67個波長在光譜中的分布如圖4所示。

3.4?模型的建立與分析

基于UVE篩選出的67個波段建立PLS模型， 如表4所示， 校正集和預測集的R2分別為0.9591、0.8124， 預測集RPD為2.0911， 表明此模型能夠對S-卵白蛋白含量進行很好的預測。但是， 在建立PLS模型時， 根據PLS算法的原理， 最終只選取了15個主成分進行回歸計算。

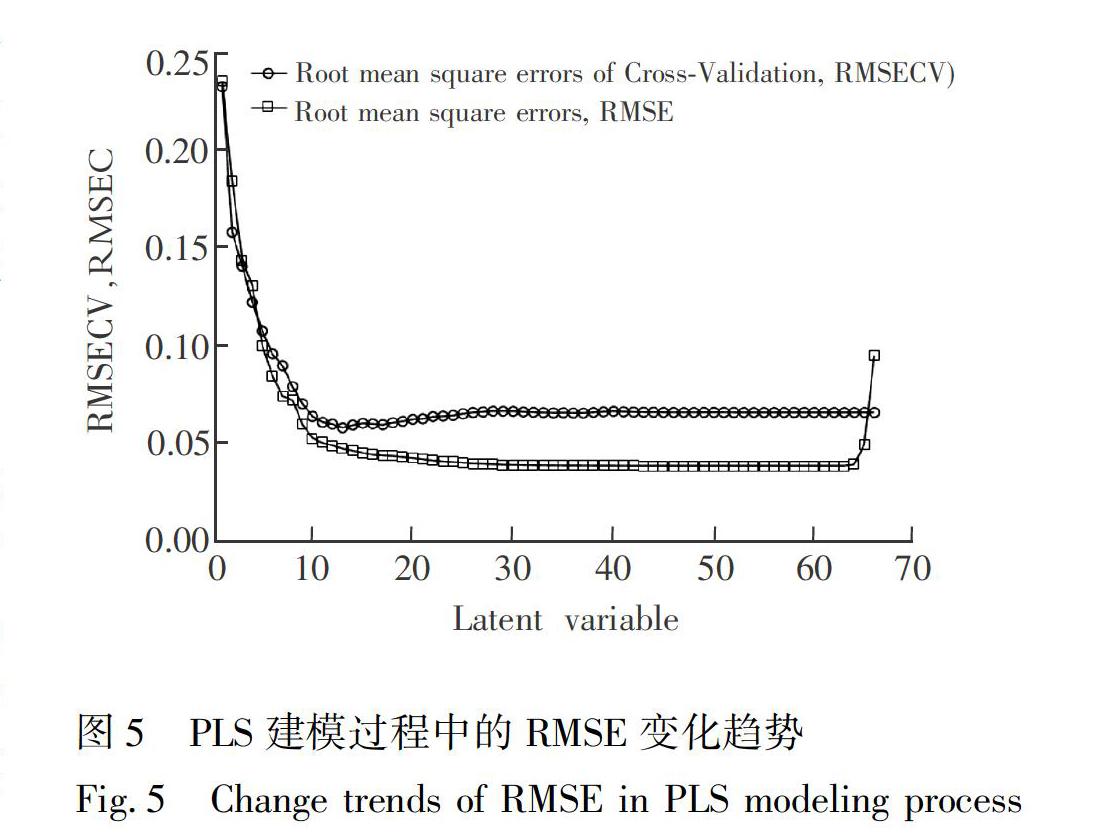
如圖5所示， 不論是否經過交叉驗證， 根據RMSE的變化趨勢， 都可以看出經UVE篩選出來的67個波段依然存在多重共線性的問題。這主要是由于在利用UVE篩選波段時， 有用波段信息和無用波段信息的判斷標準是基于PLS的回歸系數矩陣B設置的， 而回歸系數矩陣B直接受到PLS回歸中的主成分數影響。

根據UVE的算法原理， PLS回歸中的主成分個數是隨機設定的， 本研究篩選出的67個波段是在PLS回歸中主成分數為30的前提下， 當RMSECV最小且趨于穩定的情況下得出的， 因此無法完全保證篩選出的波段之間不存在共線性的關系。

3.5?二次波段篩選與建模

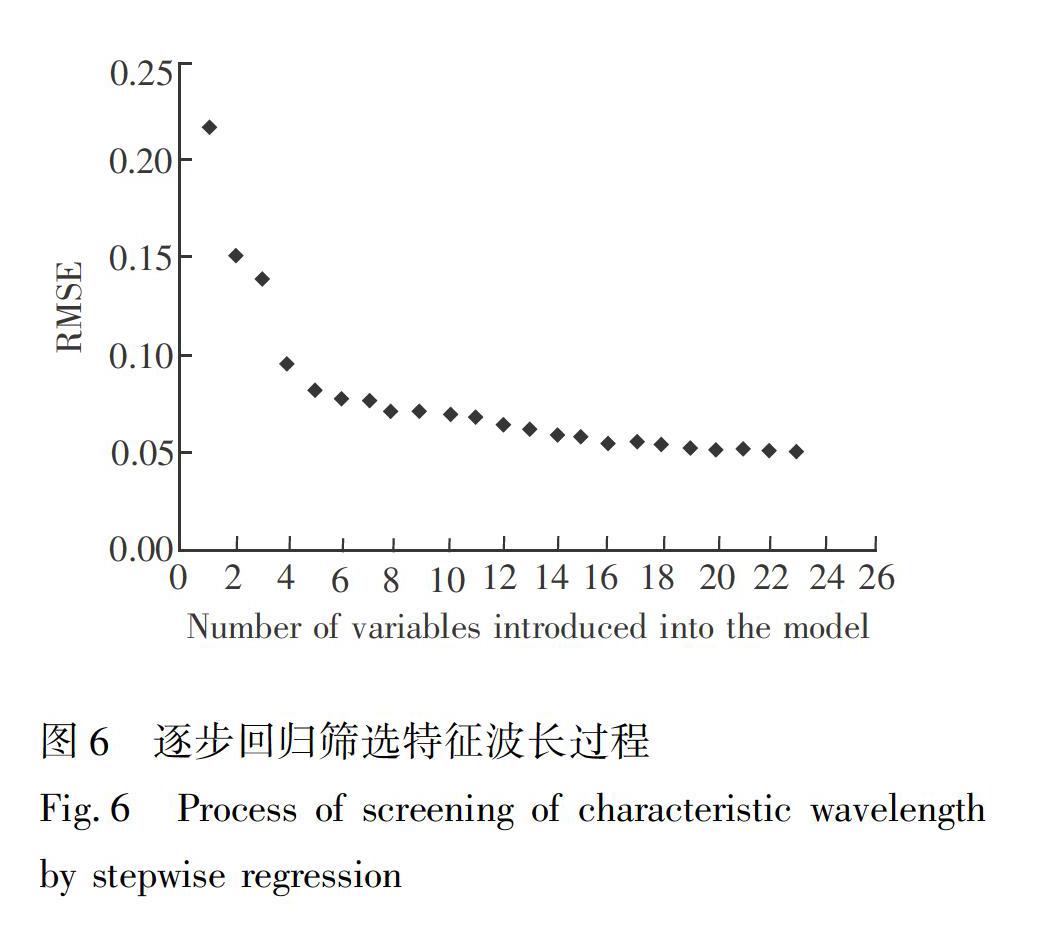
有研究表明， 二次波段篩選能夠進一步的簡化模型結構， 提高模型的預測性能[24]。為了進一步消除波段間的多重共線性， 使用逐步回歸對UVE篩選出的特征波段進行二次篩選。將經過UVE篩選出的67個波段作為多元回歸模型的輸入， 逐個引入到模型中。由圖6可見， 當引入16個變量到模型中后， RMSE達到最小并趨于穩定， 因此利用逐步回歸方法最終篩選出來的與S-卵白蛋白含量緊密相關的特征波長為16個。

篩選出的16個波長如表5所示。由表5可知， 有近一半的特征波段在可見光范圍內， 由于S-卵白蛋白含量與哈夫值高度相關， 而哈夫值在可見光范圍內的特征波長主要集中在640～730 nm范圍內[24]， 且兩個品種的主要光譜差異表現在可見光區域， 因此， 可見光范圍內的波段可能與雞蛋的新鮮程度信息及殼色和殼厚有關。另一半的特征波段在近紅外范圍內， 分布較為分散， 可能主要與蛋白質的化學結構， 如CH鍵、OH鍵等化學鍵信息相關。

利用二次篩選出的16個特征波段建立多元回歸模型（公式（6））， 模型的預測性能如表4所示， 校正集Rc2為0.9511， RMSEC為0.0478， Rp2為0.8380， RMSEP為0.1116。與UVE篩選出的波段建立的偏最小二乘回歸模型相比， 此模型的Rc2相近， Rp2有所增加， 且RPD的值增加到了2.2620， 大于2.0， 說明此模型可以對S-卵白蛋白含量進行極好的預測。故基于二次篩選的特征波段建立的回歸模型， 預測性能更好， 模型結構更簡單， 建模變量更少， 更適合S-卵白蛋白含量便攜式無損快速檢測軟件的開發于應用。

Y=0.3597band501-0.3942band517-0.8850band667+0.5121band669+1.2364band700-

1.7793band723+1.5312band763-0.7272band782-0.9101band795+1.2249band812-

李海峰， 房萌萌. 食品工業科技，2017， 38（20）： 286-289， 293

16?Suktanarak S， Teerachaichayut S. J. Food Engineer.， 2017， 215： 97-103.

17?WANG Zhuan-Wei， CHI Xi， GUO Wen-Chuan， ZHAO Chun-Jiang. Transactions of the Chinese Society for Agricultural Machinery， 2018， 49（05）： 355-361

王轉衛， 遲 茜， 郭文川， 趙春江. 農業機械學報， 2018， 49（05）： 355-361

18?LI Qian-Qian， TIAN Kuang-Da， LI Zu-Hong. Chinese J. Anal. Chem.， 2013， 41（6）： 917-921

李倩倩， 田曠達， 李祖紅. 分析化學， 2013， 41（6）： 917-921

19?TU Yu-Long， ZOU Bin， JIANG Xiao-Lu， TAO Chao， TANG Yu-Qi， FENG Wei-Wei. Spectroscopy and Spectral Analysis， 2018， 38（2）： 575-581

涂宇龍， 鄒 濱， 姜曉璐， 陶 超， 湯玉奇， 馮徽徽. 光譜學與光譜分析， 2018， 38（2）： 575-581

20?Feng C H， Makino Y， Yoshimura M， Francisco J. Rodríguez P. Food Chem.， 2018， 264： 419-426

21?XIE Yue， ZHOU Cheng， TU Cong， ZHANG Zu-Liang， WANG Jian-Fei. Chinese J. Anal. Chem.， 2017， 45（3）： 363-368

謝 越， 周 成， 涂 從， 張祖亮， 汪建飛. 分析化學， 2017， 45（3）： 363-368

22?Qi H J， Tarin P K， Arnon K， Jin X， Li S W. Soil Tillage Res.， 2018， 175： 267-275

23?XIONG Huan， XU Hui-Rong， ZHOU Wan-Huai. Transactions of the Chinese Society of Agricultural Engineering， 2013， 29（Supp.1）： 264-269

熊 歡， 徐惠榮， 周萬懷. 農業工程學報， 2013， 29（Supp.1）： 264-269

24?FU Dan-Dan， WANG Qiao-Hua. Food Science， 2016， 37（22）： 173-179

付丹丹， 王巧華. 食品科學， 2016，37（22）： 173-179

Analysis of S-Ovalbumin Content of Different Varieties

of Eggs during Storage and Its Nondestructive

Testing Model by Visible-Near Infrared Spectroscopy

FU Dan-Dan1， WANG Qiao-Hua*1，2，3， GAO Sheng1， MA Mei-Hu2，4

1（College of Engineering， Huazhong Agricultural University， Wuhan 430070， China）

2（National Research and Development Center for Egg Processing， Huazhong Agricultural University， Wuhan 430070， China）

3（Ministry of Agriculture Key Laboratory of Agricultural Equipment in the Middle and

Lower Reaches of the Yangtze River， Wuhan 430070， China）

4（College of Food Science and Technology， Huazhong Agricultural University， Wuhan 430070， China）

Abstract?The visible-near-infrared （Vis-NIR） transmission spectroscopy technique was used to analyze the content of S-ovalbumin （S-ova）， which had high correlation with egg freshness， and to establish a nondestructive prediction model. The visible/near-infrared fiber spectroscopy were used to collect the transmission spectrum of two varieties of eggs at 349-1000 nm， and the S-ovalbumin content of 270 eggs was measured by wet chemistry method. By comparing the average spectra of eggs of different varieties during storage， it was found that the spectral absorption peaks of different varieties of eggs had the same position， and only the spectral energy values in the visible range differed. The original spectrum was preprocessed by standard normal variate （SNV）， and 67 characteristic wavelengths were extracted from the full spectrum of 500-950 nm using uninformative variables elimination （UVE）. It was concluded that partial least squares （PLS） regression model based on 67 characteristic wavelengths could predict the S-ovalbumin content. To further eliminate the multi-collinearity between the characteristic wavelengths， the stepwise regression algorithm was used to perform secondary screening on the characteristic wavelengths， and finally 16 characteristic wavelengths were selected. By using the 16 characteristic wavelengths to establish a multivariate regression model， the coefficient of determination （R2） of the training set was 0.9511， the root mean square error （RMSE） was 0.0478， and the R2 of the prediction set was 0.8380. Besides， the RMSE was 0.1116， and the residual predictive deviation （RPD） was 2.2620. The general predictive model was used to predict the S-ovalbumin content of 50 eggs with Roman pink shell and 40 eggs with sea blue brown shell in the prediction set. The R2 of the predicted and measured values were 0.8119 and 0.9116， respectively， and the RMSEs were 0.1298 and 0.0834， respectively. Therefore， the general model could perform nondestructive testing on the S-ovalbumin content of these two different varieties of eggs better， and the model was more applicable. The results showed that the visible/near-infrared spectroscopy could accurately detect the S-ovalbumin content of eggs in different varieties， and the established general prediction model laid a foundation for the development of portable non-destructive testing device for protein content.

Keywords?Visible-near infrared spectroscopy; Egg; S-Ovalbumin; Correlation; General model

（Received 11 June 2019; accepted 5 December 2019）

This work was supported by the National Natural Science Foundation of China （No.31871863）， the National Science and Technology Major Project of the Ministry of Science and Technology of China during the 12th Five-year Plan Period （No.2015BAD19B05） and the Special Scientific Research Fund of Agricultural Public Welfare Profession Project of China （No.201303084）.