淺析開放性數學問題的設計
陳 璽
(甘肅省隴南市成縣城關中學 742500)
開放性數學問題的出現以及在近二十年來迅速普及,已被人們認為是最富有教育價值的一種數學題型.開放性數學問題的教學能真正地達到“教學是師生經驗的展現與交流對話;教師是學生學習的合作者、促進者、組織者及引導者”,本能地體現師生互動.同時,教學還能給學生更多自主思考的空間,讓學生多一份感悟,多一份理解,并提供更多的創新、發現新知識的機會.
開放性數學問題是相對于傳統的封閉問題而言的,是指構成問題的背境材料、結論、解題依據和解題方法四個要素中缺少某些要素的命題.若缺少的要素是假設,則為條件型開放題;若缺少的要素是判斷,則為結論型開放題;若缺少的要素是推理或解法等,則為策略型開放題.有的問題只給出一定的情境,其條件、解題策略與結論都要求主體在情境中自行設定與尋找,多方面、多角度、多層次地探索,則稱為綜合型開放題.
例1為使下列各式可以因式分解(在整數范圍內),a,p分別可以取哪些整數?
(1)x2+ax-18;(2)x2+7x+p.
分析第(1)小題中a的確定與-18的因數有關.
-18=1×(-18)=(-1)×18 =2×(-9)=(-2)×9 =3×(-6)=(-3)×6.
得到a可以取6種不同的數值,即±17,土7,±3.
第(2)小題中p的確定與7是哪兩個整數的和有關.
7=3+4=2+5=1+6=0+7=(-1)+8=(-2)+9=(-3)+10=…, 所以p可以取無窮多個整數值,如12,10,6,0,-8,-18,-30等等.
由上例可知,在講十字相乘法(新教材已刪除)時可歸納:
(1)p是已知整數,對x2+ax+p進行分解時,因p的質因數有限,故a也有限;(2)a是已知整數,對x2+ax+p進行分解時,因a表示為兩個整數的和的方法數是無窮的,故p也是無窮的.
仿照此類型,可設計出很多開放問題,旨在培養學生思維的靈活性和深刻性.
例2如圖,在圓內接四邊形ABCD中,AC=BD,AC、BD相交于P,根據這些條件,你能得出哪些結論?
解根據在同圓中等弧、等弦及圓內接四邊形的有關性質及三角形全等或相似等性質,立即可得:
(1)弧AC=弧BD,弧AD=弧BC;(2)△APD≌△BPC;(3)DC∥AB,△PCD∽△PAB;(4)四邊形ABCD是等腰梯形;(5)∠ADC+∠ABC=180°,∠DCB+∠DAB=180°.
例3今有一正方形土地,要在其上修筑兩條筆直的道路,并把這塊土地分成形狀相同且面積相等的四部分.若道路的寬度忽略不計,請設計三種不同的修筑方案.(山東省中考題)
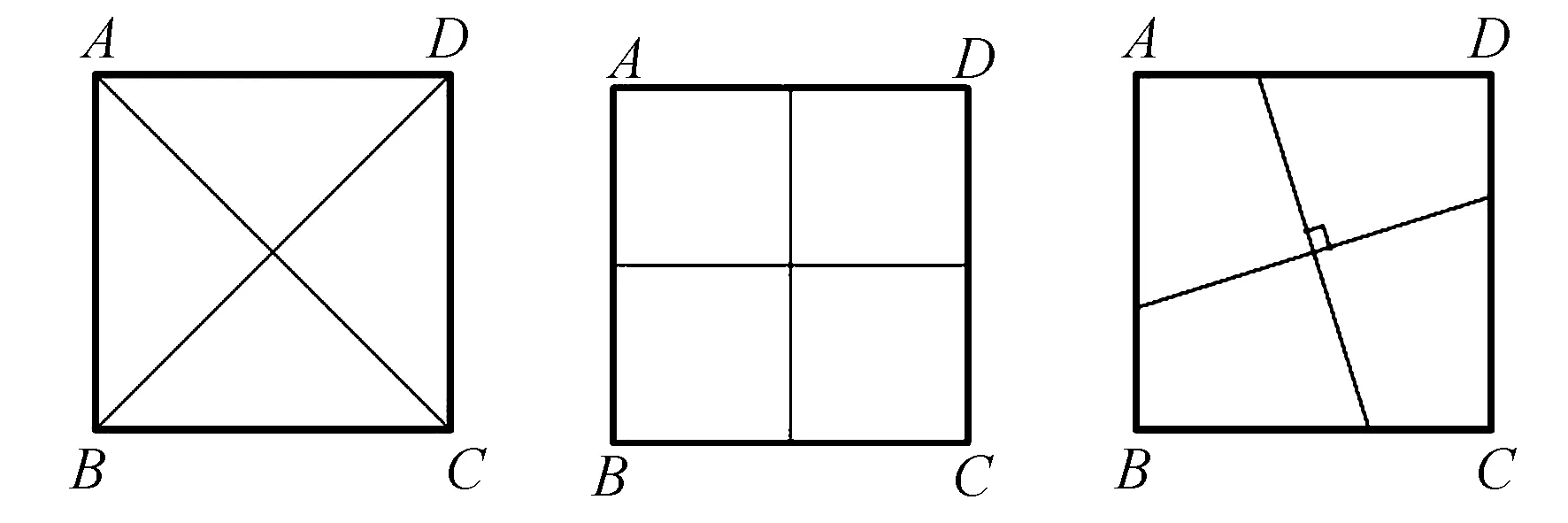
解(1)連結兩條對角線;(2)連結兩組對邊中點;(3)過正方形對稱中心任意作兩條互相垂直的直線.
分析這是一道策略開放題,(1)、(2)最易想到,(3)是創新畫法,顯然(1)、(2)是(3)的特殊情況.
如將本題“大小相等”去掉,設計的方案是極多的.
例4如圖,當△ABC≌△ADC時,顯然有∠BAC=∠DAC,AB=AD,BC=DC.
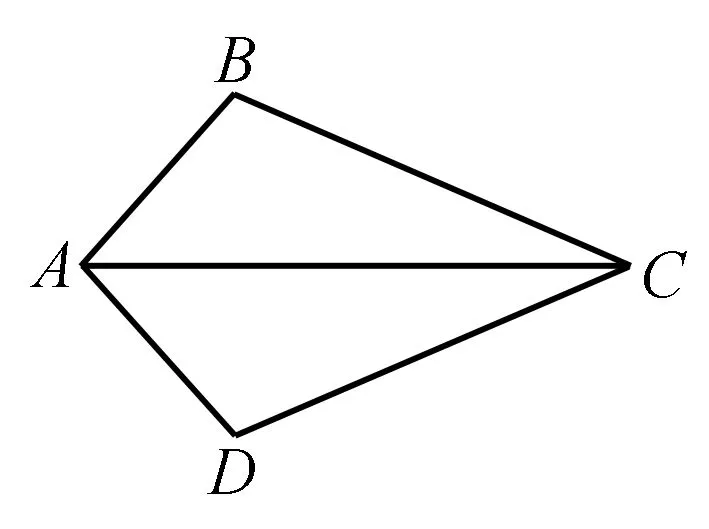
問題設計:在△ABC和△ADC中,有下列三個論斷:
①AB=AD;②∠BAC=∠DAC;③BC=DC.
以其中兩個論斷作為條件,余下一個論斷作為結論,寫出你認為正確的一個命題:____.(陜西西安市中考題)
分析此題基本上是將例4中的條件與結論對調,進行設計的條件及結論均開放的題目,要求具有較高的分析能力.
三個論斷中任何兩個都可以作為條件,剩余一個論斷則是結論,顯然,可構造出3個命題:①、②?③;②、③?①;①、③?②.
其中2個是正確的,1個是錯誤的.考慮到“SSA”不能判定全等,故正確的命題是①、②?③或①、③?②.
由以上可看出,開放性數學問題的設計,必須在嚴格的邏輯性前提下,或是將原題條件抽象化,變通相應字母或項;或是在原題設上進行引伸;或是在原題結論上拓廣;或是將題設部分與結論互調等等.既要對開放性問題進行“開放度”的把握和引導,又要對封閉題進行改造,讓它適度開放.“開放”多少,“開放”多深,還要看學生的知識基礎思維能力以及教材的內容等.
因此,教師在數學教學過程中,精心設計,合理、恰當地引進開放式教學,能充分體現學生的主體地位,學生的思維被全面激活,學生的概括能力和遷移能力得到提高,更好地反映學生的高層次思維,從而更有效地培養學生的邏輯思維能力和創新思維能力.同時,開放性數學問題的設計對教師的業務能力、 綜合素質也是一個極大的挑戰.

