基于初始條件優化的GM(1，1)冪模型及其應用

丁 松，李若瑾，黨耀國

(1.浙江財經大學經濟學院,浙江 杭州 310018; 2.浙江省之江青年區域經濟與統籌發展研究中心, 浙江 杭州 310018；3.南京航空航天大學經濟與管理學院,江蘇 南京 211106)

1 引言

灰色預測理論以其在對“貧信息、小樣本”特征數據建模擁有獨特優勢而受到眾多學者的關注。GM(1,1)模型和灰色Verhulst模型是灰色預測模型體系中比較重要的兩類模型，學者從背景值[1-2]、灰導數[3-4]、參數優化[5-6]、模型外推[7-8]等方面對兩類模型進行了一定的優化與拓展，進一步提升了模型的建模效果和應用領域。一般情況下，這兩種模型適用于近似灰指數率和灰飽和率的單調小樣本序列建模，對于波動性較強序列則束手無策。

GM(1,1)冪模型是GM(1,1)模型和灰色Verhulst模型的延伸，因其冪指數的不確定，可以根據建模數據的特點，如飽和序列、波動序列、高速增長序列等等，借助一定的技術手段，對冪指數進行優化求解，進而對多種特征序列具有很好的適應性和建模有效性，因此在經濟社會中得到較廣泛應用。鄧聚龍教授[9]首次提出GM(1,1)冪模型，但沒有給出冪指數的求解方法；王正新等[10]針對冪指數求解問題，借助灰色系統信息覆蓋原理首次給出了其求解路徑，并討論了不同冪指數對應模型的極限性質；李軍亮等[11]在分析冪模型建立機理基礎上，分析了曲線圖形與冪指數及發展系數間的關系，利用粒子群算法解出冪指數，取得較好的建模效果。丁松等[12]提出多變量離散灰色冪模型，并給出其參數估計方法和構造驅動控制的灰色冪模型。Hsu[13]分別利用遺傳算法優化冪模型的冪指數，并將其應用到電力載荷和集成電路產業預測中，取得了較好的預測效果。楊保華和趙金帥[14]提出了能夠表現指數型發展系統和冪函數型發展系統間相互作用關系的離散灰色冪模型，利用參數間的約束關系，構建了離散灰色冪模型初始條件的優化模型，并在中國網絡購物人數數據預測中取得較好的應用效果。王俊芳和羅黨[15]提出了一種新的分數階離散GM(1,1)冪模型，借助正則化算法求解參數以消除模型可能存在的病態性問題。為了改善GM(1,1)冪模型的建模精度，王正新、黨耀國等還分別從冪模型的無偏性[16]、病態性[17]、自記憶性[18]、時變參數[19]等角度進行了一定的拓展研究，并且在實踐應用中獲得了眾多學者的認可。

上述對GM(1,1)冪模型的改進均是從灰色微分方程的角度加以優化，在一定程度上提升了模型的建模精度，但對于灰色模型求解，初始條件的選取也是影響模型精度的關鍵因素之一。縱觀以往文獻的研究可以發現，對于GM(1,1)冪模型初始條件的優化研究主要分為三類，第一類：在以第一個分量x(1)(1)作為模型的初始條件[9]，該方法是傳統冪模型的初始條件選擇，應用較廣泛，其不足主要是選擇距離系統趨勢較遠的初始序列，沒有考慮新信息的作用，對于系統未來發展預測可能會存在一定偏差；第二類：Dang Yaoguo等[20]基于“新信息優先原理”，以第n個分量x(1)(n)作為初始條件，一定程度上改善了預測效果，但過度強調新信息對模型建模的影響，忽略舊數據對系統趨勢的修正作用；第三類：王正新等[21]以x(1)(1)和x(1)(n)線性組合，作為初始條件，通過構建非線性約束模型對最優組合權重進行求解。該方法一定程度上利用了最舊信息和最新信息，但其對于中間部分的有效信息沒有充分利用，對于已經是“少數據、貧信息”的灰色系統建模，勢必會對有效信息未能充分提取，造成信息浪費，從而影響灰色建模效果。

因此，本文將在上述研究的基礎上，對GM(1,1)冪模型的初始條件進行優化，充分利用舊數據的經驗知識和新數據的趨勢信息，綜合考慮新舊信息間的權重分配關系，實現初始條件最優化。在此基礎上，以相對誤差絕對值和為目標函數，構建初始條件和冪指數協同優化的GM(1,1)冪模型，利用智能算法或軟件進行參數優化求解。最后通過對我國網絡購物用戶規模預測的案例，對比GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))、GPM(1,1,β)和PIGPM(1，1,γ)四種模型的優劣。

2 GM(1，1)冪模型及其參數求解

2.1 GM(1，1)冪模型的三種基本形式

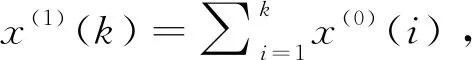
定義1對X(0)，X(1)，Z(1)的定義如上所述，則稱灰色微分方程：

x(0)(k)+az(1)(k)=b(z(1)(k))γ,γ≠1

(1)

為GM(1,1)冪模型。

定義2設a為發展系數，b為灰作用量，則稱

(2)

GM(1,1)冪模型的白化微分方程。

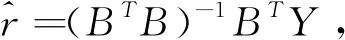
證明：略

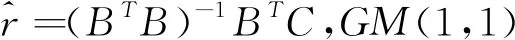
(1)白化方程的時間響應函數表達式為:

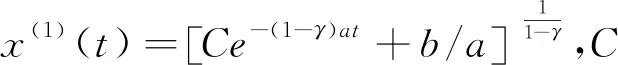
(3)在初始條件x(1)(t)|t=1=x(1)(1)時的時間響應式為：

(4)

(3)在初始條件x(1)(t)|t=n=x(1)(n)時的時間響應式為：

(5)

(4)在初始條件x(1)(t)|t=β=βx(1)(1)+(1-β)x(1)(n)時的時間響應式為[21]：

(6)

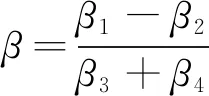
-b/a)e-(1-γ)ak

β4

(5)當k=2,3,…,n時，還原值為

(7)

證明：略

上述為傳統GM(1,1)冪模型的建模機理，冪指數γ是未知的，這就使得GM(1,1)冪模型有很大的靈活性去適應高速增長(或遞減)、飽和增長(或遞減)、波動震蕩等多種特征序列。目前，對于冪指數γ求解主要采用兩種方法：(1)利用灰色系統信息覆蓋思想[10]，借助一階和二階灰導數特性對冪指數進行求解，但該方法未以提升模型精度為依據，因此未必能獲得較好的精度；(2)借助非線性無約束優化模型，利用LINGO、MATLAB等軟件或者智能算法(粒子群、遺傳算法等)，實現對冪指數的最優化求解[11]。該方法以平均相對誤差最小化為目標，實現建模過程和模型檢驗標準相一致。定理2中分別給出了目前最常用的三個初始條件下GM(1,1)冪模型的表達式，分別記為GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))和GPM(1,1,β)。

2.2 GM(1，1)冪模型的的冪指數優化

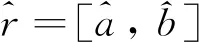
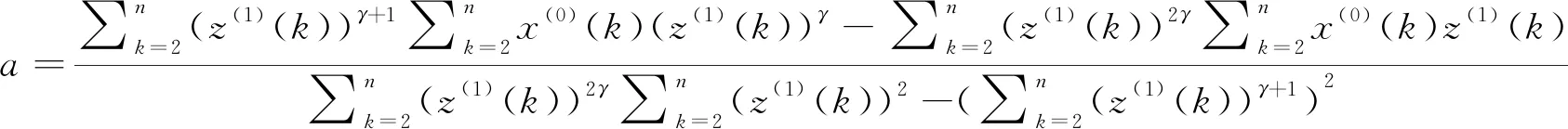
(8)

(9)

為了保證參數優化的目標函數與模擬預測結果檢驗準則統一，本文以平均相對誤差最小化為目標，將冪指數γ與系統參數a和b之間的關系作為約束條件，建立式(10)的非線性優化模型：

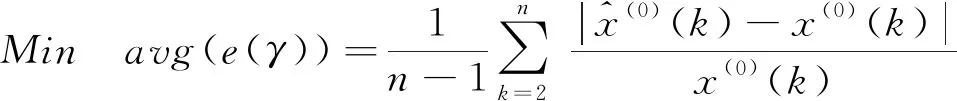
(10)

通過式(10)求解出冪指數參數后，再代入定理1求出系統參數a和b，進而利用定理2進行模擬和預測，實現冪指數最優化的GM(1,1)冪模型構建與應用，記冪指數優化GM(1,1)冪模型為GPM(1，1,γ)。

3 優化的GM(1，1)冪模型構建及參數求解

通過研究眾多文獻發現，初始條件的選擇對于灰色預測模型的精度有著重要的影響，在這部分，將提出GM(1,1)冪模型初始條件的新表達方式，并討論對初始條件及與冪指數γ的協同優化方法，然后研究時間參數的求解路徑。

3.1 GM(1，1)冪模型初始條件優化

實際建模過程中，GM(1,1)冪模型的模擬預測值不僅與第一個分量x(1)(1)或者第n個分量x(1)(n)有關，其應該與X(1)的每個分量都有著密切關系。根據新信息優先原理，新信息中包含了大量系統趨勢變化信息，對系統未來發展的認知作用大于舊信息，因而在建模時應賦予新信息較大的權重比例。與此同時，雖然舊信息的有效性在逐漸下降，對未來系統行為的預測作用在減弱，但也不能完全擯棄，舊信息中還存在部分價值數據，具有一定的經驗指導作用。因此，如何根據數據序列的實際意義處理新信息與舊信息間的權重分配問題以較為真實地反映權重信息在初始條件構建中的變化規律，是提高灰色建模功效的關鍵。為了充分考慮新舊信息對預測模型的影響，本文引入權重系數λn-k(0<λ<1)，k=1,2,…,n，以X(1)的每個分量的加權和作為初始條件對GM(1,1)冪模型進行優化，即以

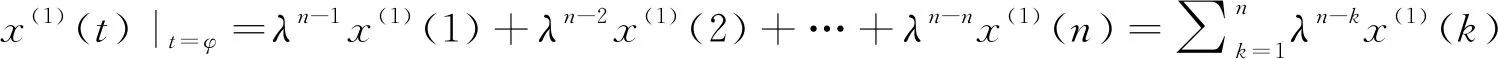
(11)

為初始條件。權重系數λn-k(0<λ<1),k=1,2,…,n隨著時間由遠及近呈現遞減趨勢，并且其遞減速率與λ取值相關，取值越大，遞減越慢，反之越快，如示意圖1所示，該圖中取k分別取1-10，在λ的不同取值下，權重系數的變化情況描述。該系數一定程度上揭示了一階累加序列的各分量作用隨著時間的往后推移在不斷變化，比較貼近實際。權重系數的選擇主要與數據序列在現實意義下的遞減規律所決定，不是人為設定。從圖1中可以看出，X(1)的各個分量的權重滿足λk-1<λk-2<…<λk-n，即新信息的權重大于舊信息的權重，并且各分量的作用均被考慮到，既滿足新信息優先原理，又充分利用各分量信息。

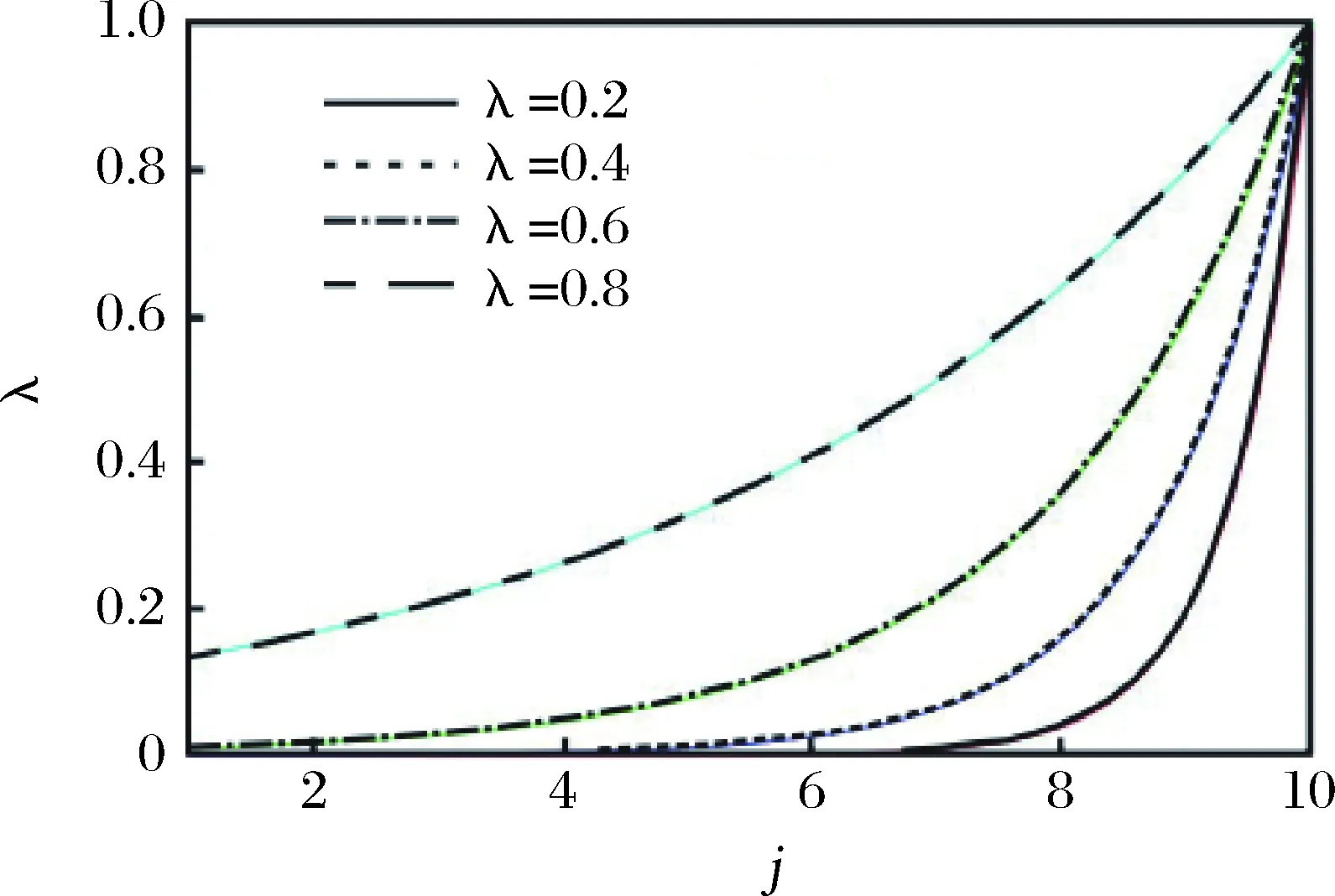
圖1 不同λ對應其權重系數遞減速率變化

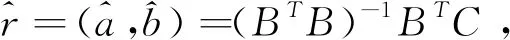
(12)

(2)還原值為

(13)

離散化可得時間響應式為

定理得證。

上述模型稱為全信息初始條件優化的GM(1,1)冪模型，記為PIGPM(1，1)( Grey Power Model Based on Perfect Information).該模型能夠更好的體現“新信息優先”和“信息充分利用”原理，綜合考慮各個變量的變化規律，并將其引入到模型初始條件中，克服了GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))和GPM(1,1,β)的缺陷：分別為對新信息利用不足，過分重視新信息，忽視中間信息的作用。另外，鑒于GM(1,1)模型和灰色Verhulst模型是GM(1,1)冪模型的特殊形式，對于GM(1,1)模型和灰色Verhulst模型也可以采取上述初始條件優化方法，可以進一步提升兩種模型的建模精度。

3.2 GM(1，1)冪模型的初始條件與冪指數協同優化建模

通過上述對GM(1,1)冪模型的初始條件優化，我們可以結合冪指數的優化方法，對初始條件參數φ和冪指數γ一并建立優化模型，進而實現初始條件和冪指數的最優解，進一步提升GM(1,1)冪模型的精度。

(14)

通過經典處理軟件(LINGO、MATLAB、EXCEL等)或者智能優化算法(粒子群、遺傳算法等)可以很方便的對上述模型進行求解，得到GM(1,1)冪模型的模型參數φ,γ,a和b，稱初始條件和冪指數協同優化的GM(1,1)冪模型為PIGPM(1，1,γ)。

4 實例分析

目前，中國經濟發展已經迎來“中高速增長”的新常態，進入深層次調整期，其關鍵就是新經濟增長點的不斷涌現和舊增長點的逐漸淡出。在我國經濟增長的“三駕馬車”中，消費已經超過投資，成為中國經濟增長的第一動力，中國經濟的“頂梁柱”。國家統計局數據顯示，2015年我國社會消費品零售總額30.1萬億元，同比增長10.7%，消費對GDP的貢獻率從2011年的51.6%升至2015年的66.4%。與此同時，傳統線下零售業迎來比以往更大的挑戰，自2012年以來出現增速連續四年下降，而網絡消費卻爆發出強勁增長動力，尤其是手機網絡購物發展勢頭迅猛，成為引領消費市場的新增長點。2015年全國網絡零售交易額達到3.88萬億元，同比增長33.3%，占全社會消費品零售總額比重持續增長至12.9%。截至 2015 年 12 月，我國網絡購物用戶規模達到 4.13 億，較 2014 年底增加 5183 萬，增長率為 14.3%，高于 6.1%的網民增速。網購用戶規模的快速擴張，網購群體主流年齡跨度增大，有向全民擴散的趨勢，為我國網絡消費市場的高速發展奠定良好的用戶基礎，釋放著巨大的市場潛力。

隨著當下我國“互聯網+”、“一帶一路”以及一系列有利于促進和保障我國網絡購物市場健康穩定發展的戰略、政策的出臺，我國網購市場的發展遠未飽和，市場前景廣闊。根據中國互聯網絡信息中心(CNNIC)發布的2013-2015年《中國網絡購物市場研究報告》，本文列出了2006-2015年我國網絡購物用戶規模的數據，見圖2。由圖可見，我國網絡購物用戶規模呈現快速發展的趨勢，網購用戶占網絡用戶比重不斷上升，從近三年看，網購用戶規模增速已經出現減緩勢頭，整體具有一定的飽和性，即S型增長。因此本文提出的冪指數模型能夠較好的描述網購用戶規模的發展規律，進而為未來用戶增長預測提供一種有效的工具。

在建模數據選擇上，本文以2006-2012年我國網絡購物人數為建模數據，2013-2015年為預測對比數據，數據見圖2。在模型的選擇方面，本文選取目前常見的三種初始條件優化的GM(1,1)冪模型和本文提出的基于全信息初始條件優化的GM(1,1)冪模型，分別記為：GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))、GPM(1,1,β)和PIGPM(1，1,γ)。

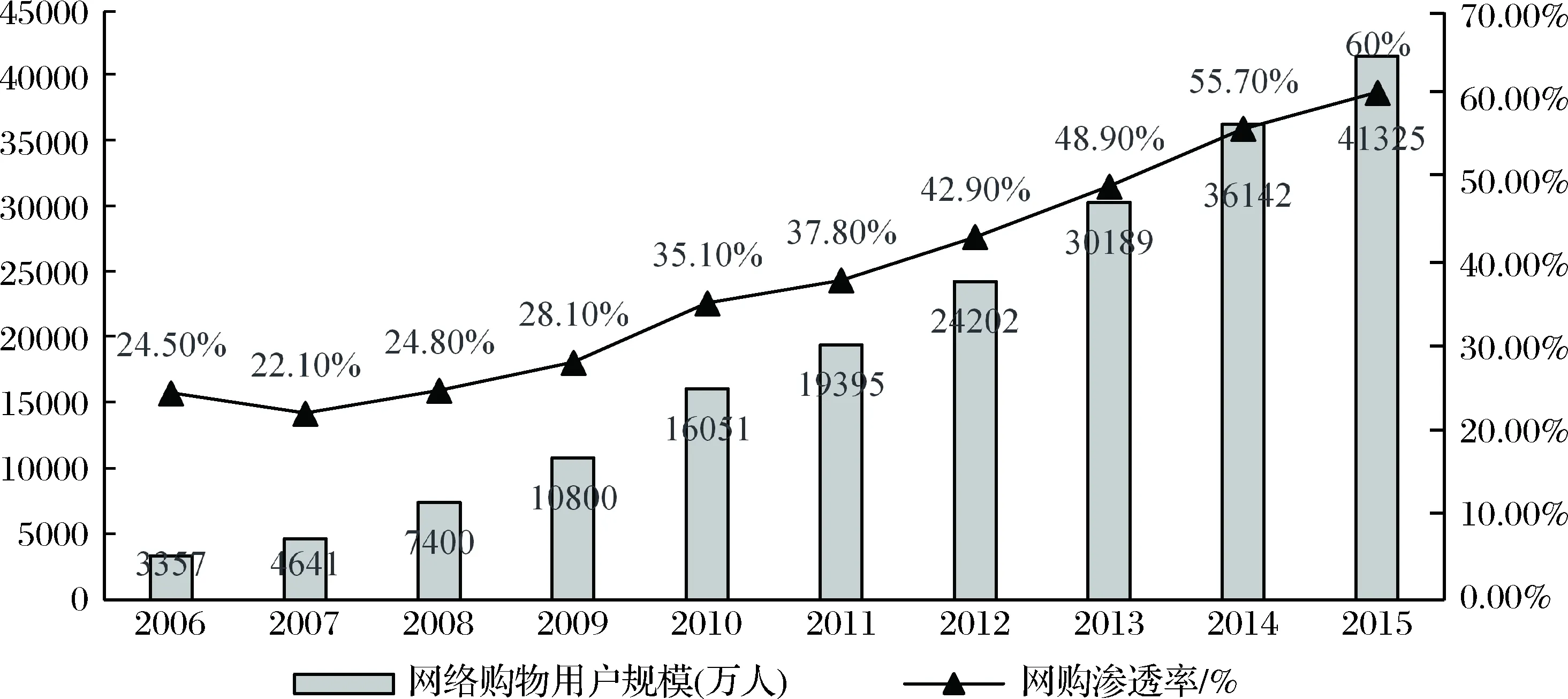
圖2 2006-2015年網絡購物用戶規模及滲透率

根據定理2中三種初始條件優化的GM(1,1)冪模型的計算公式可得：

GPM(1,1,x(1)(1))模型：

GPM(1,1,x(1)(n))模型：

GPM(1,1,β)模型：

對于本文提出的初始條件和冪指數協同優化PIGPM(1，1,γ)模型，參數優化結果為：冪指數γ=0.6932，λ=0.1436，φ=7.3872，模型的預測計算公式為：

表1 4種模型的模擬值、預測值及相對誤差

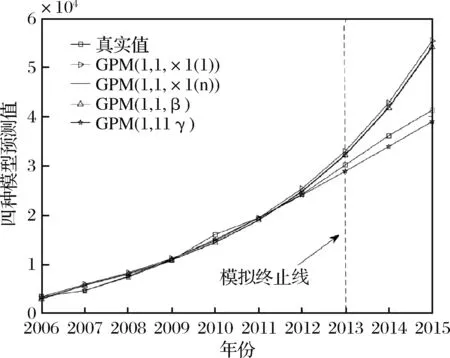
圖3 四種模型模擬和預測效果對比圖

從表1和圖3中可以看出，傳統以x(1)(1)為初始條件的GPM(1,1,x(1)(1))模型的模擬和預測誤差最大，基本已經失去預測價值，分別達到9.07%和20.64%，高于其他三種模型，主要是因為傳統模型在初始條件選取方面未考慮新信息對系統趨勢的影響，因此在預測時表現出與真實值較大的差異。對于GPM(1,1,x(1)(n))和GPM(1,1,β)模型，在引入新信息作為初始條件后，其模擬和預測精度有了一定的改善，模擬精度分別提升為8.4%和8.52%，預測精度分別提升為18.17%和17.71%，但是預測誤差還是比較大，不適合對我國網絡購物用戶規模做中長期預測分析。對于本文提出的PIGPM(1，1,γ)模型，在模擬和預測兩方面均表現出良好的適應性，精度分別取得了1.68%和5.30%，遠遠高于其他三種初始條件優化的GM(1，1)冪模型，說明本文在引入權重信息控制參數優化的初始條件具有很好的實際應用價值，充分展示了新舊信息在網絡購物用戶規模預測模型初始條件構建中的變化規律，既符合了“新信息優先原理”，又符合“信息充分利用原理”，優化的PIGPM(1，1,γ)模型適合作為我國網絡購物用戶規模的預測。

因此，基于本文提出的PIGPM(1，1,γ)的模型，對我國未來網絡購物用戶規模進行預測。借鑒新陳代謝的思想，不斷利用新數據淘汰舊數據，本文選擇7年的數據作為建模數據維度，分別預測下一年的數據，對我國2016年-2020年的網絡購物用戶規模進行建模預測。模型參數優化結果見表2，2016-2020年間每年的預測建模數據見表3，從表2和表3可以看出，對于預測我國2016-2020年網絡購物用戶規模模型模擬結果依然保持較高的精度，平均模擬誤差維持在區間[0.69%，1.55%]，因此，利用5年的預測公式對2016-2020年我國網絡購物用戶規模進行預測的可信度比較高。模型的預測計算公式為：

預測2016年網購用戶規模公式：

-29122.04)1.11297

預測2017年網購用戶規模公式：

-18798.0)1.2164

預測2018年網購用戶規模公式：

-35739.0)1.5714

預測2019年網購用戶規模公式：

-106977.0)1.0414

預測2020年網購用戶規模公式：

-200044.0)0.9924

表2 2016-2020年預測模型的參數優化值

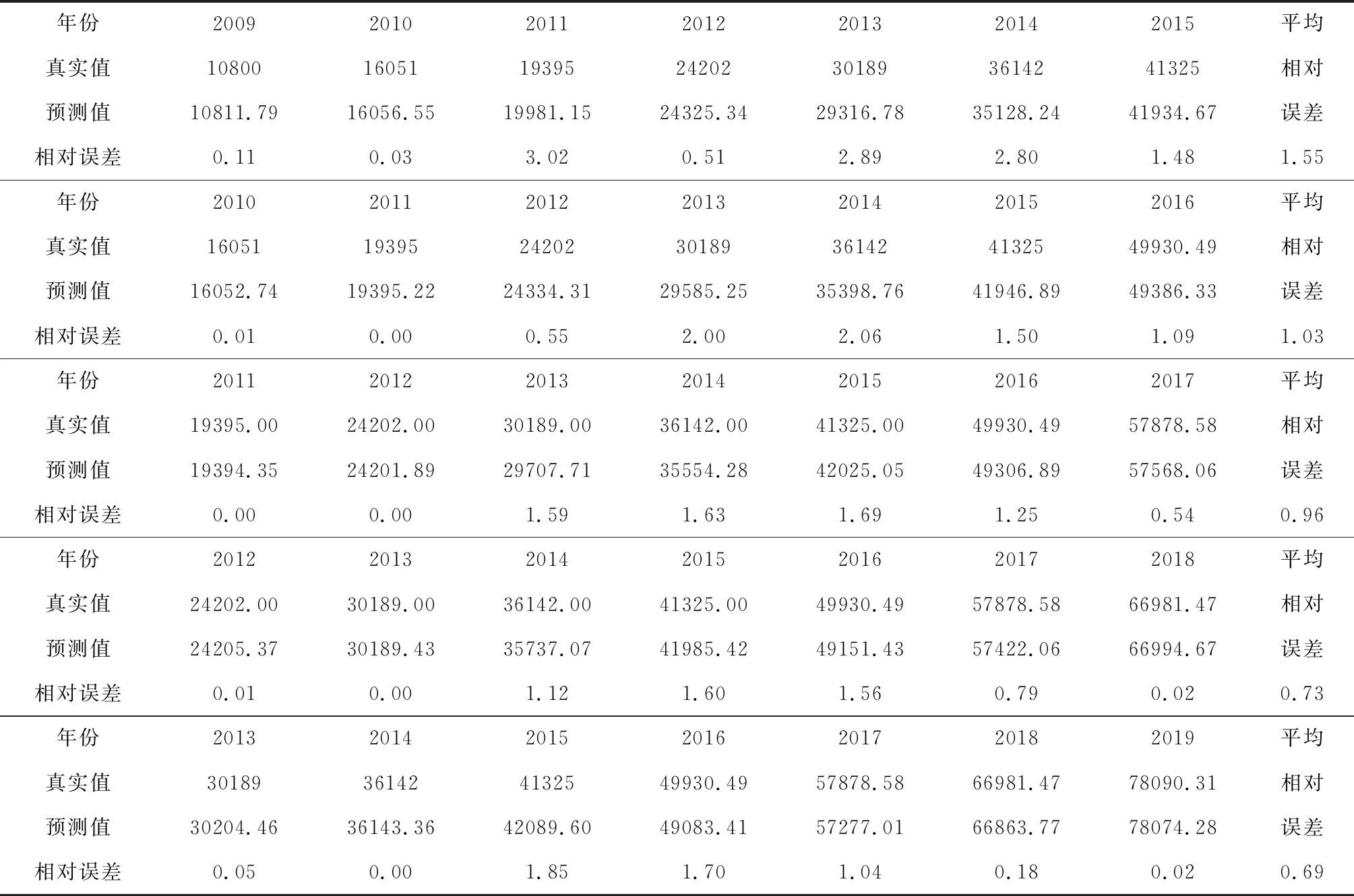
表3 我國未來網絡購物用戶規模建模數據的模擬值

為了進一步發展網上購物等電子商務的發展，我國已經從多方面展開布局，推動以拉動消費為主的經濟發展方式。在宏觀政策上，進一步完善“互聯網+”頂層設計，促進互聯網與傳統產業融合，通過電子商務培育經濟發展新動力；在發展農村電子商務方面，推動“網貨下鄉”和“農產品進城”雙向流通，從基礎設施建設、人才培養、金融支持等多方面促進農村電子商務發展，進一步釋放農村居民網絡購物消費的發展潛力；在跨境電商方面，通過降低關稅、擴大支付限額、提高通關率等政策措施，為跨境電子商務發展提供便利，進一步規范海外網購發展。從見表4可以看出，在眾多利好政策的刺激下，我國未來網絡購物將會繼續保持快速、穩健的的發展趨勢。根據中國互聯網絡信息中心發布的最新《第43次中國互聯網絡發展狀況統計報告》，2016-2018年間，我國網絡購物用戶規模分別達到46670、53332、61011(萬人)，與表4中本文模型預測的結果相比，精度分別為6.99%、8.53%和9.79%，均小于10%，達到較好的預測效果，預計到2020年我國網購用戶規模將突破9億人，可見，網上購物在未來將會成為一種消費習慣，是網民常態化的購物方式。

表4 2016-2020年我國未來網絡購物用戶規模預測值

5 結語

對于GM(1,1)冪模型，冪指數γ取值的多樣性使其能夠面向含有多種特征的序列進行預測建模，進而賦予其超越GM(1,1)模型和灰色Verhulst模型更廣闊的應用領域。然而其冪指數求解一直是困擾該模型進一步推廣應用的瓶頸，本文借助非線性優化方法和工具實現GM(1,1)冪模型的參數優化，是一種改善模型精度的有效方法。

另外，鑒于初始條件對灰色冪模型精度的重要影響，以及新舊信息在初始條件選取方面作用的差異，本文通過設計權重系數控制函數，并結合一階累加生成序列各時點數據的實際值，構造新型優化的初始條件。該新型優化的初始條件不僅能體現新信息優先原理，更能表現新舊信息作用變化規律。與此同時，利用非線性優化方法協同優化初始條件和冪指數，可以顯著地提升GM(1,1)冪模型的模擬和預測精度。

最后，在對我國網絡購物用戶規模預測實例中，本文提出的初始條件優化模型取得了較好的模擬和預測效果，并結合新陳代謝思想，對2016年-2020年的網絡購物用戶規模進行預測。通過對比常見的三種優化模型：GPM(1,1,x(1)(1))、GPM(1,1,x(1)(n))、GPM(1,1,β)，模擬和預測結果顯示，本文模型在模擬和預測階段都能表現出良好的建模效果，具有很好的適用性和穩定性。最后，采用本文優化模型對未來2016-2020年我國網絡用戶規模進行預測，通過收集2016-2018年的真實數據，對比突出本文優化模型的真實預測效果。結果顯示，本文模型在實際應用中能高精度預測未來我國網絡用戶規模的動態變化，預計2020年我國網絡購物用戶規模將會突破9億人，網上購物將會成為一種居民生活消費習慣，是網民常態化的購物方式。

單變量灰色冪模型因其特有的冪指數結構而具有對多種特征序列具有較強的適用性，未來將對其多因素影響下的多變量冪模型結構進行研究，并探討其病態性和穩定性。