加速度傳感器靈敏度計算數學模型及其求解算法

吳發明

（廈門乃爾電子有限公司，福建廈門 361000）

0 引言

壓電加速度傳感器是一種將力學量轉換為電學量的檢測裝置，可用于振動沖擊和線加速度的測量，在導彈飛行試驗和高速碰撞測試中，均要進行加速度歷程測試[1]。對于高溫應用場合的壓電加速度傳感器，由于耐溫高的客觀條件限制，高溫電荷型輸出的壓電加速度傳感器通常采用壓電元件堆棧式的軸向壓縮型結構，該傳感器結構通常在裝配成部件后，再通過機加切削調整慣性質量塊的重量，最終調整傳感器靈敏度至目標值區間內。該方式的組裝過程及靈敏度調整較為繁瑣且效率低下，此外，傳感器易因伴隨機加工產生的振動及切削熱造成慣性質量塊與壓電元件間產生相對轉動，使壓電元件存在碎裂或部件結構內部存有內應力等不良缺陷乃至報廢。為解決該問題，提高該結構型式的壓電加速度傳感器在裝配前的靈敏度計算及慣性質量塊重量調整的研究十分必要。

1 電荷靈敏度計算數學模型

由于在工程設計采取的措施和高溫應用場合的要求，壓縮型壓電式加速度傳感器結構如圖1 所示[1-2]，由基座、壓電元件、導電片、上絕緣片、下絕緣片、慣性質量塊、預緊螺母組成。當傳感器在被測物體上隨被測物運動時，其慣性質量塊在加速度的作用下產生慣性力作用在壓電元件上，壓電元件產生與此作用力成比例的變形，由于壓電元件的壓電效應，便產生與壓電元件形變成比例的電荷。

如圖1 所示，對于第i 個壓電元件而言，其慣性質量塊由質量塊、上絕緣片、（i-1）個壓電元件、（i-1）個導電片組成。故第i個壓電元件所產生的電荷靈敏度為：

因此，壓縮型壓電式加速度傳感器的靈敏度計算表達式為：

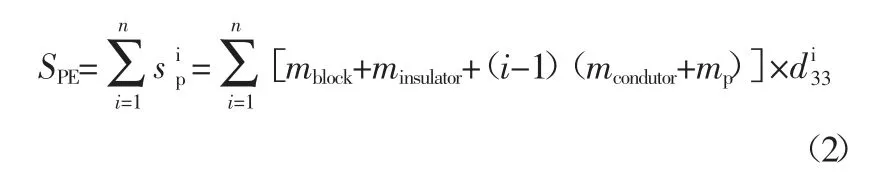
式中，mblock為慣性質量塊的質量，單位為g；minsulator為絕緣片的質量，單位為g；mcondutor為電極片的質量，單位為g；mp為壓電元件的質量，單位為為第i 個壓電元件的壓電參數，單位為pC/N。

由靈敏度計算表達式可知，實際裝配時，若將壓電參數值大的壓電元件裝配在越靠近基座，則傳感器靈敏度值越高，反之則越小。

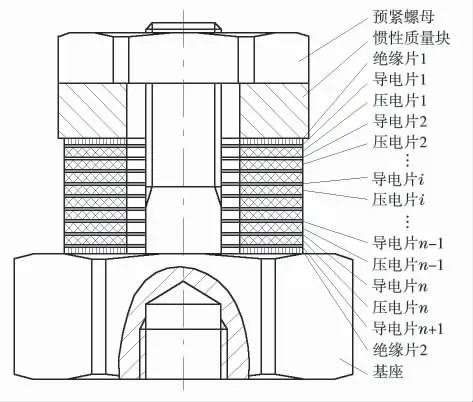
圖1 軸向堆棧式壓縮結構示意

1.1 靈敏度定義

壓縮型壓電式加速度傳感器靈敏度的數學定義可表示為：

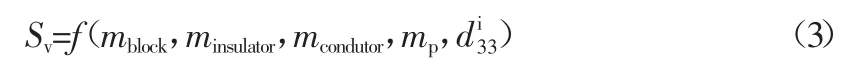
式中，mblock為慣性質量塊的質量，minsulator為絕緣片的質量，mcondutor為電極片的質量，mp為壓電元件的質量，為第i 個壓電元件的壓電系數d33。由于實際生產存在差異性，難以保證任意兩個壓電元件的壓電系數d33均相等，即，因此壓縮型結構壓電加速度傳感器所用的n 個壓電元件，存在組裝順序約束。壓縮型結構壓電加速度傳感器的靈敏度集可表示為：

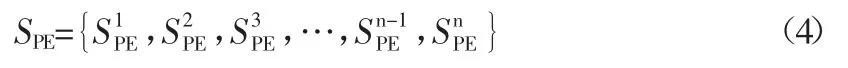
該靈敏度集的壓電元件的壓電參數序列可表示為：

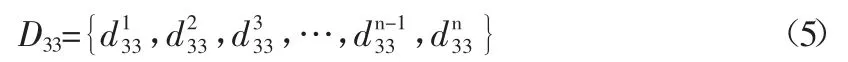
1.2 目標函數

假設某壓縮型壓電式加速度傳感器采用n 個壓電元件，其靈敏度期望值為，可接受靈敏度偏差值為。如何合理安排壓電元件的組裝順序，使傳感器靈敏度最接近其期望值即為靈敏度最優求解問題，則靈敏度集Sv尋優的數學模型為：

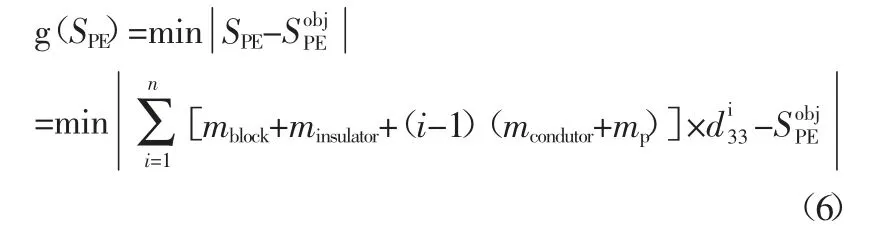
1.3 評價函數

為衡量算法迭代新解的優化程度，給定第i 次迭代計算評價函數的數學定義為：

式中，Δgi稱為第i 次迭代的函數代價差，為第i 次迭代的初始解為第i 次迭代的新解，g（SPE）為SPE的代價函數。若Δgi＜0 或滿足Metropolis 概率接受準則[3]，則稱新解優于初始解

1.4 最優求解

由式（6）可知，傳感器靈敏度最優求解問題的主要因素為壓電元件的壓電參數序列D33和慣性質量塊質量mblock的尋優問題。

基于初始質量塊的質量mblock，求解得到壓電元件的壓電參數迭代最優序列，其對應的靈敏度為則壓電參數迭代最優序列作為最終最優序列輸出；否則，基于壓電參數迭代最優序列求解得到慣性質量塊的質量

2 算法

2.1 算法流程

對于壓電元件數量較多的壓縮型壓電式加速度傳感器靈敏度規劃問題，若采用窮舉法求解，則計算量隨壓電元件個數n 呈指數級增長，耗時長且計算效率低。由于模擬退火算法具有全局最優的理論特性[4]，本文采用混沌模擬退火算法求解壓縮型壓電式加速度傳感器靈敏度最優規劃數學模型，收斂到全局最優解的效率明顯比標準模擬退火算法高。

混沌模擬退火算法流程如圖2 所示[5]，該算法相比標準模擬退火算法，增加了記憶當前最優解的功能、補充了回火升溫過程并引入混沌隨機序列生成函數，其中：①定義及初始化。定義并初始化冷卻進度參數（退火起始溫度ts及終止溫度te、冷卻系數Q 和MapKob 鏈長MapKobL）、玻爾茲曼常數kB、回火系數At以及新解的接受次數AccecptNum，并選定初始迭代解；②對當前t 和i=1，2，…，MapKobL，重復執行③～⑤；③對當前解混沌隨機產生新解；④計算函數代價差Δgi；⑤若Δgi＜0，則接受為（i+1）次迭代的初始解；否則計算Metropolis 概率值Accept（Δgi，t）=exp（-Δgi/1.5t），并在閉區間［0，1］上混沌產生隨機數randVal，若滿足Accept（Δgi，t）＞randVal，則否則⑥在次迭代之后，若新解的接受次數AcceptNum 大于預設值，則退火降溫；否則回火升溫，重新執行②～⑤；⑦若滿足迭代終止條件，則輸出迭代最優解；否則返回②，繼續迭代計算。本文的迭代終止條件為連續3×MapKobl 個迭代新解未被接受或當前溫度t≤te；⑧若迭代最優解滿足期望偏差條件，則輸出壓電元件的參數序列迭代最優解，結束程序；否則基于壓電元件的參數序列迭代最優解，求解得到慣性質量塊的質量，結束程序。

2.2 控制參數

基于混沌模型具有遍歷性、初值條件敏感性等特點[6]，本文采用一維Logistic 映射的常用混沌模型作為混沌隨機序列的生成函數，其數學模型[6]為：

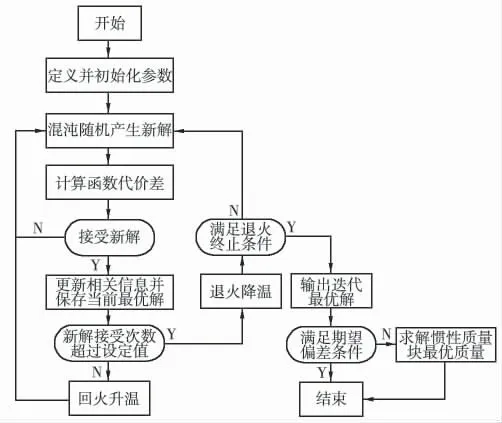
圖2 算法流程

其中x∈［0，1］，μ∈［0，4］，為混沌控制參數。當μ=4，該系統無穩定解，是區間的滿映射，呈現完全混沌狀態。因此，本文取μ=4。

相關控制參數的具體取值如表1 所示，取值說明：①退火起始溫度ts及退火終止溫度te。以退火溫度t 為混沌隨機序列生成的迭代初值，因此t∈［0，1］，結合退火過程的充分性及計算效率而確定具體取值；②冷卻系數Q。本文采用指數式降溫，結合熱力學退火過程，為豐富系數Q 的取值、增強算法的適應性并提高迭代計算速度而確定Q 在各個溫度區間內的具體取值；③MapKob鏈長MapKobL。增加算法自適應性，充分退火并提高收斂到全局最優解的可靠程度而確定其具體取值；④波爾茲曼常數kB。依據Metropolis 概率接受準則，提高算法避免陷入局部最優的能力而確定其具體取值；⑤回火系數At。統籌兼顧計算速度及退火充分程度的影響而設定此參數值；⑥新解的接受次數AcceptNum。結合退火充分程度及迭代解優化程度而設定具體取值。

3 算例驗證

3.1 測試實例

如圖1 所示的軸向堆棧式壓縮結構，實際驗證的傳感器由1 個預緊螺母，1 個質量塊，2 個絕緣片，12 個導電片，13 個壓電元件和1 個基座組成，具體參數見表2。由此可見，對于壓電元件數量較多的壓縮型傳感器，若采用人工交互方式規劃壓電元件的裝配順序，效率低且易出錯。

表1 算法參數

3.2 驗證結果

以VB 語言編寫實現，進行30 次實例測試。測試用的電腦配置為雙核，CPU 主頻3.30 GHz，內存8 GB。針對壓縮型傳感器壓電元件的壓電參數序列以D33={20.6，20.1，20.7，20.5，10.2，20.4，10.8，20.2，20.8，10.4，20.3，20.9，10.6}作為初始序列，則初始靈敏度值為67.82 Pc/g。30 次測試的迭代計算結果統計內容包括最大靈敏度最小靈敏度如表3 所示。其中對應的壓電元件的壓電參數序列={10.2，10.4，10.6，10.8，20.1，20.2，20.3，20.4，20.5，20.6，20.7，20.8，20.9}對應的壓電元件的壓電參數序列={20.9，20.8，20.7，20.6，20.5，20.4，20.3，20.2，20.1，10.8，10.6，10.4，10.2}。

表2 傳感器參數

由表3 計算結果可知，基于當前的壓電元件的壓電參數序列D33，必須調整慣性質量塊的質量方能確保組裝后所得的靈敏度滿足其期望值及其偏差的要求。慣性質量塊的質量調整區間為［20.16，21.90］。

由以上實例驗證結果可知，構建的壓縮型壓電式加速度傳感器靈敏度優化規劃數學模型及其求解算法，在傳感器靈敏度尋優時，具有計算用時少、自動化水平高的特點，優化所得的壓電元件裝配序列及靈敏度計算結果令人滿意，可應用于堆棧式壓縮型結構的壓電式加速度傳感器的實際組裝生產指導。

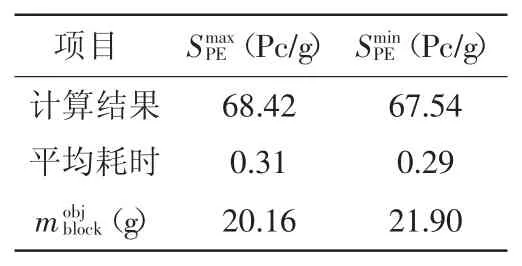
表3 測試結果

4 結論

通過壓縮型壓電式加速度傳感器靈敏度規劃的數學模型及其求解算法，建立壓縮型PE 加速度傳感器靈敏度自動優化方法。通過實例驗證結果，表明該方法可解決壓縮型壓電式加速度傳感器組裝過程及靈敏度調整較為繁瑣費時且效率低的問題。該自動優化方法與實際裝配后再通過車削質量塊進行減重的傳統方法相比，可滿足實際裝配工藝需求，且具有效率高、尋優質量穩定、可提前預警等優點。